系列文章目录
- leetcode - 双指针问题_leetcode双指针题目-优快云博客
- leetcode - 滑动窗口问题集_leetcode 滑动窗口-优快云博客
- 高效掌握二分查找:从基础到进阶-优快云博客
- leetcode - 前缀和_前缀和的题目-优快云博客
- 动态规划 - 斐波那契数列模型-优快云博客
- 位运算 #常见位运算总结 #题解-优快云博客
- 模拟 - #介绍 #题解-优快云博客
- leetcode - 分治-三路划分快速排序总结-优快云博客
- 动态规划 - 路径问题-优快云博客
目录
前言
路漫漫其修远兮、吾将上下而求索;
大家可以自己先尝试做一下~
- 面试题 17.16. 按摩师 - 力扣(LeetCode)
- 213. 打家劫舍 II - 力扣(LeetCode)
- 740. 删除并获得点数 - 力扣(LeetCode)
- LCR 091. 粉刷房子 - 力扣(LeetCode)
- 309. 买卖股票的最佳时机含冷冻期 - 力扣(LeetCode)
- 714. 买卖股票的最佳时机含手续费 - 力扣(LeetCode)
- 123. 买卖股票的最佳时机 III - 力扣(LeetCode)
- 188. 买卖股票的最佳时机 IV - 力扣(LeetCode)
1、题1 按摩师 :
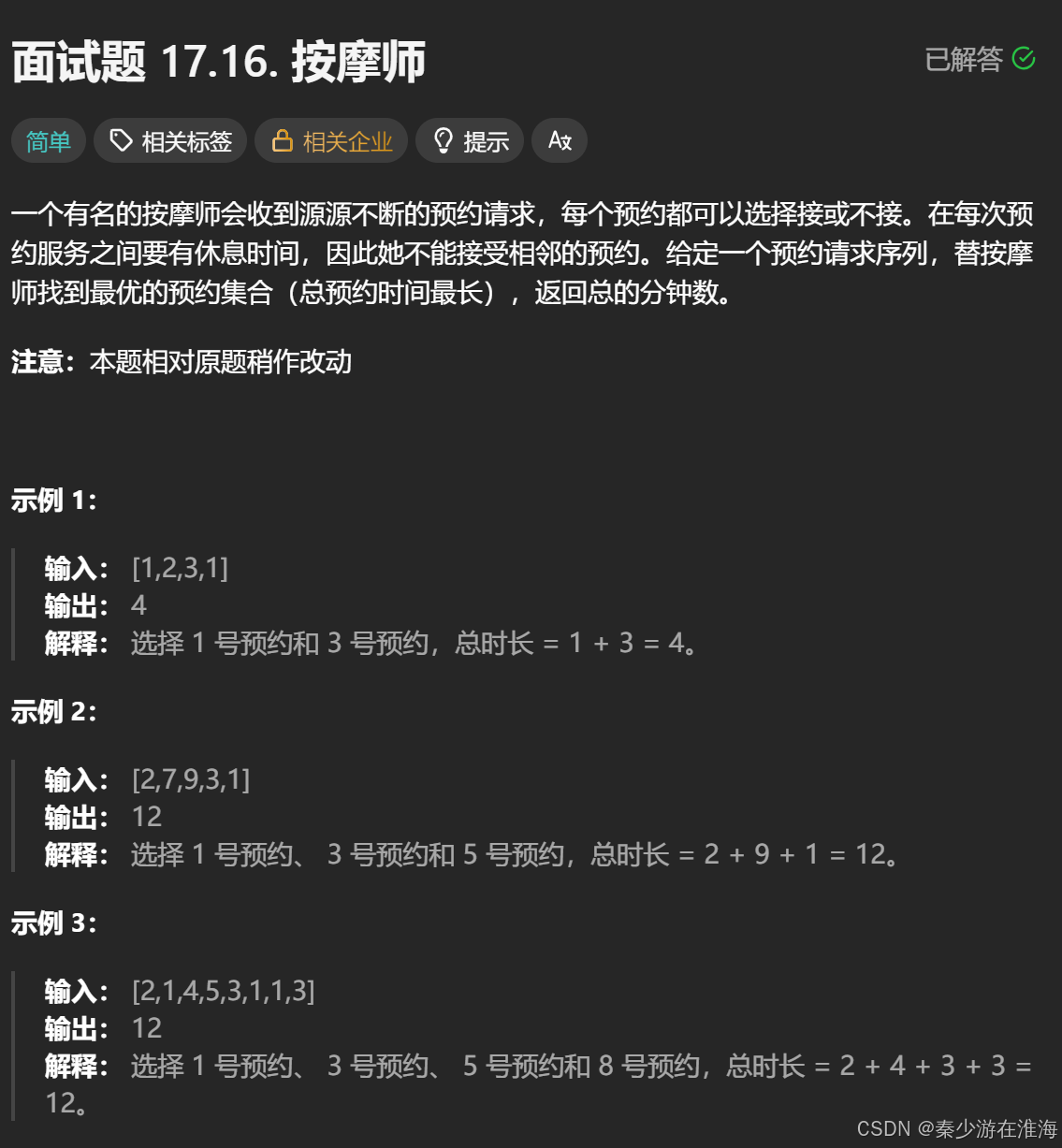
梳理:每一个预约有两种处理方式:接、不接;要求,预约时间不相邻;求最长预约时长;
同样地,动态规划问题需要分五步进行解决:
1、确定状态表示 2、状态转移方程 3、初始化 4、填表顺序 5、返回值
1.1 确定状态表示
确定状态表示一般是以某一个位置为开始,或者以某一个位置为结尾;
dp[i] 表示:选择到 i 位置的时候,此时的最长预约时间;
但本题的问题有一点特殊,关于本题的状态表示还可以划分成两个更细的子状态:当选到 i 位置可以分为两种情况:1、选为 i 位置的值; 2、不选择 i 位置的值;
我们可以将这两种细分的状态表现为两个dp 表:f[i] 表示选,g[i] 表示不选;还有一种处理方式:创建一个行数为2的二维dp表,dp[0][i] 表示i位置选,dp[1][i]表示 i 位置不选:
(此处创建两个dp 表来解决:)

1.2 状态转移方程
- 对于 f[i] , 走到 i 位置,i 位置是必选的;而当 第 i 个位置选了的时候,由于相邻位置不能选,那么 i-1 位置一定不能被选,而我们此时需要得到的是 [0,i-2] 区间中 最长的预约时长,怎么得到呢?g[i-1] 代表着 i-1 位置不选时的最长预约时长,也就是说 g[i-1] 中存储着 [0,i-2] 区间中的最长预约时长;而当前 i 位置是必选的,所以 f[i] = g[i-1] + nums[i];
- 对于 g[i] ,走到 i 位置, i 位置是不选的;而当第 i 个位置不选的时候,其前一个位置 i-1 可选可不选;我们需要得到 [0,i-1] 区间中的最长预约时长,而i-1 位置上的数据可选可不选,选即f[i-1] 不选即 g[i-1] ,求这二者的最大值即可;所以 g[i] = max(f[i-1] , g[i-1] );
1.3 初始化
初始化的目的就是为了避免在填表的时候发生越界问题,观察我们的状态转移方程: f[i] = g[i-1] + nums[i];以及 g[i] = max(f[i-1] , g[i-1] ); 均用到了 下标 i-1 的数据,而当 i 为0 时候,下标就不合法了,所以我们需要初始化 f[0] 与 g[0] ;
- f[0] 表示第0 个位置选了的时候其最大预约时长,即 f[0] = nums[0];
- g[0] 表示第0 个位置不选的时候其最大的预约时长,即 g[0] = 0;
1.4 填表顺序
我们填表的时候,需要确保自己在填当前位置的时候所要依靠前面的状态是已知的;由于我们的状态转移方程依靠与前面的状态,并且,两个dp 表互相影响;所以填表顺序为:两个dp表同时从左往右进行填表;
1.5 返回值
题干求的是整体的最长的预约时长;到了最后一个位置仍然也有两种情况,我们求最大值即可;
假设一共有 n 个预约,那么返回值为 max(f[n-1] , g[n-1]);
参考代码:
int massage(vector<int>& nums)
{
int n = nums.size();
//边界情况处理
if(n==0) return 0;
vector<int> f(n) , g(n);//f[i]:选 i 时的最长预约时长 g[i]:不选i 时的最长预约时长
//初始化
f[0] = nums[0] , g[0] = 0;
//填表
for(int i = 1;i<n;i++)
{
//两个dp 表同时填
f[i] = g[i-1] + nums[i];
g[i] = max(f[i-1] , g[i-1]);
}
//返回
return max(f[n-1] , g[n-1]);
}2、题2 打家劫舍 II :

梳理:不能偷连续的房子,求小偷偷得得最大金额;
本题的首尾是相接的,即偷了第一家就不能偷最后一家,而偷了最后一家就不能偷第一家;需要分情况讨论,转换题意:
将第一个位置分为两种情况:第一个位置要偷;第一个位置不偷;
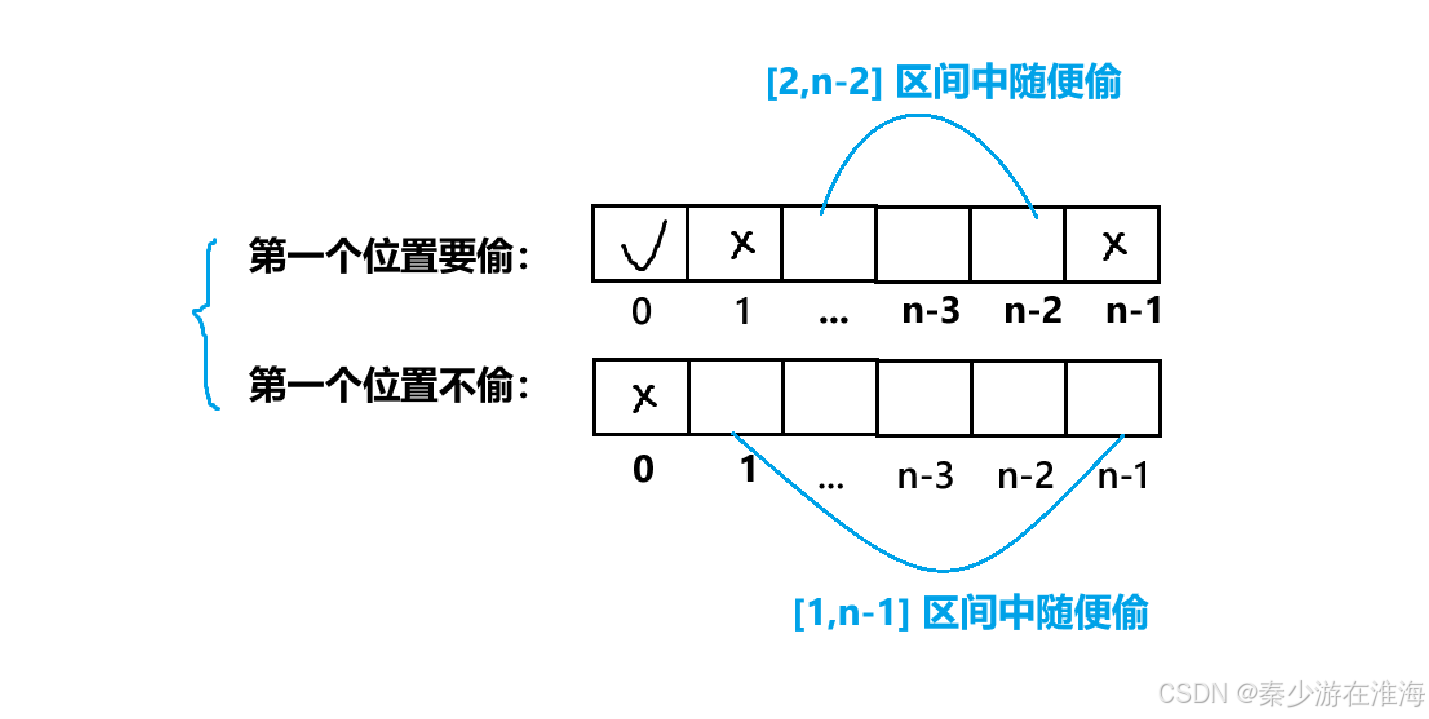
假设我们求在某一个区间中偷得钱得最大值的函数为 rob;
那么:
- 第一个位置要偷的时候,其最大值为:nums[0] + rob(2,n-2);
- 第一个位置不偷的时候,其最大值为: rob(1,n-1);
而最终的结果就是这两种情况中的最大值;
通过这样分类讨论的处理,可以将环形的问题,转换成两个线性的“打家劫舍”;
2.1 确定状态表示
状态表示的确定一般是以某一个位置为结尾,或者是以某一个位置为起点;
根据题意,相邻的房子不能偷,而一个位置有两种情况:偷或者不偷;此处我们也得用到两个dp表,或者创建二维dp表来解决;
创建两个dp表:
- f[i] 表示:偷到 i 位置时,偷 nums[i] ,此时的最大金额
- g[i] 表示:偷到 i 位置时,不偷nums[i] ,此时的最大金额;
2.2 状态转移方程
- 对于 f[i], 走到第 i 间房子,必须偷;那么第 i-1 个房子就一定不会被偷,而此时需要得到 [0,i-2] 中的最大值,显然就是 g[i-1] ;所以 f[i] = g[i-1] + nums[i];
- 对于 g[i] , 走到第 i 间房子,可以偷可以不偷,此时就有两种情况,取最大值即可;即 g[i] = max(f[i-1] , g[i-1]);
2.3 初始化
观察我们的状态转移方程:f[i] = g[i-1] + nums[i];以及 g[i] = max(f[i-1] , g[i-1]); 发现,当i 为0 的时候其下标就不合法,所以需要初始化 g[0] 、f[0] ;
- 对于f[0] ,走到第 i 间房子的时候,偷,即 f[0] = nums[0];
- 对于 g[0] , 走到第 i 间房子的时候,不偷,即 g[0] = 0;
2.4 填表顺序
关注填表顺序是为了保障在填表的时候所要依靠的状态已经存在,通过对状态转移方程的分析,我们可以得知,当我们填第 i 位置的数据时依靠其前一个状态,并且两个dp 表相互影响;所以在填表的时候,两个表需要一起从左往右填表;
2.5 返回值
返回两个表中的最大值,即 max(f[n-1] , g[n-1]);
参考代码:
int robhome(vector<int>& nums , int left , int right)
{
//范围合法
if(left > right) return 0;
int n = nums.size();
vector<int> f(n),g(n);
//初始化
f[left] = nums[left] , g[left] = 0;
//填表
for(int i = left+1;i<=right;i++)
{
//同时填表
f[i] = nums[i] + g[i-1];
g[i] = max(f[i-1] , g[i-1]);
}
return max(g[right] , f[right]);
}
int rob(vector<int>& nums)
{
//分两种情况
int n = nums.size();
//第一个房间偷-> nums[0] + robhome(2,n-2) 不偷--> robhome(1,n-1) 取这两种情况的最大值
return max(nums[0]+robhome(nums,2,n-2) , robhome(nums,1,n-1));
}3、题3 删除并获得点数:
梳理:从nums 中选一个数据 x ,但是之后就不能选 x-1 或者 x+1 ;
我们需要先处理一些本题,若数据是有序的,那么本题就相当于是“打家劫舍”的问题,就不能选被选数相邻的数;但还有一个点:所给的数据之间会有断层,处理好“断层”的这个问题才能用“打家劫舍”的思想来解决;
Q:如何处理断层问题?
- 再利用一个数组 arr , 用下标来表示该nums 中的数据;而arr 数组中的空间存储该数据出现的总和,如下:

arr[i] 表示 i 这个数据出现的总和;
那么接下来在 arr 数组中做一次”打家劫舍“问题即可;
3.1 确定状态转移方程
状态转移方程的确定,要么是以某一个位置为结尾,要么是以某一个位置为结束;
根据我们的经验以及题干要求来确定状态转移方程;
当我们走到 i 位置的时候,该数可选可不选,有两种状态,所以此处我们需要用到两个dp 表是,或是用二维dp 解决;
- f[i]: 走到 i 位置时,i 中的位置必选,此时能获得的最大点数;
- g[i]: 走到 i 位置时,i 中位置不选,此时能获得的最大点数;
3.2 状态转移方程
- 对于 f[i] , 走到 i 位置的时候, i 位置上的数据必选,那么 i-1 位置上的数据一定不能选,想要得到走到 i 位置时能获得的最大点数,首先就要先获得[0,i-2] 中能获得的最大点数,即 g[i-1] ;所以 f[i] = g[i-1] + arr[i];
- 对于 g[i] 来说,走到 i 位置的时候, i 位置上的数据一定不能被选,那么 i-1 的位置上可选可以不选,求得这两种情况的最大值即可;即 g[i] = max(f[i-1] , g[i-1]);
3.3 初始化
初始化的目的是为了在填表的过程中下标合法,不会发生越界访问;观察我们的状态转移方程可以得知,当 i 为0 的时候,下标就不合法了;所以我们应当初始化 f[0] 以及 g[0];
- 而f[0] ,代表走带下标为0 的位置,必选,那么 f[0] = arr[0];
- 而g[0], 代表走到下标为0的位置,不选,那么 g[0] = 0;
3.4 填表顺序
确定填表书顺序是为了保证我们在填表的时候,当前所填值所依靠的状态是已知的;而我们的两个dp表还相互影响,所以我们的填表顺序:两个dp表同时从左往右填表;
3.5 返回值
返回 f[n-1] 与 g[n-1] 中给的最大值即可;
参考代码1:
int deleteAndEarn(vector<int>& nums)
{
int n = nums.size();
//先处理数据
int maxi = INT_MIN;
for(auto e:nums) if(e>maxi) maxi = e;
vector<int> arr(maxi+1);
for(auto e: nums)
{
arr[e]+=e;
}
vector<int> f(maxi+1) , g(maxi+1);
//初始化
f[0] = arr[0] , g[0] = 0;
//填表
for(int i = 1; i<=maxi;i++)
{
//两个表同时填
f[i] = g[i-1] + arr[i];
g[i] = max(f[i-1] , g[i-1]);
}
return max(f[maxi] , g[maxi]);
}也可以不找nums 中的最大值开辟空间,直接粗暴点还可以根据数据范围创建arr数组:
粗暴点的做法:直接创建大小为10001的arr 数组:
参考代码2:
int deleteAndEarn(vector<int>& nums)
{
const int N = 10001;
int arr[N] = {0};
for(auto e:nums) arr[e]+=e;
vector<int> f(N) , g(N);
//初始化
f[0] = arr[0] , g[0] = 0;
//填表
for(int i = 1; i<N;i++)
{
//两个表同时填
f[i] = g[i-1] + arr[i];
g[i] = max(f[i-1] , g[i-1]);
}
return max(f[N-1] , g[N-1]);
}4、题4 粉刷房子 :
梳理:有一排房子,每个房子刷不同颜色的漆价格不同,并且相邻的房子的颜色不能相同;求将房子全部粉刷完的最小花费;
4.1 确定状态表达式
我们的状态表达式要么是以某一个位置为结尾,要么是以某一个位置为开头;
根据我们的经验以及题目要求:
dp[i] 表示到达 i 位置的时候的最小花费;但是由于到达 i 位置有三种情况(三种颜色可选),所以我们的状态表达式还需要继续细分,我们可以使用三个dp表,或者是创建二维dp表,由于本题中数据给的是二维数组,我们此处最好也是创建一个二维dp表;
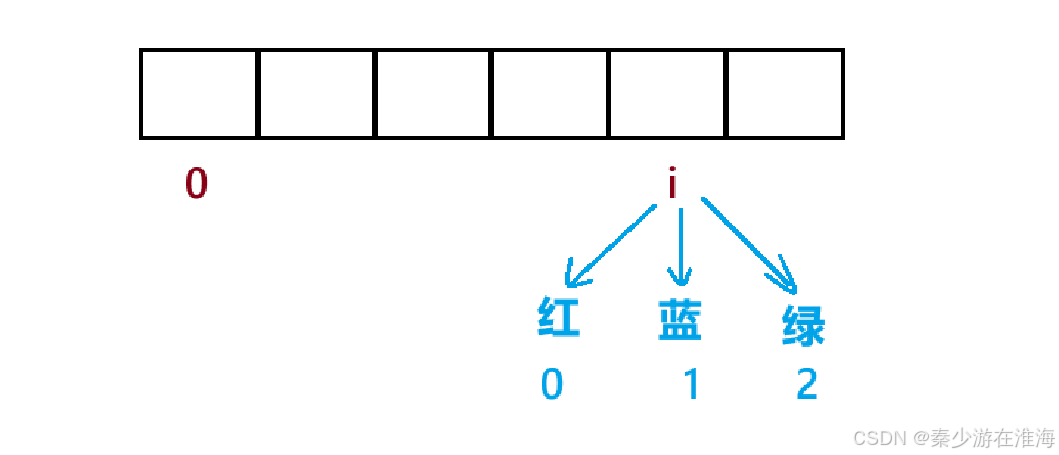
- dp[i][0] 表示:粉刷到 i 位置的时候,该位置上红色,此时的最小花费;
- dp[i][1] 表示:粉刷到 i 位置的时候,该位置上蓝色,此时的最小花费;
- dp[i][2] 表示:粉刷到 i 位置的时候,该位置上绿色,此时的最小花费;
4.2 推导状态转移方程
对于dp[i][0] ,走到第 i 个位置,将第 i 个位置上的房子粉刷成红色,那么第 i-1 个房子一定是蓝色或者绿色,求这两种情况花费的最小值即可;即 dp[i][0] = min(dp[i-1][1] , dp[i-1][2]) + cost[i][0];
同理可得:
dp[i][1] = min(dp[i-1][0] , dp[i-1][2] ) + cost[i][1];
dp[i][2] = min(dp[i-1][0] , dp[i-1][1] ) + cost[i][2];
4.3 初始化
初始化的目的是为了确保在填表的时候不会发生越界的情况,通过观察状态转移方程可以得知,当i 等于0的时候,下标会不合法,所以我们需要初始化 dp表的第一行;
- dp[0][0] : 表示下标为0的房子粉刷红色,所以dp[0][0] = cost[0][0];
- dp[0][1] : 表示下标为0的房子粉刷为蓝色,所以dp[0][1] = cost[0][1];
- dp[0][2] :表示下标为0的房子粉刷为绿色,所以 dp[0][2] = cost[0][2];
当然,此处还有一种处理方式,为dp 表多开辟一行,并且保证虚拟节点里面的值不会影响后续填表的正确性,以及下标的映射关系;
实际上我们手动初始化的逻辑是与填表的逻辑相重的,所以此处更推荐为dp表多开辟一行,且虚拟结点中的值为0,这种处理方式;
4.4 填表顺序
从左往右进行填表,一次填3个表
4.5 返回值
返回值这三个表中最后一种状态的最小值即可;
- 倘若多开辟了一行,那么返回 min(dp[n][0],dp[n][1] ,dp[n][2]);
- 倘若没有多开辟一行,全靠手动初始化,即返回min(dp[n-1][0],dp[n-1][1] ,dp[n-1][2]);
参考代码:
int minCost(vector<vector<int>>& costs)
{
int n = costs.size();
vector<vector<int>> dp(n+1,vector<int>(3));//多开辟一行
for(int i = 1;i<=n;i++)
{
//三个dp表同时填写
//注意下标的映射关系
dp[i][0] = min(dp[i-1][1] , dp[i-1][2]) + costs[i-1][0];
dp[i][1] = min(dp[i-1][0] , dp[i-1][2]) + costs[i-1][1];
dp[i][2] = min(dp[i-1][0] , dp[i-1][1]) + costs[i-1][2];
}
return min(dp[n][0] , min(dp[n][1] , dp[n][2]));
}5、题5 买卖股票的最佳时机含冷冻期:
309. 买卖股票的最佳时机含冷冻期 - 力扣(LeetCode)
梳理:卖出股票之后,第二天无法买入;求买卖股票的最大利润;
5.1 确定状态表示
状态表示一般都是以某一个位置为结束或者以某一个位置为开始;
像这种从左向右的模型,一般是根据经验+ 题目要求来解决的;
先尝试以某一个位置为结尾:dp[i] 表示在第 i 天结束时此时的最大利润;而在第 i 天,其实有三种状态:买入状态、冷冻状态、可交易状态(卖出了,并且不处于冷冻期),介于此处有三种状态需要用到三个状态表示;
我们可以创建3个数组(3个dp数组)或者是创建二维数组来解决;此处选择创建二维数组;
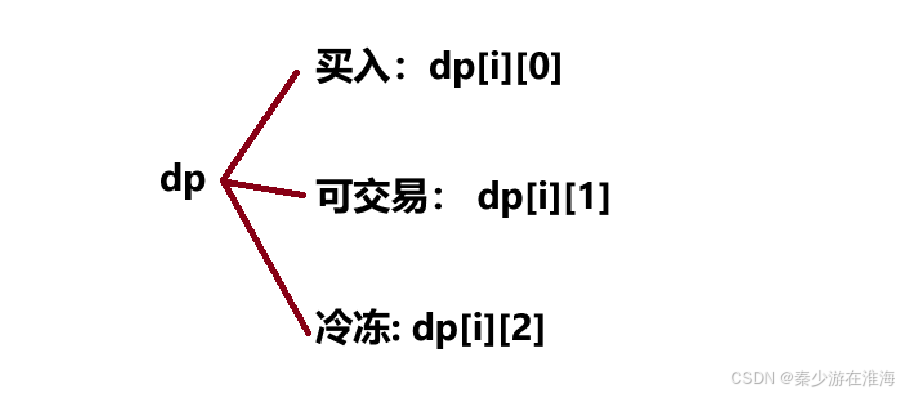
那么:
- dp[i][0] : 第 i 天结束之后,处于"买入" 状态,此时的最大利润
- dp[i][1] : 第 i 天结束之后,处于 "可交易" 状态,此时的最大利润
- dp[i][2] : 第 i 天结束之后,处于 “冷冻" 状态,此时的最大利润
5.2 状态转移方程
Q: 在第 i 天结束时,如何才能处于买入状态?
- 先看第 i-1 天的情况,然后再结合当天的情况才可以判断第 i 天结束是否可以进入买入状态;分析如下:
- 如果第 i-1 天结束之后为“买入”,那么第 i 天可以啥也不干,此时第 i 天结束依旧处于买入状态 --> dp[i][0] = dp[i-1][0];
- 如果第 i-1 天结束之后为"冷冻期" , 而冷冻期这一天不可以买入,所以第 i 天不可以买入股票,即第i天前一天一定不是“冷冻期”;
- 如果第 i-1 天结束之后为"可交易" , 那么在第 i 可以买入,那么第 i 天结束之后就为买入状态 --> dp[i][0] = dp[i-1][0] - prices[i];
对于“可交易”、“冷冻期”的分析同理可得:
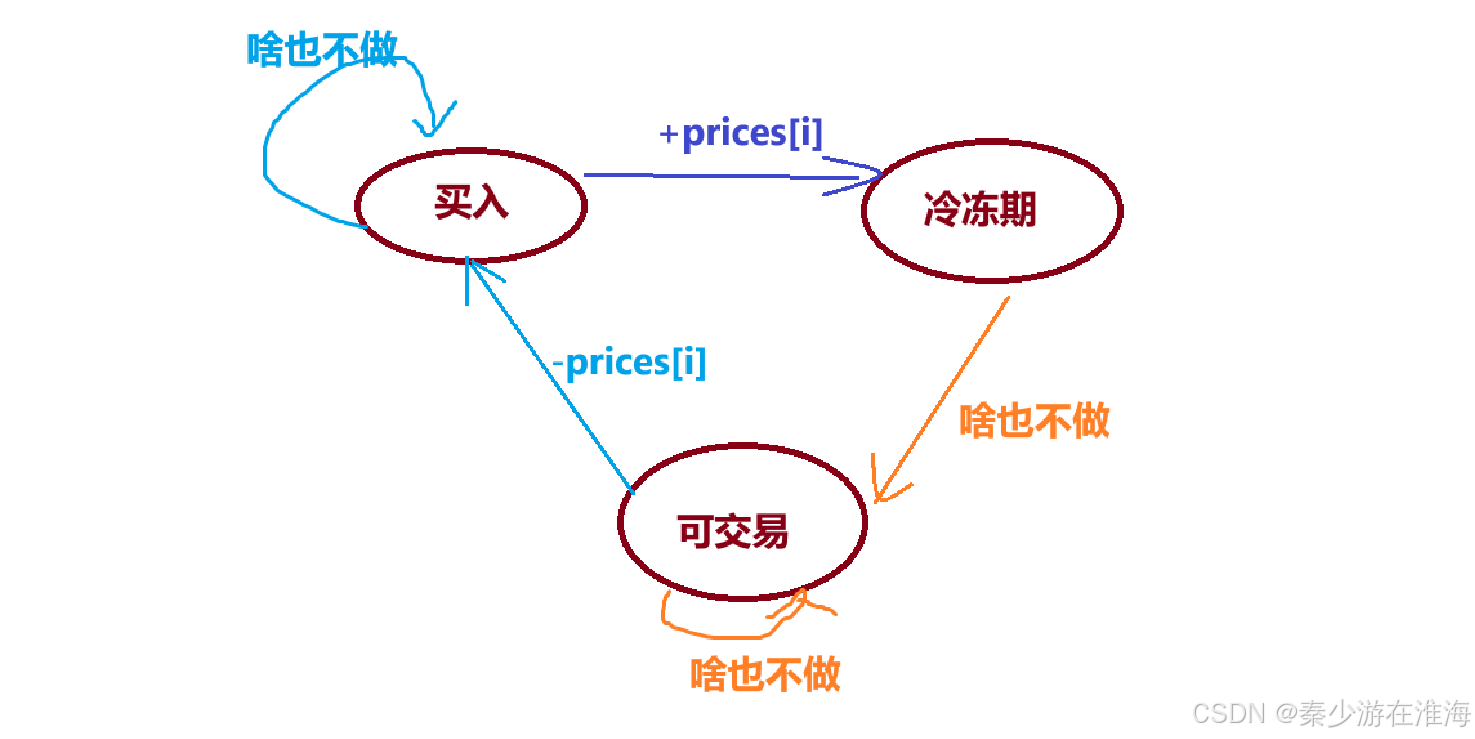
需要注意的是,箭头起始的位置指的是前一天结束得状态,箭头所指得是当天结束得状态;
那么状态转移方程如下:
dp[i][0] = max(dp[i-1][0] , dp[i-1][1] - prices[i]);
dp[i][1] = max(dp[i-1][1] , dp[i-1][2]);
dp[i][2] = dp[i-1][0] + prices[i];
5.3 初始化
通过观察我们得状态转移方程,我们可以发现当 i 为0 的时候,下标不合法;所以为了避免越界访问,我们首先会将第一行的数据进行初始化, 即 对 dp[0[0] 、dp[0][1] 、dp[0][2] 进行初始化;
dp[0][0]: 买入状态,dp[0][0] = -prices[0]
dp[0][1]:可交易状态, dp[0][1] = 0;
dp[0][2] : 冷冻状态, dp[0][2] = 0;
5.4 填表顺序
因为着三个dp 表相互牵制,所以我们必须一行一行的填表,并且需要先填上面的再填下面的,即填表顺序为:从左往右、三个表同时填写;
5.5 返回值
结合题意:![]()
而最后一天结束之后会有三个状态,暴力一点的就是直接返回最后一天结束的时候三个状态中利润的最大值即可;但,我们还可以稍微分析一下,当最后一天结束后的最大利润状态,一定不会是“买入”状态(因为会有花销),所以只需要在 “可交易”状态与“冷冻”状态中取较大值;
即返回值为:max(dp[n-1][1],dp[n-1][2]):
参考代码:
int maxProfit(vector<int>& prices)
{
int n = prices.size();
vector<vector<int>> dp(n,vector<int>(3));//dp[i][0]:买入; dp[i][1]:可交易; dp[i][2]:冷冻
//初始化
dp[0][0] = -prices[0],dp[0][1] = 0 , dp[0][2] = 0;
//填表
for(int i = 1; i<n;i++)
{
for(int j = 0; j<3;j++)
{
//三个表一起填
dp[i][0] = max(dp[i-1][0] , dp[i-1][1] - prices[i]);//买入
dp[i][1] = max(dp[i-1][1] , dp[i-1][2]);//可交易
dp[i][2] = dp[i-1][0] + prices[i];//冷冻
}
}
//最后一天结束时利润最大一定不是买入状态,返回可交易 与 冷冻状态中的最大值即可
return max(dp[n-1][1] , dp[n-1][2]);
}6、题6 买卖股票的最佳时机含手续费 :
714. 买卖股票的最佳时机含手续费 - 力扣(LeetCode)
梳理:交易需要支付手续费用,只能持有一张股票;
6.1 确定状态表达式
本题与上一题类似;
假设 dp[i] 为第 i 天结束之后的最大利润,那么第 i 天就有两种状态:买入、卖出;所以需要两个状态表达式;
可以创建两个单独的数组充当两个dp表,也可以是创建一个二维数组来充当dp 表;这两种方式均可以,介于上一题中使用的是二维数组充当dp 表,那么此处就换一种形式,使用两个到单独的数组来充当 dp 表;
那么状态表示:
f[i]表示:第 i 天结束后,处于 "买入"状态,此时的最大利润;
g[i] 表示:第 i 天结束后,处于 "卖出"状态此时的最大利润;
6.2 推导状态转移方程
需要注意的是,本题之中每完成一个交易均是需要缴纳手续费用的,我们可以在买入的时候交手续费,也可以在卖出的时候交手续费,这两种情况均是可以的;此处的解析中采用在"卖出"的时候交手续费:
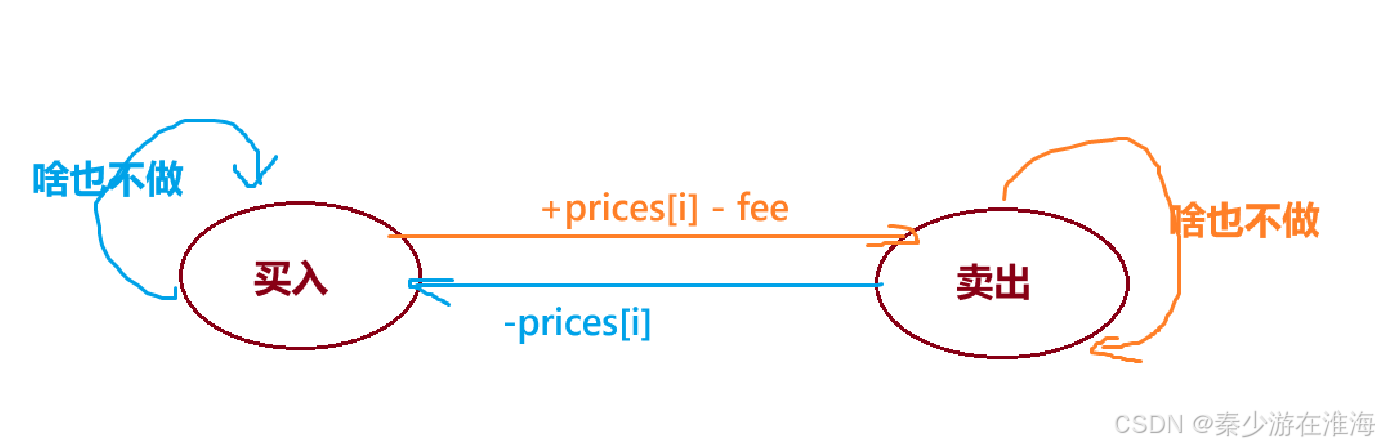
那么状态转移方程:
f[i] = max(f[i-1] , g[i-1]-prices[i]):
g[i] = max(g[i-1] , f[i-1]+prices[i]-fee);
6.3 初始化
观察状态转移方程可以发现,当 i 为0 的时候,下标会发成越界访问;所以我们需要初始化 f[0] 与 g[0];
f[0] : "买入",f[0] - -prices[i]
g[0] : “卖出”, g[0] = 0;
6.4 填表顺序
因为这两个dp 表相互影响,所以这两个dp 表需要同时填表;并且因所填状态依靠前一个状态的值,所以需要从左往右进行填表;
6.5 返回值
结合题意:![]()
返回 max(f[n-1], g[n-1]) 即可;
参考代码:
int maxProfit(vector<int>& prices, int fee)
{
int n = prices.size();
vector<int> f(n), g(n);//f[i] : 买入; g[i]:卖出
//初始化
f[0] = - prices[0] ,g[0] = 0;
//填表
for(int i = 1; i< n;i++)
{
//两个表一起填写
f[i] = max(f[i-1] , g[i-1]-prices[i]);
g[i] = max(g[i-1] , f[i-1]+prices[i] - fee);
}
return max(f[n-1] , g[n-1]);
}7、题7 买卖股票的最佳时机 II:
123. 买卖股票的最佳时机 III - 力扣(LeetCode)
梳理:不能同时参与多笔交易,但是最多只能完成两笔交易,求能获取的最大利润;
需要注意的是,我们最多只能完成两笔交易并不意味着我们只能完成两笔交易,我们可以不交易,当股票的价格一直在跌的时候,我们此时不买,最大的利润为0;我们也可只交易一笔;即我们的可交易数:0笔、1笔、2笔
7.1 确定状态表示
我们一般是以某一个位置为结尾,或者是以某一个位置为开始来确定状态表示;
结合经验以及题目要求:
我们想尝试一下,以某一个位置结尾定义状态表示能否推出状态转移方程,如若不能推出,则就以某一个位置为开始来定义状态表示:
dp[i] 表示:在第 i 天结束的时候,所获得的利润最大值;而实际上在第 i 天结束的时候有两种状态:1、手中有股票 2、手中无股票 ;并且还要求了“最多只进行两笔交易”,再继续细分下去,其子状态是非常多的,但从整体上可以划分为两个状态:“买入”、“卖出”,并且还需要记录其交易次数(可以增加一维来记录交易次数)
此处我们两个状态使用两个dp表来解决,并且在两个dp 表的基础上再增加一个维度来记录交易次数;
- f[i][j]表示:在第 i 天结束之后,完成 j 次交易,此时处于“买入”状态下的,最大利润;
- g[i][j]表示:在第 i 天结束之后,完成 j 次交易,此时处于 “卖出”状态下的最大利润;
7.2 状态转移方程
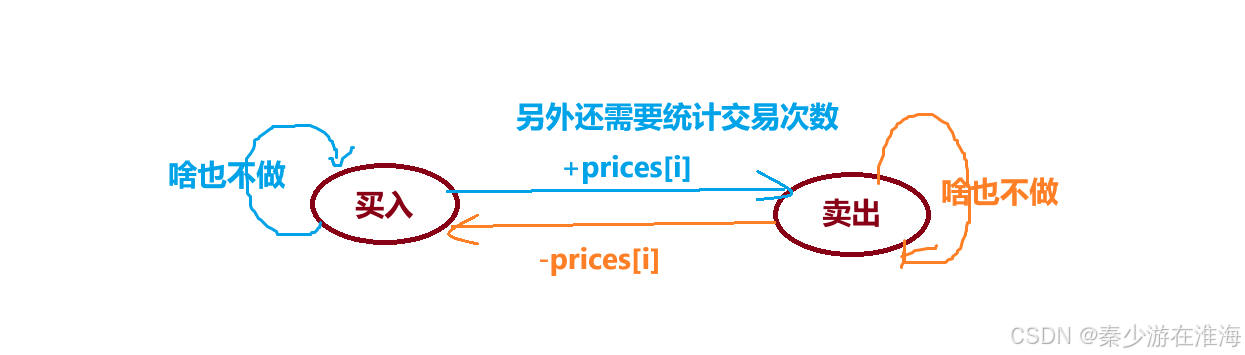
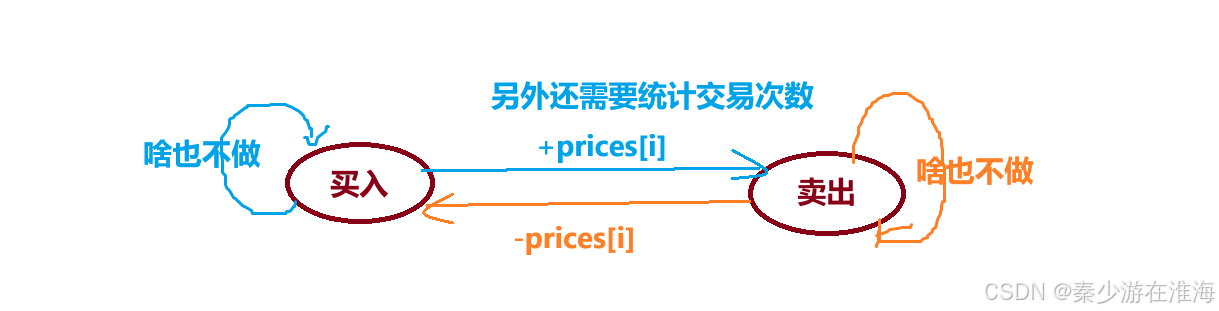
我们在卖出的时候统计交易次数;
从上图中可以分析得到:
买入:
- 第 i-1 天结束时为买入,在第 i 天啥也不做,那么第 i 天结束的时候仍为买入状态;
- 第 i-1 天结束时为卖出状态,在第 i 天买入,那么第 i 天结束的时候就为买入状态;
求这两种情况的最大值即可;
同理,也是这样对“卖出”情况进行分析;
状态转移方程:
f[i][j] = max(f[i-1][j] , g[i-1][j] - prices[i]);
g[i][j] = max(g[i-1][j] , f[i-1][j-1] + prices[i]);
需要注意的是 : f[i-1][j] 表示第 i-1 天结束,交易j次的最大利润; f[i-1][j-1] 表示第 i-1 天结束,交易 j-1 次的最大利润; g[i-1][j] :表示第 i-1 天结束,交易 j 次的最大利润;
f[i][j] 要求的是第 i 天结束时为”买入“的最大利润,可以是第 i-1天结束为“买入”,但第 i 天啥也不做;也可以是第 i-1 天为“卖出”,但第 i 天买入股票,取这两种情况的最大值即可;因为我们在“卖出“的时候统计交易次数,这两种情况均不涉及”卖出“,所以次数均为j;故而:f[i][j] = max(f[i-1][j] , g[i-1][j] - prices[i]);
g[i][j] 求的是第 i 天结束为”卖出“时最大利润;可以是第 i-1 天为”卖出“,但是第 i 天啥也不做;也可以是第 i-1 天为买入,但在第 i 天将该股票卖出,那么交易次数从 j-1 变成了 j;故而 g[i][j] = max(g[i-1][j] , f[i-1][j-1] + prices[i]);
7.3 初始化
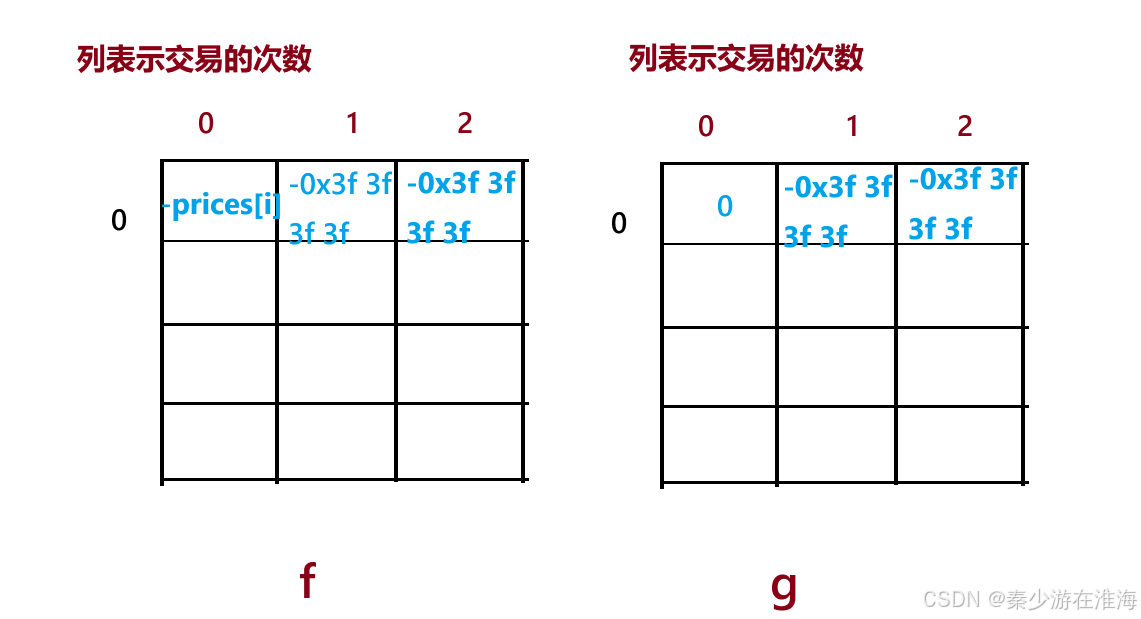
观察我们的状态转移方程,当 i 为0 的时候,下标就不合法了;我们需要初始这 f表的第一行,g表的第一行;
当 j 为0的时候, j-1 才会越界,而 f[i-1][j-1] 中的 j-1 表示的是在第 i-1 天结束的时候,完成了一笔 -1笔交易,显然就是不存在的状态;在填表的时候判断一下就好;
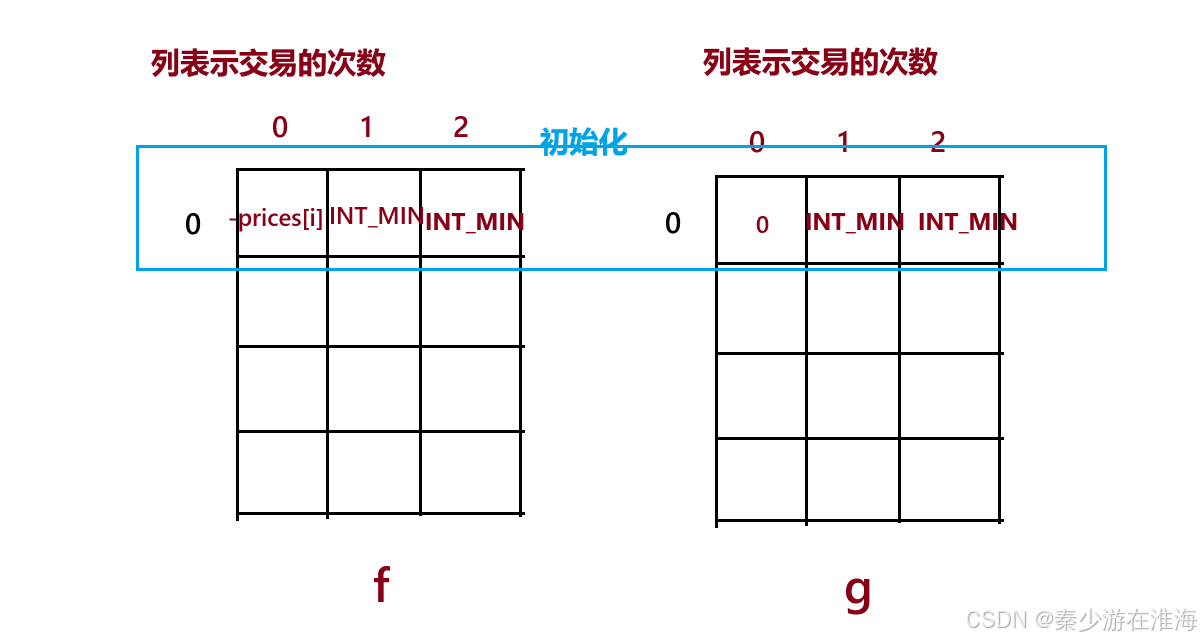
第0天,完成一笔交易、两笔交易一定是不存在的;因为如果在1天中如果买入又卖出,就会白白浪费一次交易,且利润为0;本题中的交易次数是有限的;所以 f[0][1] = INT_MIN , f[0][2] = INT_MIN; g[0][1] = INT_MIN , g[0][2] = INT_MIN;
f[0][0] 表示第0天结束为”买入“,交易0次的最大利润 --> f[0][0] = -prices[0];
g[0][0] 表示第 0 天结束为”卖出“,交易0次的最大利润 --> g[0][0] = 0;
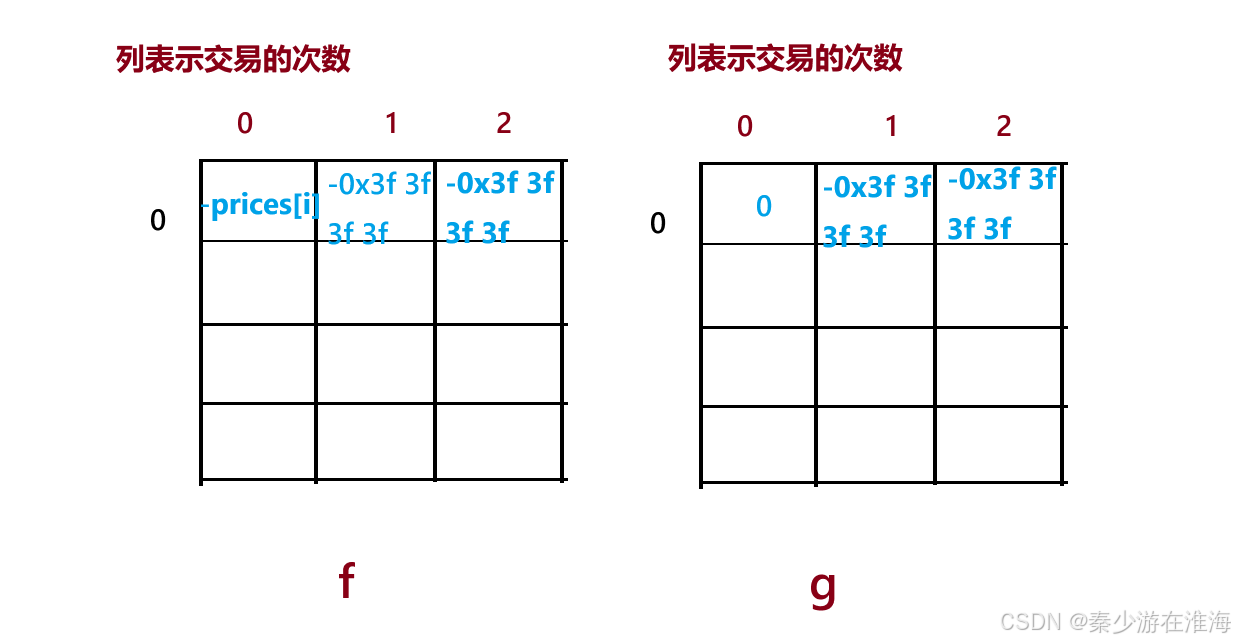
细节问题:在选择最大的负数的时候,不适使用INT_MIN,而是使用INT_MIN的一半: -0x3f 3f 3f 3f ;
如果初始化为INT_MIN,那么 f[i][j] = max(f[i-1][j] , g[i-1][j] - prices[i]); 那么 INT_MIN - prices[i] 就会超过int 可以存放数据的最小范围,此时编译器可能会报错或者转换成正数;而使用 -0x 3f 3f 3f 3f 就可以规避这个问题;
使用 -0x3f 3f 3f 3f 的好处:1、此数足够小,小到本题的最终结果均不会小于此数,即使用该数不会影响最终的结果;2、在 -0x3f 3f 3f 3f 上做加、减操作的时候,不会超过int 类型可表示的数据的范围;
7.4 填表顺序
两个dp 表是相互影响的,所以在填表的时候两个表需要一起填写;
从上往下填写每一行,每一行从左往右进行填写,两个表一起填;
7.5 返回值
题干要求:![]() ;而最后一天结束时为”买入“状态一定不是最大的利润,所以最大利润在 g 表中;而交易次数可以是0次、1次、2次,所以返回值为 g 表最后一行中的最大值;
;而最后一天结束时为”买入“状态一定不是最大的利润,所以最大利润在 g 表中;而交易次数可以是0次、1次、2次,所以返回值为 g 表最后一行中的最大值;
参考代码:
int maxProfit(vector<int>& prices)
{
int n = prices.size();
vector<vector<int>> f(n,vector<int>(3,-0X3f3f3f3f));
auto g = f;
//初始化
f[0][0] = -prices[0] , g[0][0] = 0;
//填表
for(int i = 1;i<n;i++)
{
for(int j = 0;j<3;j++)
{
//两个表同时填写
f[i][j] = max(f[i-1][j] , g[i-1][j]-prices[i]);
g[i][j] = g[i-1][j];
if(j>=1) g[i][j] = max(g[i][j] , f[i-1][j-1]+prices[i]);
}
}
return max(g[n-1][0] , max(g[n-1][1],g[n-1][2]));
}8、题8 买卖股票的最佳时机 IV :
188. 买卖股票的最佳时机 IV - 力扣(LeetCode)

梳理:不能同时参与多笔交易,最多交易 k 次,求最大利润;
需要注意的是,如果当天买当天卖是没有任何意义的;所以我们需要先处理一下细节 ; k = min(k , n/2);
8.1 确定状态转移方程
状态表示一般是以某一个位置为开始,或者以某一个位置为结束;
结合经验以及题目要求:
我们想尝试一下,以某一个位置结尾定义状态表示能否推出状态转移方程,如若不能推出,则就以某一个位置为开始来定义状态表示:
dp[i] 表示:在第 i 天结束的时候,所获得的利润最大值;而实际上在第 i 天结束的时候有两种状态:1、手中有股票 2、手中无股票 ;并且还要求了“最多只进行 k 笔交易”,再继续细分下去,其子状态是非常多的,但从整体上可以划分为两个状态:“买入”、“卖出”,并且还需要记录其交易次数(可以增加一维来记录交易次数)
此处我们两个状态使用两个dp表来解决,并且在两个dp 表的基础上再增加一个维度来记录交易次数;
- f[i][j]表示:在第 i 天结束之后,完成 j 次交易,此时处于“买入”状态下的,最大利润;
- g[i][j]表示:在第 i 天结束之后,完成 j 次交易,此时处于 “卖出”状态下的最大利润;
8.2 状态转移方程
本题与上一题很像,无非就是交易次数不同;我们还是在卖出的时候统计交易次数;
f[i][j] = max(f[i-1][j] , g[i-1][j] - prices[i]);
g[i][j] = max(g[i-1][j], f[i-1][j-1] + prices[i]);
8.3 初始化
同理:
8.4 填表顺序
从上往下填写每一行,每一行从左往右,两个表同时填写;
8.5 返回值
返回 g 表中最后一行中的最大值;
参考代码:
int maxProfit(int k, vector<int>& prices)
{
int n = prices.size();
//处理细节
k = min (k , n/2);
vector<vector<int>> f(n,vector<int>(k+1,-0x3f3f3f3f));
auto g = f;
//初始化
f[0][0] = -prices[0], g[0][0] = 0;
//填表
for(int i = 1;i<n;i++)
{
for(int j = 0;j<=k;j++)
{
//两个表同时填写
f[i][j] = max(f[i-1][j] , g[i-1][j] - prices[i]);
g[i][j] = g[i-1][j];
if(j>=1) g[i][j] = max(g[i][j] , f[i-1][j-1] + prices[i]);
}
}
int ret = 0;
for(int j = 0;j<=k;j++)
{
ret = max(ret, g[n-1][j]);
}
return ret;
}总结
动态规划五个步骤:
- 1、确定一个动态表达式
- 2、根据该动态表达式来推导状态转移方程
- 3、初始化
- 4、填表顺序
- 5、返回值
一般有三种方式可以来确定状态表示:
1、题目怎么要求,我们就怎么定义状态表示
2、经验 + 题目要求
3、分析题目的过程中发现重复的子问题(再将重复的子问题抽象为状态表达式)
推导状态转移方程:1、用之前或者之后的状态推导得到dp[i] 的值 ; 2、根据最近的一步来划分问题;
初始化的目的:保证填dp表(根据状态转移方程来调表)的时候不会发生越界;
填表顺序的目的是为了保证在填表的时候,所要依据的状态已经存在了;






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








