二叉树的先序遍历 递归与迭代

1.题目

二叉树的先序遍历

2.数据结构与算法

递归：
迭代：引入辅助栈，处理递归嵌套问题。

3.源代码

模板类定义，参考我的文章：《二叉树BT 模板类实现》
这里只给出实现各版本先序遍历的代码。

//沿左侧链遍历辅助函数
template<typename T1> 
template<typename T, typename VST> 
static void BinNode<T1>::visitAlongLeftBranch(stack<BinNodePosi(T)> &s, BinNodePosi(T) x, VST &visit){
	while(x){
		visit(x);
		if(HasRChild(x)) s.push(x->rChild);
		x = x->lChild;
	}
}

//递归
template<typename T1> 
template<typename T, typename VST> 
void  BinNode<T1>::travPre_R(BinNodePosi(T) x, VST &visit){
	if(!x) return;
	visit(x->data);
	travPre_R(x->lChild, visit);
	travPre_R(x->rChild, visit);
}

//迭代1
template<typename T1> 
template<typename T, typename VST> 
void  BinNode<T1>::travPre_I1(BinNodePosi(T) x, VST &visit){
	stack<BinNodePosi(T)> s; //辅助栈
	if(x) s.push(x); //根节点入栈
	while(!s.empty()){
		x = s.top();s.pop();visit(x); 
		if(HasLChild(*x)) s.push(x->rChild); //右孩子先入栈
		if(HasRChild(*x)) s.push(x->lChild); //左孩子后入栈
	}
}

//迭代2
template<typename T1> 
template<typename T, typename VST> 
void  BinNode<T1>::travPre_I2(BinNodePosi(T) x, VST &visit){
	if(!x) return;
	stack<BinNodePosi(T)> s;
	while(true){
		visitAlongLeftBranch(s, x, visit);
		if(s.empty()) break;
		x = s.top(); s.pop();
		
	}
}

4.时间复杂度

时间复杂度都是$o(n)$，但是其系数是大有不同的。
递归：每个递归实例有通用的格式，并不能做到足够的小。
迭代1：引入辅助栈处理递归嵌套问题，使每一帧保存的数据足够小。
迭代2：先序遍历有着沿左侧链访问的特点，进而进一步优化，减少入栈出栈次数。

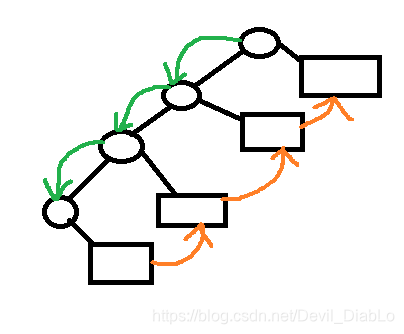
5.结论

最优先序遍历：迭代2

如有错误，请您批评指正。
参考书籍：清华大学《数据结构（C++语言版）》（第三版） 邓俊辉