LCS 递归与DP迭代

1.题目

给定两个字符串，两个字符串的公共子串中最长的即为"最长公共子串" LCS

2.数据结构与算法

给定两个字符A[0, n), B[0, m)

递归实现：比较两个字符串的末尾字符，总共有3种情况

1.递归基：m=0或 n=0,

其中一个字符为空字符，直接返回空串即可。

2. 末字符 A[n-1] == B[m-1] == "X"

减而治之: lcs(A[0, n-1), B[0,m-1)) + “X”
其中
子问题：两子串的lcs问题
平凡问题：子问题的解拼接“X”

3.末字符 A[n-1] ！= B[m-1]，

减而治之：取 lcs( A(0, n-2), B(0, m-1)) 与 lcs( A(0, n-1), B(0, m-2))中的更长者
其中
子问题：认为这两个末字符其中一个对LCS是没有贡献的，分别砍掉其中一个子串的末字符，求解LCS。
平凡问题：子问题得到的两个LCS中取较大者为解。

DP迭代实现
数据结构：二维数组、（字符输出采用stack）

思想：由自上而下的递归，转而自下而上的迭代。

构建LCS表:

步骤一.初始化下图二维数组c,图中蓝色线元素值为0

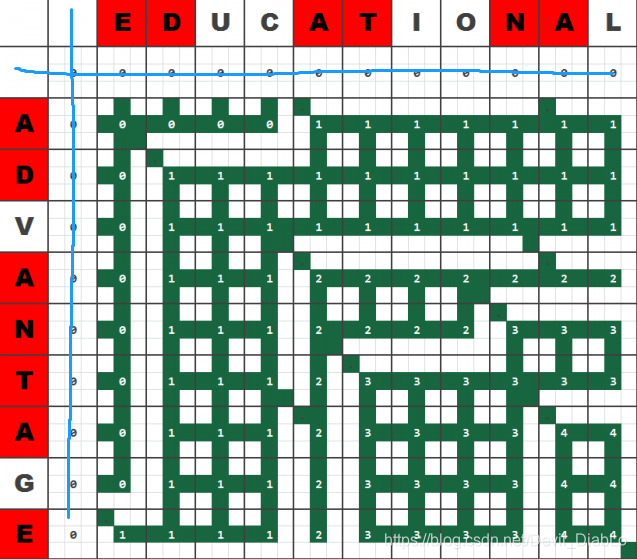
步骤二：从左至右，从上至下扫描
我们再引入一个数组b，用于记录回溯方向。（1代表左上，2代表上，3代表左）

情况1：:扫描到两字符相等

令c[i][j] = c[i-1][j-1] + 1; //等于左上角值+1
令b[i][j] = 1;记录此处方向为左上

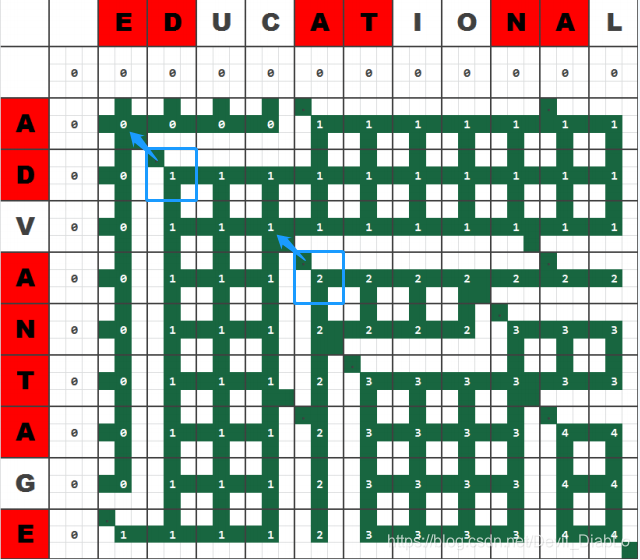
情况2：扫描到两个字符不相等

令c[i][j] = (c[i-1][j] >c[i][j-1]) ? c[i-1][j] : c[i][j+1]; //c[i][j]取左边或上边最大者
令b[i][j] = (c[i-1][j] >c[i][j-1]) ? 3 : 2; //b[i][j] 记录向着更大者的方向，若向左和向上相等，我们先自定义让他向上。

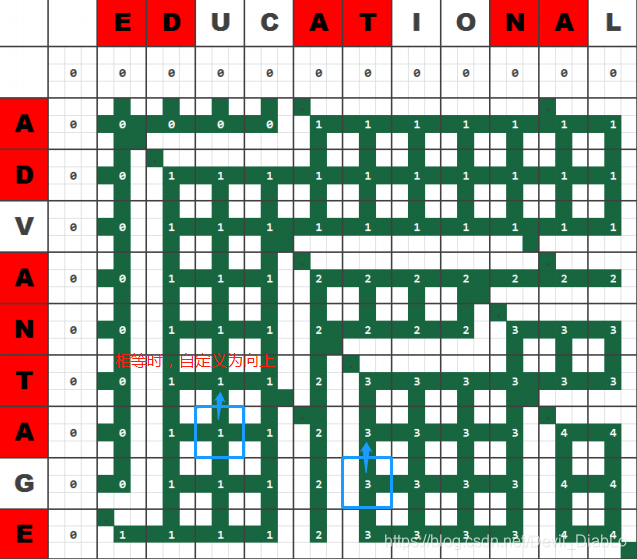
回溯：
只需根据刚刚的b表所指示的方向进行回溯就能得到一个LCS。

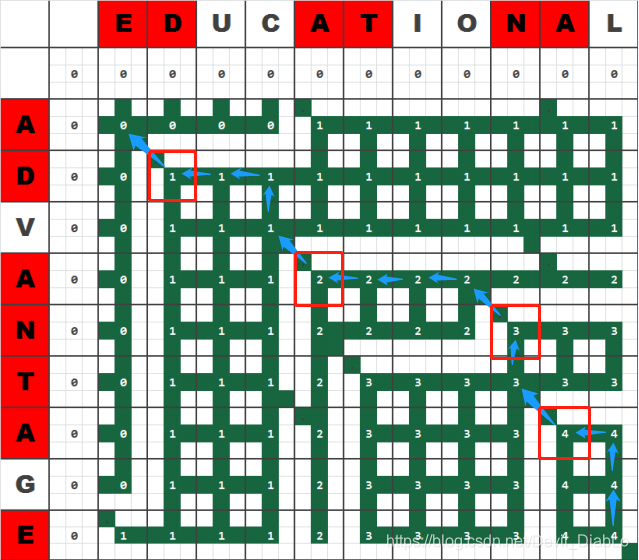
3.源代码

#include "stdafx.h"
#include <iostream>
#include <string>
#include <stack>
using namespace std;

//最长公共子序列长度

//递归实现,返回lcs中的一个
string lcs(string a, string b){

	int n = a.size(); 
	int m = b.size();

	if(n == 0 || m ==0)
		return "";

	if(a[n-1] == b[m-1]){
		return lcs(a.substr(0, n-1), b.substr(0, m-1)) + a[n-1];
	}else{
		string str1 = lcs(a.substr(0, n-1), b.substr(0, m));
		string str2 = lcs(a.substr(0, n), b.substr(0, m-1));
		return (str1.size()>str2.size()) ? str1 : str2; //此处改为>=得到另一个结果 "dana"
	}
}

//DP迭代实现:返回lcs中的一个，和
 void lcs2(string str1, string str2){

	//构造lcs表
	int m = str1.size() + 1;
	int n = str2.size() + 1;

	int **c = new int* [m];
	int **b = new int* [m]; //同时构造表b, 便于代码书写

	for(int i=0; i<m; i++){
		c[i] = new int[n];
		b[i] = new int[n];
	}
	for(int i=0; i<m; i++){
		c[i][0] = 0;
		b[i][0] = 0;
	}
	for(int i=0; i<n; i++){
		c[0][i] = 0;
		b[0][i] = 0;
	}
	
	for(int i=0; i<m-1; i++){
		for(int j=0; j<n-1; j++){
			if(str1[i] == str2[j]){
				c[i+1][j+1] = c[i][j] + 1;
				b[i+1][j+1] = 1; //使用数字1代表左上方向
			}else{
				if(c[i+1][j] >= c[i][j+1]){  //此处若修改为>，得到另一个lcs："dana"
					c[i+1][j+1] = c[i+1][j];
					b[i+1][j+1] = 2; //使用数字2代表上方向
				}else{
					c[i+1][j+1] = c[i][j+1];
					b[i+1][j+1] = 3; //使用数字3代表左方向
				}
			}
		}
	}

	//输出数组c
	for(int i=0; i<m; i++){
		for(int j=0;j<n; j++){
			cout<<c[i][j]<<" ";
		}
		cout<<endl;
	}

	stack<char> lcs; //使用栈保存字符

	int i = m-1, j = n-1;
	while(c[i][j] != 0){
		if(b[i][j] == 1){
			lcs.push(str1[i-1]);
			i--;
			j--;
		}else{
			(b[i][j] == 2)? j-- : i--;
		}
	}

	//输出lcs
	cout<<"其中一个lcs：";
	while(!lcs.empty()){
		cout<<lcs.top();
		lcs.pop();
	}


	//释放内存
	for(int i=0; i<m; i++){
		delete [] c[i];
		delete [] b[i];
	}

	delete []c;
	delete []b;
}


int main()
{
	string str1 = "advantage";
	string str2 = "educational";

	//递归
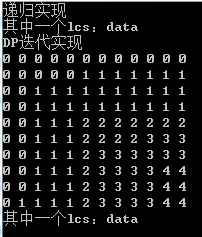
	cout<<"递归实现\n其中一个lcs："<<lcs(str1, str2)<<endl;

	//DP迭代
	cout<<"DP迭代实现"<<endl;
	lcs2(str1, str2);

	//防止窗口关闭
	cin.get();
}

输入：

输出

4.时间复杂度

递归实现：
最好的情况：总是出现第二种情况（两字符相等），只需要$o(m+n)$的时间
在最坏的情况下：总是不出现第二种情况（即两字符相等）。
使用组合数分析：需要比较从(0, 0)到(m, n)所有路径中的最长者的所有可能情况。
C(m+n, m) = C(m+n, n)
若m = n; 则需要$o(2^n)$的时间

迭代实现：
显然需要$o(m\ast n)$的时间，即其时间主要耗费在构造LCS表。
空间复杂度也为$o(m\ast n)$

5.结论

递归方式编写代码虽然清晰、简单。但算法性能往往并不如迭代算法。

究其原因，递归算法往往产生大量重复的递归实例。

如有错误，请您批评指正。
参考书籍：清华大学《数据结构（C++语言版）》（第三版） 邓俊辉