PTA(B)1003我要通过

PTA(B)1003我要通过

题面

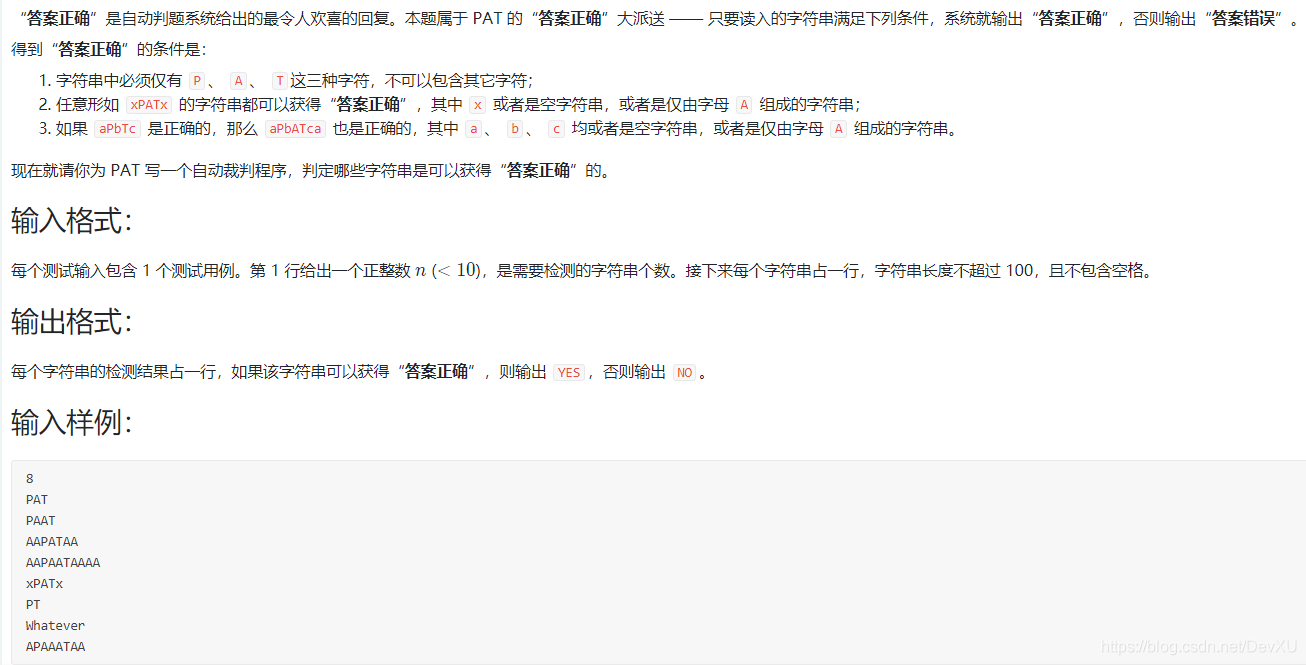
这个题目其实通过举例子可以找到规律:
注意XPATX中的X代表字符串，只要左右两边完全相同就可以认为符合。比如:
AAPATAA
APATA
PAT
…
紧接着题面说如果aPbTc符合,那么aPbATca符合
观察一下aPbTc---->aPbATca变化了什么?
不难发现当b多增加一个A，右边的c多增加了整个a字符串，而且数量也是1!而且结合第一个条件知道P和T左右两边永远只能是A。
那么有如下推导式:

P左边的A个数*P和T中间的A个数 = T右边的A个数

附加条件:

字符串里只能含有P、A、T，且P、T仅一个，T必须在P的右边至少第二个位置。

代码如下:

#include <iostream>
#include <string>
using namespace std;
int main()
{
    int n;
    string s;
    cin >> n;
    for(int i = 0;i < n;i++){
        cin >> s;
        int r;
        for(r = 0;r < s.size();r++){
            if(s[r] != 'P' && s[r] != 'A' && s[r] !='T')
                break;
        }
        if(r != s.size()) { cout << "NO" << endl; continue; }
        int p;
        for(p = 0;p < s.size() && s[p] != 'P';p++);
        if(p == s.size()) { cout << "NO" << endl; continue; }
        int t;
        for(t = 0;t < s.size() && s[t] != 'T';t++);
        if(t == s.size()) { cout << "NO" << endl; continue; }
        if(t < p || p+1 == t) { cout << "NO" << endl; continue; }
        int la = 0,ma = 0,ra = 0;
        int j;
        for(j = 0;j < s.size();j++){
            if(s[j] != 'A' && j != p  && j != t) { cout << "NO" << endl; break; }
            if(j < p) la++;
            if(j > p && j < t) ma++;
            if(j > t) ra++;
        }
        if(j == s.size()){
            if(la*ma == ra) cout << "YES" << endl;
            else cout << "NO" << endl;
        }
    }
    
    return 0;
}

时间复杂度O(n*max(s.size()))，而n<10，max(s.size())<=100，故完全可行。