一、主成分分析
1.简述
主成分分析是一种统计方法,通过正交变换将一组可能存在相关性的变量转换成一组线性不相关的变量,转换后的这组变量叫主成分。
PCA的思想是将n维特征映射到m维上(m<n),这m维是全新的正交特征,称为主成分,这m维的特征是重新构造出来的,不是简单的从n维特征中减去n-m维特征。PCA的核心思想就是将数据沿最大方向投影,数据更易于区分。
主成分矩阵(n * p)由原数据矩阵(n * p)点乘特征向量矩阵(p * p)得来(n为数据的个数,p为数据的属性个数),表示特征向量将原数据沿特征值最大(即方差最大)的方向投影,得到主成分。特征值是主成分贡献率的体现,一个主成分的特征值越大,该主成分的贡献率就越大。

2.代码
clear
clc
%传入数据集
% openExample("spectra.mat")
load spectra.mat
%调用主成分分析函数
%四个返回值分别是特征向量、主成分、特征值、特征值所占百分比
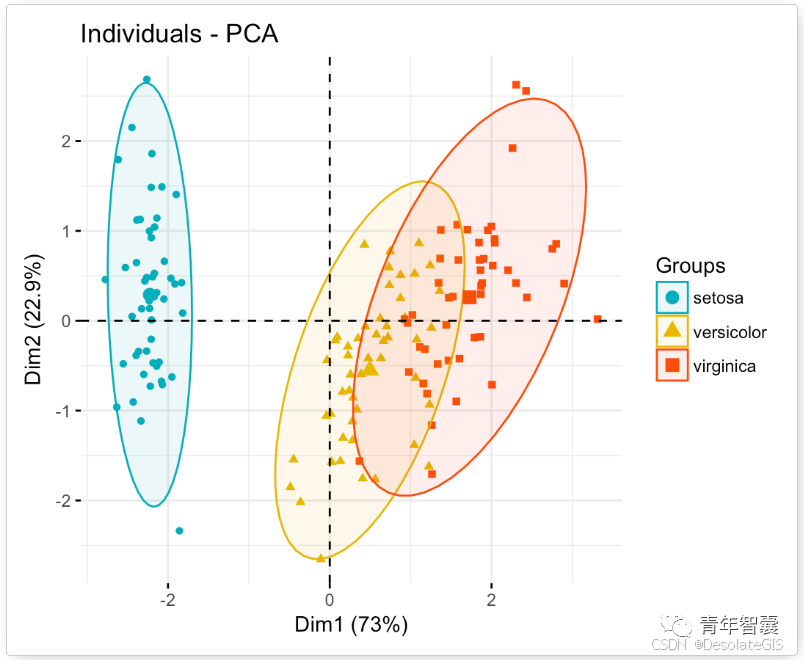
[PCA_Vector, PCA_Score, PCA_Var, ~, explained, ~] = pca(NIR);
%绘图
pareto(explained);
xlabel('主成分');
ylabel('贡献率(%)');
title('主成分贡献率');
3.运行结果
二、偏最小二乘回归
1.简述
偏最小二乘法(Partial Least Squares, PLS)是一种统计学和机器学习中的多元数据分析方法,特别适用于处理因变量和自变量之间存在多重共线性问题的情况。PLS通过寻找新的正交投影方向,使得投影后的因变量和自变量之间具有最大的协方差,从而建立预测模型。
PLS算法的核心思想是通过提取主成分来进行降维,同时最大化因变量和自变量之间的相关性。具体步骤如下:
-
提取主成分:计算自变量和因变量的协方差矩阵,通过迭代算法(如NIPALS算法)提取出第一组主成分,这组主成分既能反映自变量的变化趋势,又能反映因变量的变化趋势。
-
回归建模:将提取出的主成分作为新的自变量,对因变量进行线性回归建模。
-
重复迭代:对剩余的自变量残差继续提取新的主成分,并进行回归,直到满足预定的停止准则(如累计解释变异率达到设定阈值,或提取的主成分数目达到预设值)。
2.代码
clear
clc
%传入数据集
openExample("spectra.mat")
load spectra.mat
%随机划分训练集和测试集
index = randperm(60);
train_X = NIR(index(1 : 50), :);
train_Y = octane(index(1 : 50), :);
test_X = NIR(index(51 : end), :);
test_Y = octane(index(51 : end), :);
%k表示主成分的个数
k = 2;
%调用偏最小二乘回归函数
%返回值分别为自变量和因变量的特征向量、主成分,回归系数,特征值所占比例
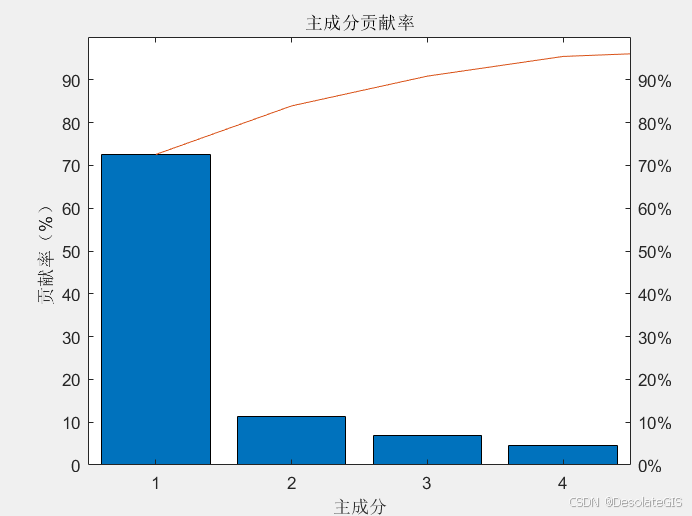
[PLS_X_Vector, PLS_Y_Vector, PLS_X_Score, PLS_Y_Score, BETA, explained, ~, ~] = plsregress(train_X, train_Y, k);
%绘图
pareto(explained(:, 1));
xlabel('主成分');
ylabel('贡献率(%)');
title('主成分贡献率');
%测试数据
sim_Y = [ones(10, 1) test_X] * BETA;
%计算相对误差
error = (test_Y - sim_Y) / test_Y;
figure(2);
%绘图
plot_x = 1 : 10;
plot(plot_x, test_Y, 'r-', plot_x, test_Y, 'ro');
hold on
plot(plot_x, sim_Y, 'b-.', plot_x, sim_Y, 'b*');
3.运行结果
 MATLAB降维:PCA与PLS方法解析
MATLAB降维:PCA与PLS方法解析





















 693
693

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








