浅谈模拟退火

模拟退火

简介

模拟退火是一种随机化算法。
对于一个当前最优解附近的非最优解，爬山算法直接舍去了这个解。而很多情况下，我们需要去接受这个非最优解从而跳出这个局部最优解，即为模拟退火算法。
当一个问题的方案数量极大（甚至是无穷的）而且不是一个单峰函数时，常使用模拟退火求解。

实现

如果新状态的解更优则修改答案，否则以一定概率接受新状态。

模拟退火时有三个参数：初始温度T_0，降温系数d ，终止温度T_k。

是一个比较大的数（至少需要大于搜索范围，）是一个非常接近但是小于的数是一个接近的正数定义当前温度为，新状态与已知状态（由已知状态通过随机的方式得到）之间的能量差为，（当要求的为最大值时）发生状态转移（修改最优解）的概率为当新解优于最优解时，

否则P(Delta E)=e^{frac{Delta E}{T}}

首先让温度T=T_{0}，进行转移尝试，再让T=T*d。当T<T_k时模拟退火过程结束，当前最优解即为最终的最优解。
有时为了使得到的解更有质量，会在模拟退火结束后，以当前温度在得到的解附近多次随机状态，尝试得到更优的解（其过程与模拟退火相似）。

随着温度的降低，跳跃越来越不随机，最优解也越来越稳定

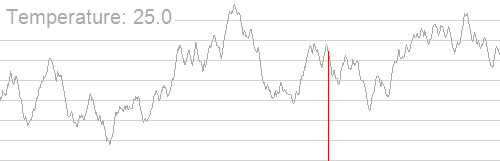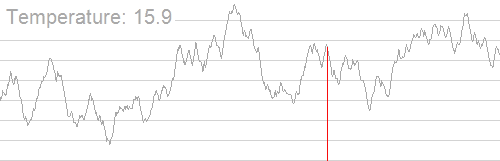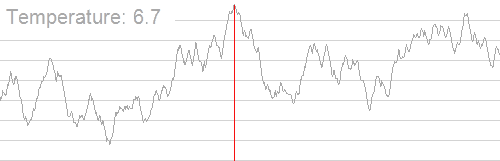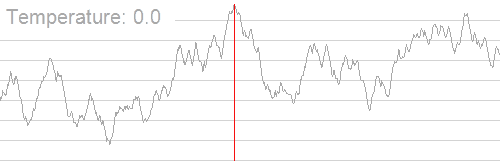
例题

1.JSOI2004平衡点/吊打XXX

当重力势能最小时稳定，将物理模型简化
设桌子的高度为h，绳子的长度为l,每个点到x的距离为dis[i]
重力势能为sum_{i=1}^{n}(h-(l-dis[i]))*W[i]

由于h-l为定值，所以重力势能最小的情况等价于sum_{i=1}^{n}dis[i]*W[i]最小
即 求n个点的带权费马点