从CoT到O1推理模型，简单聊聊LLM的Test-Time Scale Law

概述：

自2022年11月OpenAI发布ChatGPT以来，大语言模型(LLM)在推理能力方面展现出了惊人的潜力。然而，早期的大模型在处理复杂推理任务时仍然存在明显的局限性：推理过程不透明、结果缺乏可靠性、难以处理多步骤的复杂问题等。这些挑战促使研究人员开始探索更高效的推理方法。Chain of Thought推理方法的出现源于一个重要观察：当人类解决复杂问题时，往往需要经过清晰的思维步骤。研究者发现，通过提示模型"一步步思考"（step-by-step thinking），可以显著提升模型在数学问题、逻辑推理等任务上的表现。2024年9月，OpenAI推出了专门针对推理能力优化的O1模型，这是一个通过强化学习训练的新型大语言模型，专门用于执行复杂推理任务。一经发布，就在各个领域中展现出了远超GPT4o等传统大模型的推理能力，几个月后今天，国内的几家大模型企业，如gemini、Qwen、deepseek、kimi等，也陆续推出了各自的推理模型产品或开源模型。本文中，我们将围绕大模型test-time的策略，介绍CoT和推理模型部分技术原理和方案，欢迎各位朋友批评和交流。

COT

Chain of Thought是一种提示技术（prompting technique），通过引导大语言模型展示其推理过程的中间步骤，从而提高其在复杂任务中的表现。

什么是CoT

这种方法最早由Google Research团队在2022年提出，通过论文 "Chain-of-Thought Prompting Elicits Reasoning in Large Language Models" 【1】正式引入学术界。本节内相关内容同时参考了【2】。

CoT的基本形式

以下表述，我们快速了解CoT和一般prompt的主要区别，以及CoT的基本形式。 标准的大模型输出，可以直接输出答案，简洁，但是在处理较复杂问题时会影响其准确率：

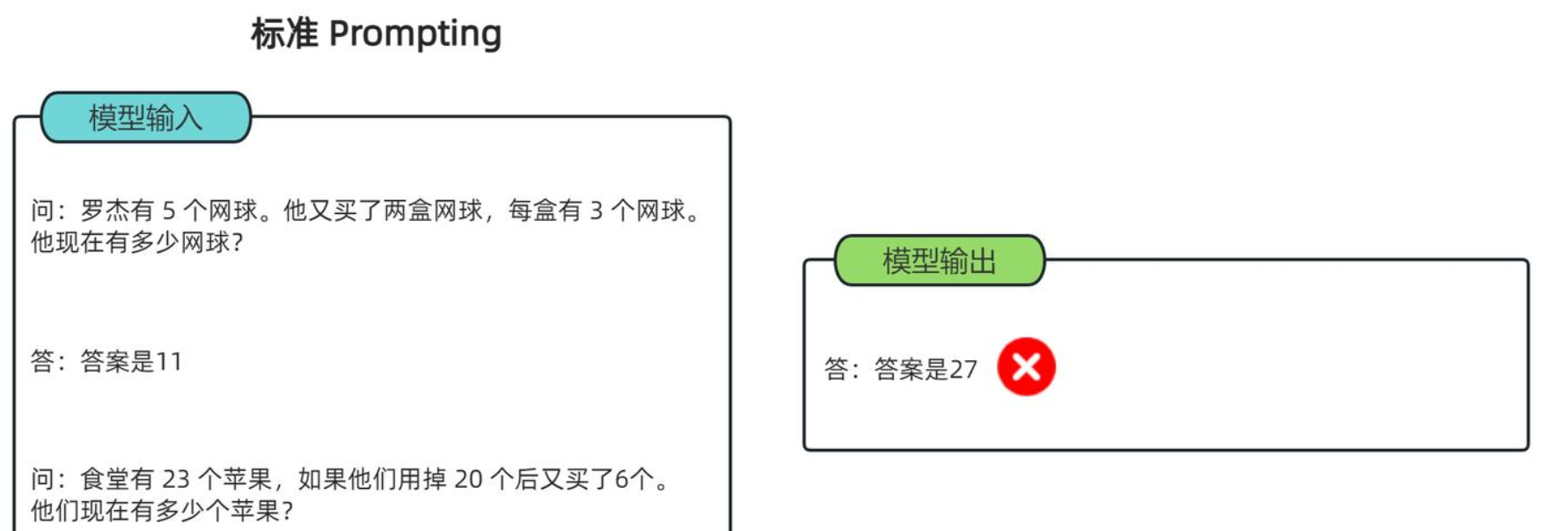
Few-shot CoT模式下，提示中带有推理步骤的示例，通过示例引导模型学习推理模式，适用于复杂任务和特定领域问题：

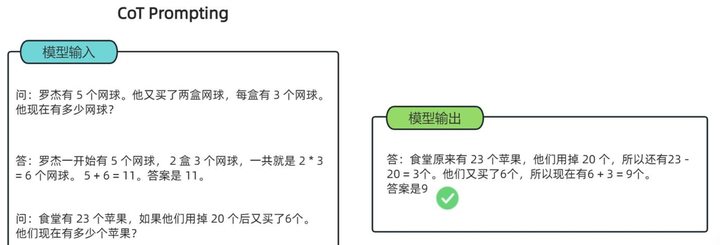
Zero-shot CoT，通过在提示中加入特定关键词，如“Let's think step by step”，无需示例即可激活模型的推理能力，适用于相对简单的推理任务：

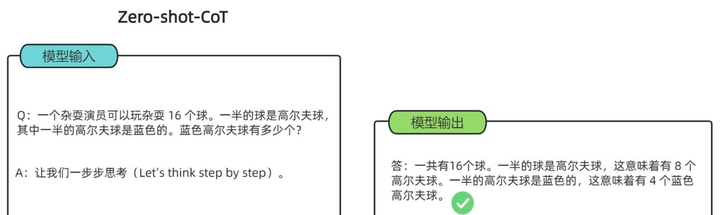
在【2】中，作者研究了通过什么样的prompt，可以得到最优的zero-shot-CoT效果，感觉比较有趣：

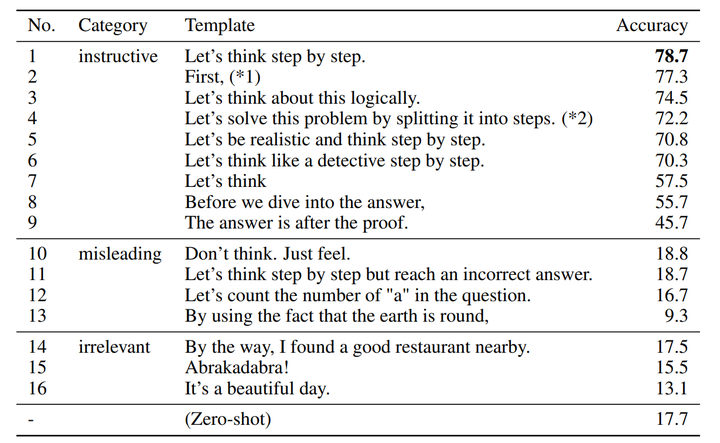
可以看到，在MultiArith数学数据集上，合适的CoT推理，可以比起传统的prompt，取得更加正确的结果。

Self-consistency

Self-consistency CoT，即通过多个推理路径得到答案，然后通过多数表决或一致性检查选择最可靠的答案，从而提高推理结果的可靠性。

本部分我们主要参考论文【3】，下图为论文【3】中示例，说明了基本的self-consistency和一般CoT的主要区别。

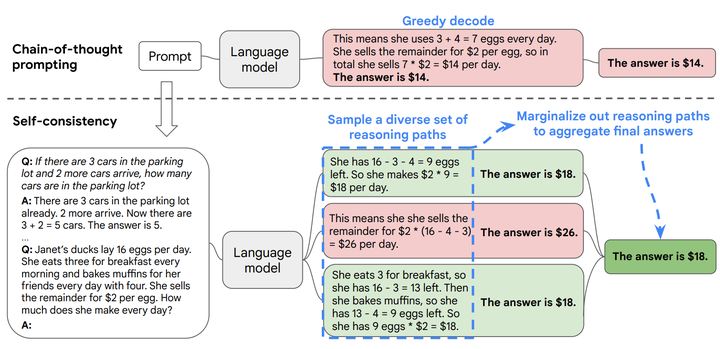
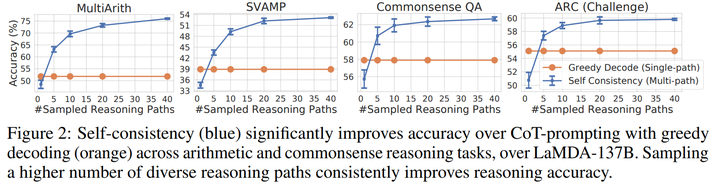
以下结果来自于【3】，表明self-consistency的数量会影响最终的效果。

least to most prompting（LtM）

Least-to-Most Prompting 是一种新型的提示技术，最初由Google Research团队提出。这种方法的核心思想是将复杂问题分解成一系列更简单的子问题，然后逐步解决，最终达到解决复杂问题的目的。该章节主要参考论文【4】。

下图说明了LtM的基本过程，首先基于大模型的能力对复杂问题进行拆分，然后依次回答独立的子问题，最后总结给出最后的答案。

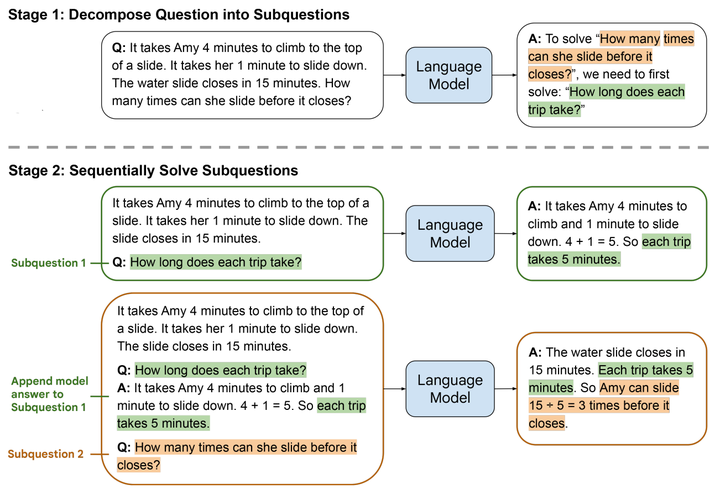
LtM的主要优势为，能够提高复杂问题的推理能力，具有更好的可控性。

下图为【4】中的实验结果，在code-davinci-001、code-davinci-002、text-davinci-001等数据集上，LtM均取得了显著的提升。

COT的发展方向

在了解了基本的CoT的形式和功能之后，我们参考上海交大的一篇综述性论文【5】，来总结CoT模式转变的几个方向。

a)Prompt 模式

指令生成模式

1.手动指令生成

通过手动添加prompt，使得大模型进行CoT推理，如Zero-Shot-CoT使用的“Let's think step by step”，或者Plan-and-Solve（PS）【6】使用的“Let’s first understand the problem and devise a plan to sol