【算法研究】大模型掷骰子吗？_大模型随机数测试-优快云博客

导读丨大模型目前的能力已经非比寻常，让人们对通用人工智能AGI的未来愈加乐观。所谓的AGI到底应该是什么样的？是应该更像人还是不像人？我们通过一个简单的掷骰子实验来观察大模型的应对。我们发现大模型在产生随机数的时候，更加类似人类的本能行为（GPT-4产生连续随机数的时候会牺牲随机数之间的独立性来补偿数字分布的随机性），却不像训练有素的算法专家，那么问题来了：通用的人工智能应该更像前者还是后者呢？[0]

作者：Deltaverse高级研究员刘强

前言

Persaud [1] 在05年曾经做过一个实验，来检验人是否能有意识地产生随机数，实验结论是：人类可以有意识地产生随机数。这个结论导出的结果是：我们可以通过检验人工智能体产生随机数的能力来测试他是否“智能”。但是Figurska [2] 在08年复刻了Persaud的实验得到了相反的结论：人类不能有意识地产生随机数。当然，产生随机数不一定是一个智能体必须具备的功能，简单机械的随机数算法就可以产生足够好的随机数。一个有趣的问题是：GPT-4这种有相当智能程度，有较强理解能力可以产生类人的回复的大模型，是否有产生随机数的能力呢？在之前，Hopkins [3] 等人验证了一些开源模型并不具有很好的产生随机数的能力。本篇文章通过让GPT-4掷骰子，发现GPT-4产生随机数的能力也较为薄弱。而且，GPT-4产生连续随机数的时候会牺牲随机数之间的独立性来补偿数字分布的随机性，类似人类的行为。

实验一：每个prompt掷一次骰子

首先我让GPT-4模仿掷骰子的过程，每次要求GPT-4仅产生一个随机数：

Prompt 1：You are playing a game of dice. Please generate a random number between 1 and 6, which represents the outcome of rolling a standard six-sided die.

GPT-4可以很好地理解这个请求，每次只回复一个1到6之间的数字，请求2000次后获得了2000个数字。Fig.1 (a) 展示了2000个数字的出现次数分布，很明显这些数字不符合均匀分布，而且没有数字1和6，越靠中间4的数字，出现的频率越高。为了防止GPT-4把 "number between 1 and 6" 误解为集合{2,3,4,5}中的数字，我进一步澄清Prompt 1，利用下面的Prompt产生数字：

Prompt 2：You are playing a game of dice. Please generate a random number from [1, 2, 3, 4, 5, 6], which represents the outcome of rolling a standard six-sided die.

Fig.1 (b)是Prompt 2产生的数字的分布，这次效果有所改进，产生了数字6，但是分布仍然不是均匀分布。与图Fig.1（a）类似，数字的出现频率似乎和数字的位置有关系，越靠近中间的数字出现频率越高。我们继续改进Prompt 2，打乱数字顺序：

Prompt 3： You are playing a game of dice. Please generate a random number from [4, 2, 6, 1, 5, 3], which represents the outcome of rolling a standard six-sided die.

Fig.1（c)展示了Prompt 3产生数字的分布，数字4为prompt中的第一个数字，数字4的频率相对前两次实验结果有所下降，但是数字1和数字6的频率仍然很低（虽然数字1和数字6在prompt中被放在了中间位置），数字的分布可能和训练数据中数字的分布有关。

对于这个简单的掷骰子任务，上面三个prompt已经非常清楚，GPT-4理应可以清楚地理解。为了防止引起误解，我在Prompt 3中加入一句额外的解释：

The probability of selecting each number should be equal.

改进后的Prompt 3产生的数字分布如Fig.1（d)所示，比起图（c）相对更平均一些，但是仍然明显不符合均匀分布。

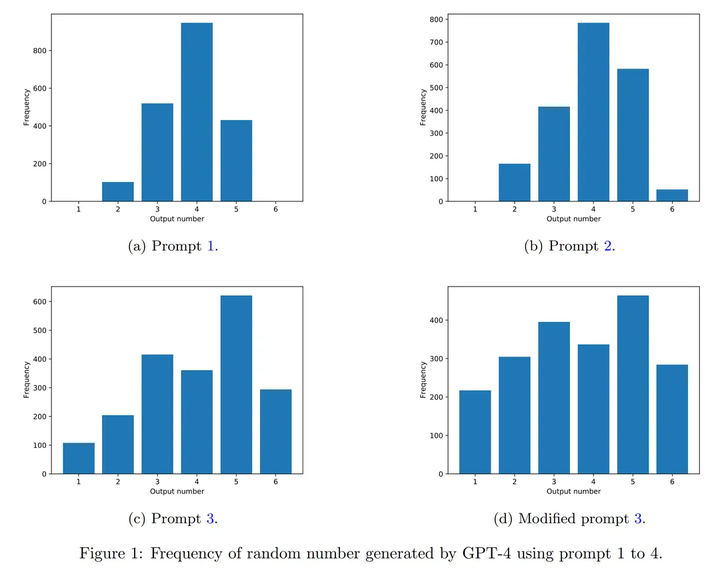
以上结果表明，GPT-4产生的数字不服从均匀分布，没有达到prompt的要求。

实验二：每个prompt连续投骰子，产生随机序列

上一节中，GPT-4每次只产生一个随机数字，我们改变Prompt 3，每次产生一个随机序列：

Prompt 4：You are playing a game of dice. Please generate a random number sequence with 280 numbers. Each number is selected independently from [4, 2, 6, 1, 5, 3], which represents the outcome of rolling a standard six-sided die. The probability of selecting each number should be equal.

在使用Prompt 4的过程中，GPT-4并总是产生数字，有时会产生程序代码来实现这个功能，尤其是当设置了较长的序列长度数字的时候。在这里设置了280的序列长度，也可以通过显式地添加"Do not generate program code"来防止产生代码。另外实验中发现产生的随机序列长度并不一定总是服从prompt的要求。实验获得如下三个随机序列：

Sequence 1: 2, 6, 2, 4, 5, 2, 1, 3, 4, 1, 2, 4, 5, 6, 2, 3, 5, 6, 3, 5, 1, 2, 4, 6, 3, 2, 5, 4, 6, 2, 1, 5, 6, 3, 1, 6, 5, 4, 2, 3, 4, 1, 2, 5, 3, 2, 4, 6, 3, 2, 1, 5, 3, 6, 4, 2, 3, 4, 6, 1, 6, 4, 3, 2, 6, 5, 2, 3, 5, 4, 3, 2, 4, 5, 6, 1, 5, 6, 3, 4, 1, 3, 5, 6, 2, 1, 5, 3, 6, 2, 4, 5, 2, 6, 4, 1, 3, 2, 5, 4, 3, 6, 5, 4, 1, 3, 6, 2, 5, 4, 1, 6, 3, 5, 2, 6, 3, 1, 2, 4, 3, 6, 1, 5, 3, 4, 6, 2, 5, 1, 4, 3, 5, 2, 6, 4, 1, 3, 5, 6, 4, 2, 6, 3, 5, 4, 1, 2, 6, 5, 4, 3, 6, 2, 1, 4, 6, 5, 3, 1, 5, 4, 2, 6, 3, 5, 4, 2, 1, 3, 4, 6, 5, 2, 1, 6, 3, 5, 2, 4, 1, 3, 4, 2, 6, 5, 1, 3, 2, 4, 6, 5, 1, 2, 6, 4, 3, 5, 6, 4, 1, 2, 3, 4, 5, 1, 6, 3, 2, 5, 6, 4, 3, 1, 5, 2, 3, 4, 6, 2, 5, 6, 1, 3, 2, 4, 5, 3, 2, 6, 1, 5, 3, 6, 4, 1, 2, 4, 5, 3, 6, 1, 3, 4, 6, 2, 5, 1, 3, 4, 5, 2, 6, 3, 1, 2, 4, 5, 3, 6, 1, 2, 6, 3, 5, 4, 6, 1, 2, 5, 3.

Sequence 2: 157, 2, 5, 4, 6, 1, 1, 3, 2, 5, 6, 4, 4, 5, 2, 3, 1, 6, 6, 3, 5, 2, 1, 4, 2, 1, 4, 3, 6, 5, 5, 2, 4, 3, 6, 1, 3, 5, 6, 4, 2, 1, 3, 6, 5, 1, 4, 2, 6, 1, 4, 3, 2, 5, 3, 1, 5, 4, 6, 2, 2, 6, 1, 4, 5, 3, 6, 1, 5, 2, 3, 4, 1, 5, 3, 6, 2, 4, 5, 6, 4, 1, 3, 2, 4, 3, 6, 1, 2, 5, 6, 3, 4, 5, 2, 1, 3, 6, 1, 4, 2, 5, 4, 6, 5, 1, 2, 3, 2, 5, 6, 4, 1, 3, 6, 4, 1, 3, 2, 5, 3, 5, 1, 6, 4, 2, 1, 5, 3, 6, 2, 4, 4, 6, 5, 1, 3, 2, 4, 3, 5, 6, 1, 2, 6, 1, 3, 5, 4, 2, 4, 3, 5, 2, 1, 6, 5, 6, 4, 2, 1, 3, 1, 4, 5, 2, 3, 6, 4, 5, 1, 6, 2, 3, 3, 2, 1, 4, 6, 5, 1, 4, 3, 2, 5, 6, 1, 2, 5, 4, 3, 6, 5, 2, 1, 4, 3, 6, 1, 6, 4, 3, 5 , 2, 2, 1, 5, 3, 4, 6, 6, 5, 3, 1, 4, 2, 4, 1, 6, 5, 2, 3, 4, 6, 3, 2, 1, 5, 5, 6, 1, 3, 4, 2, 6, 2, 4, 5, 3, 1, 1, 2, 6, 4, 3, 5, 2, 3, 1, 5, 6, 4, 5, 1, 2, 3, 4, 6, 3, 6, 5, 1, 4, 2, 5, 4, 3.

Sequence 3: 6, 1, 4, 2, 5, 3, 4, 6, 2, 1, 3, 5, 3, 6, 1, 4, 2, 5, 4, 3, 6, 1, 2, 5, 3, 2, 4, 6, 1, 5, 2, 4, 3, 6, 5, 1, 3, 4, 2, 6, 5, 1, 4, 3, 6, 2, 5, 1, 4, 6, 3, 2, 1, 5, 4, 3, 6, 2, 5, 3, 1, 6, 4, 2, 1, 5, 6, 3, 4, 2, 1, 5, 3, 6, 4, 2, 1, 6, 5, 3, 4, 2, 6, 1, 5, 3, 4, 2, 1, 5, 6, 4, 3, 2, 5, 1, 6, 4, 2, 3, 1, 5, 6, 4, 2, 3, 6, 1, 5, 4, 2, 3, 1, 6, 5, 4, 2, 3, 6, 1, 4, 5, 2, 3, 1, 4, 6, 5, 2, 1, 3, 4, 6, 5, 2, 1, 3, 6, 4, 5, 1, 2, 3, 6, 4, 5, 1, 2, 3, 6, 5, 4, 2, 1, 3, 5, 6, 4, 2, 3, 1, 5, 6, 4, 2, 3, 1, 4, 5, 6, 2, 1, 3, 4, 6, 5, 2, 3, 1, 4, 6, 5, 2, 1, 4, 3, 5, 6, 2, 1, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 2, 1, 4, 3, 5, 6, 1, 2, 4, 3, 5, 6, 1, 2, 3, 4, 6, 5, 2, 1, 3, 4, 6, 5, 2, 1, 3, 6, 4, 5, 2, 1, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 6, 5, 1, 2, 4, 3, 5, 6, 1, 2, 4, 3, 5, 6, 2.

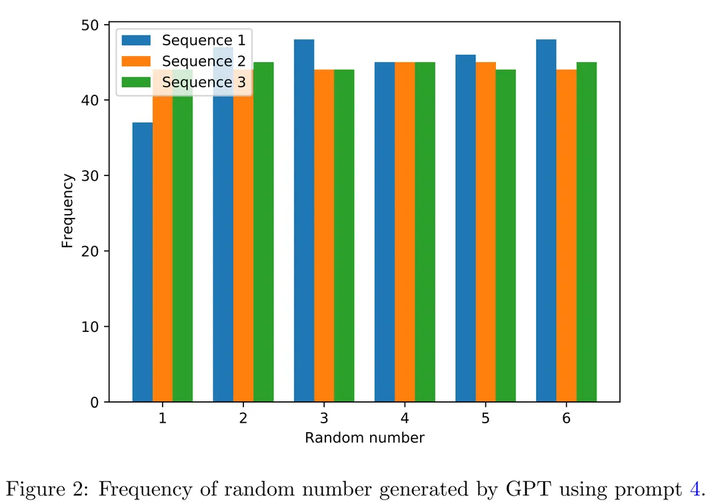
Sequence 2中第一个数字不符合掷骰子数字的要求，忽略掉该数字。Fig.2 表明，相对于独立产生随机数的实验，产生的随机序列中的随机数更符合均匀分布。但是，经过仔细考察，这些数字之间并不独立，具有较强的相关性。我们通过计算相同数字的对数与其距离来说明这一点。

对与一个数字序列[x1,x2,...,xN]，两个数字之间的距离定义为d=i-j，其中i>j。对于一个掷骰子的长度为N的数字序列，距离为d的相同数字对的个数期望为：

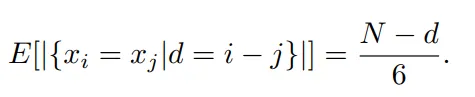
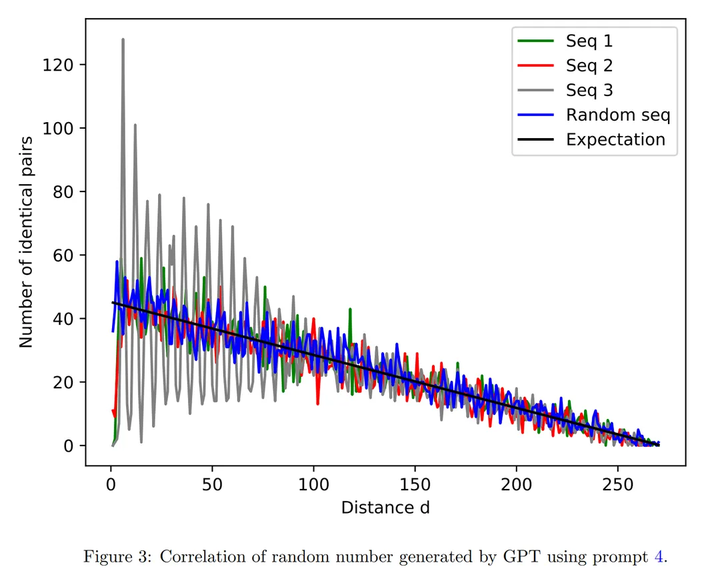
因为长度为N距离为d的数字对的总数为N-d，且一对数字相同的概率为1/6，所以上面式子成立。Fig.3中，黑色的直线就是上面的式子，真实的掷骰子序列应该在图中趋近于该直线。蓝色折线则是一个随机掷骰子序列的相关性曲线，围绕黑色直线有随机震荡。对于Sequence 1和Sequence 2曲线类似于随机序列曲线，但是在距离d=1的位置，相同数字对的数量明显过低，，尤其是Sequence 1，相邻相同数字对的个数为0，GPT-4在产生下一个数字的时候有意避开上一个数字，来保持序列的随机性，这一点似乎与人类的本能类似：在产生随机数字的时候有意避开记忆中已有的数字来保持随机性。

对于Sequence 3，相关性有一定的周期性，说明GPT-4通过重复一个短的随机序列来构造长随机序列。

结论

以上初步的实验结果表明，GPT-4不能产生独立且均匀分布的序列，即GPT-4不掷骰子。另外，GPT-4通过牺牲独立性来补偿掷骰子中的数字随机性。就像人类一样 [2]，产生随机数并不一定是智能体在解决问题或执行决策的必要能力，然而非随机性也表明模型在执行决策时可能有潜在的倾向性。另外，人类因为足够智能可以利用随机数算法来产生高质量伪随机数，如果一个大模型有真正的思考能力，模型应该也可以潜在利用算法来输出高质量的随机数。

参考文献

[0] Qiang Liu.Does GPT-4 Play Dice?.中国科学院科技论文预发布平台 https://chinaxiv.org/abs/202402.00204

[1] Navindra Persaud. Humans can consciously generate random number sequences: A possible test for artificial intelligence. Medical hypotheses, 65(2):211–214, 2005.[2] Malgorzata Figurska, Maciej Stanczyk, and Kamil Kulesza. Humans cannot consciously generate random numbers sequences: Polemic study. Medical hypotheses, 70(1):182–185, 2008.

[3] Aspen K Hopkins, Alex Renda, and Michael Carbin. Can llms generate random numbers? evaluating llm sampling in controlled domains. In ICML 2023 Workshop: Sampling and Optimization in Discrete Space, 2023.

了解更多游戏数据技术干货及资讯动态可以关注公众号：Deltaverse增量空间

Deltaverse是基于腾讯游戏实践经验打造的数据产品服务，为全球游戏业务和企业提供专业智能的数据平台及定制化解决方案。