P4219 [BJOI2014]大融合

博客园食用更佳：https://www.cnblogs.com/sonnety-v0cali0d-kksk/p/17470300.html

题目链接

题目描述：

[BJOI2014]大融合
题目描述

小强要在 $N$ 个孤立的星球上建立起一套通信系统。这套通信系统就是连接 $N$ 个点的一个树。

这个树的边是一条一条添加上去的。

在某个时刻，一条边的负载就是它所在的当前能够联通的树上路过它的简单路径的数量。

例如，在上图中，现在一共有了 $5$ 条边。其中，$(3,8)$ 这条边的负载是 $6$，因为有六条简单路径 $2-3-8$,$2-3-8-7$,$3-8,3-8-7$,$4-3-8$,$4-3-8-7$ 路过了 $(3,8)$。

现在，你的任务就是随着边的添加，动态的回答小强对于某些边的负载的询问。

输入格式

第一行包含两个整数 $N,Q$,表示星球的数量和操作的数量。星球从 $1$ 开始编号。

接下来的 $Q$ 行，每行是如下两种格式之一：

• A x y表示在 $x$ 和 $y$ 之间连一条边。保证之前 $x$ 和 $y$ 是不联通的。
• Q x y表示询问 $(x,y)$ 这条边上的负载。保证 $x$ 和 $y$ 之间有一条边。

输出格式

对每个查询操作，输出被查询的边的负载。

样例 #1

样例输入 #1

8 6
A 2 3
A 3 4
A 3 8
A 8 7
A 6 5
Q 3 8

样例输出 #1

6

提示

对于所有数据，$1\le N,Q\le 10^5$

---

~~私货：~~千百年后，智人在寰宇中销声匿迹，而Miku还在向沉默的星空唱出人性……孤立的星球尚且有人链接，而孤独的她只能孤独地发出自己的声音，人类的声音。

思路历程：

1.看样例图示，我认为是求边连接的两个点的出度相乘就是他们的负载。
过了样例，WA0暴力代码：

#include<bits/stdc++.h>
using namespace std;

const int maxn=1e4+50;

//思路：点出度*点出度等于边负载

int N,Q;
struct IN{
	char op;
	int x,y;
};IN in[maxn];

int d[maxn]; 
bool cont[maxn][maxn];
int head[maxn<<1],t;
struct edge{
	int u,v;
	int next_;
};edge e[maxn<<1];

void input(){
	scanf("%d%d",&N,&Q);
	char opt[2];
	int a,b;
	for(int i=1;i<=Q;++i){
		scanf("%s%d%d",&opt,&in[i].x,&in[i].y);
		in[i].op=opt[0];
	}
}

int main(){
	input();
	for(int i=1;i<=Q;++i){
		if(in[i].op=='A'){
			if(cont[in[i].x][in[i].y]==false){
				++d[in[i].x];
				++d[in[i].y];
				cont[in[i].x][in[i].y]==true;
				cont[in[i].y][in[i].x]==true;
			}
		}
		else{
			printf("%d\n",d[in[i].x]*d[in[i].y]);
		}
	}
	return 0;
}

2.我发现了输入数据1，并画出了图：

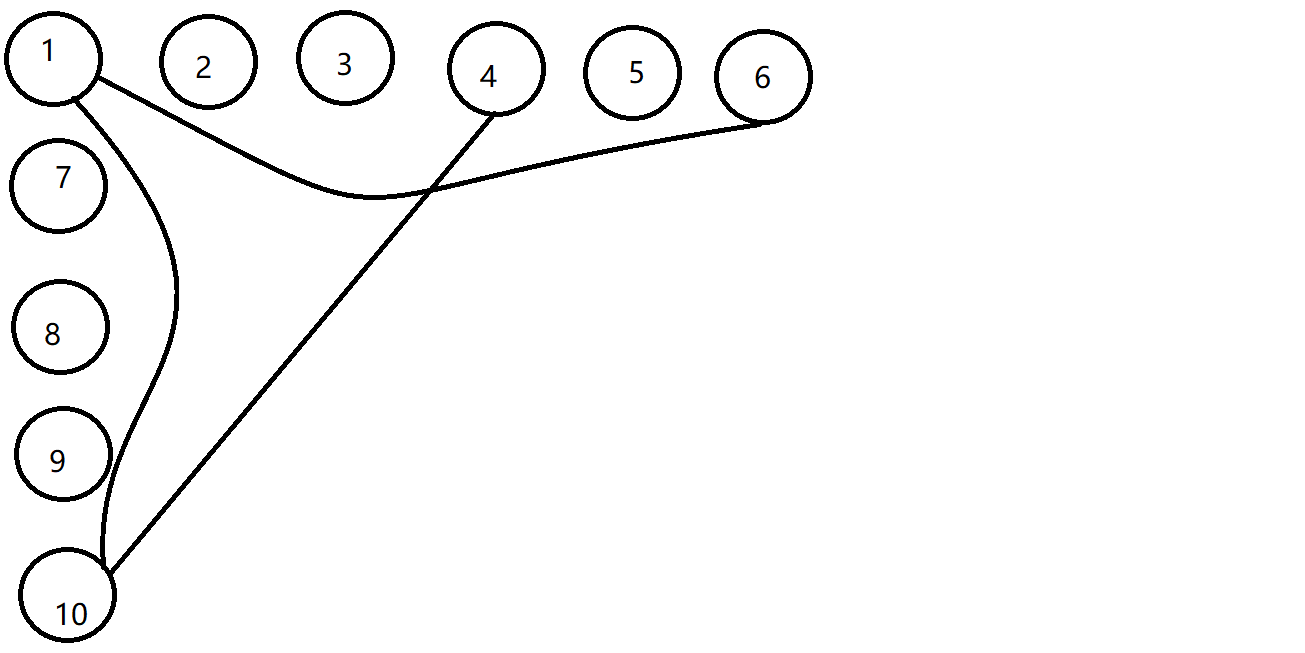
查4-10的边，有4-10-1-6,4-10-1,4-10三种，承载是3
但是4有一个出度，1有两个出度，乘积是2
我们重新审视一下这个样例：

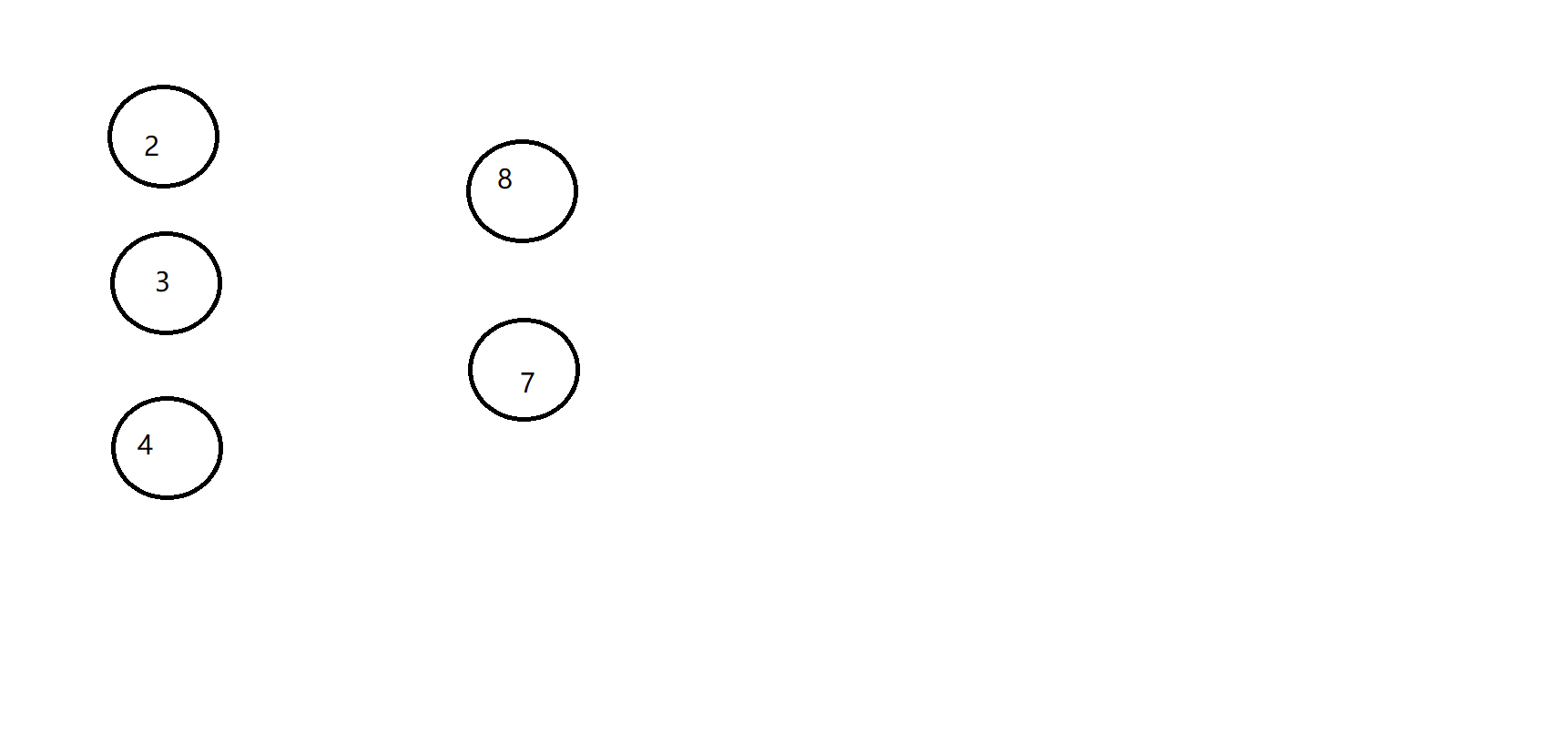
如果没有边，三个点连两个点，有几种方案数？
3*2==6
那么我们把边连起来：

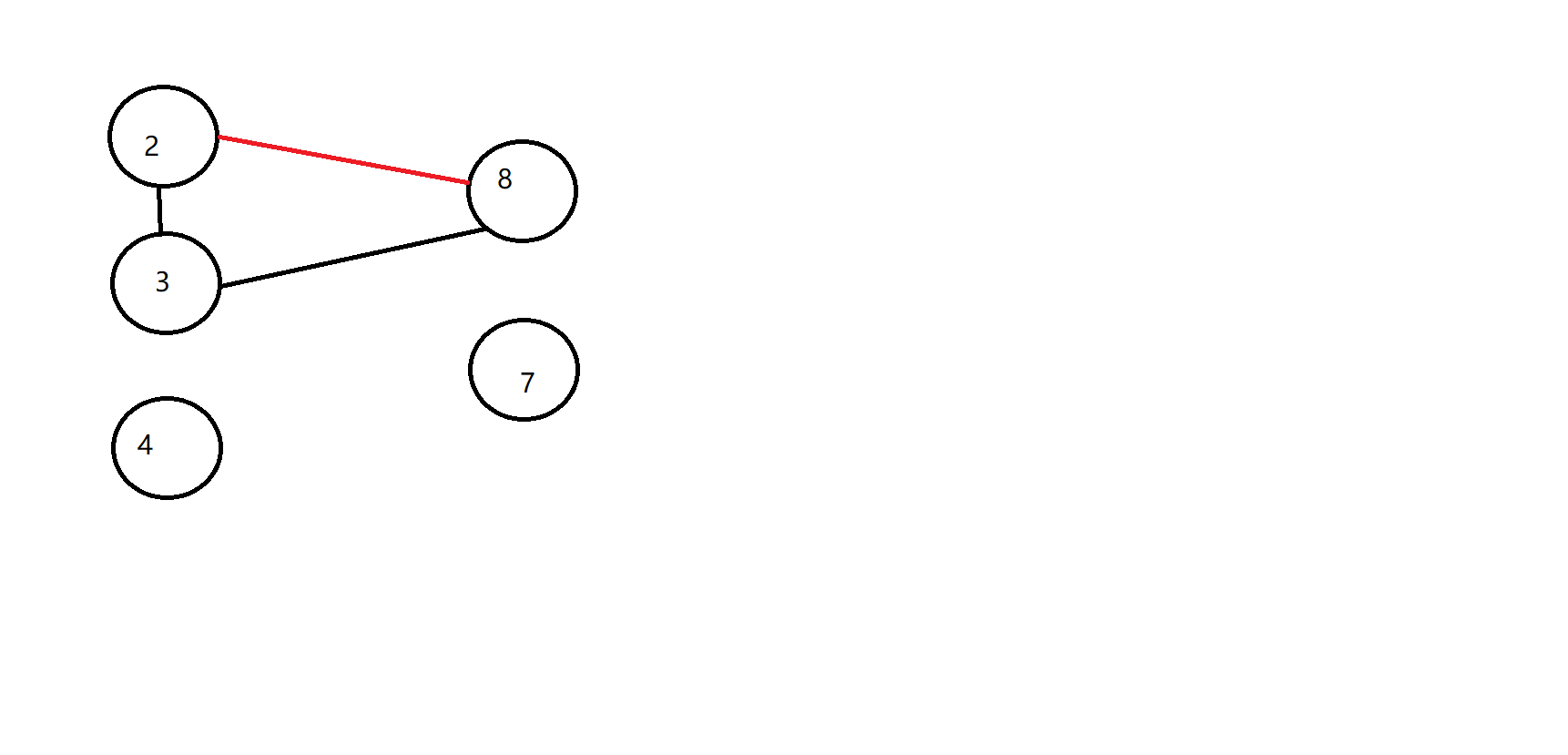
你看像不像向量（不是）
所以说，其实间接连和直接连是一样的…………
那么这个思路就很好构建了。
我们把给出的那条边“断开”，边上的点求一个集合，边下的点求一个集合，相乘。
那么如何实现呢？
都有上下一说了，那么我们构建dfs序，子节点直接查，父节点扔去子节点查。

---

完整代码：

Miku's Code

#include<bits/stdc++.h>
using namespace std;

const int maxn=1e5+50;
typedef long long intx;
#define ls tr[a].lid
#define rs tr[a].rid

int N,Q;
struct INPUT{
	char op;
	int x,y;
};INPUT iN[maxn];

int in[maxn],myf[maxn],sonum[maxn],tim; 

int head[maxn<<1],t;
struct edge{
	int u,v;
	int next_;
};edge e[maxn<<1];
void add_edge(int u,int v){
	e[++t].u=u;
	e[t].v=v;
	e[t].next_=head[u];
	head[u]=t;
}


int cnt;
struct TREE{
	int id,lid,rid;
	int sum;
};TREE tr[maxn<<5];

int fa[maxn];
int getfa(int x){
	if(x==fa[x])	return x;
	else return fa[x]=getfa(fa[x]); 
}

void input(){
	scanf("%d%d",&N,&Q);
	char opt[2];
	int a,b;
	for(int i=1;i<=Q;++i){
		scanf("%s%d%d",&opt,&iN[i].x,&iN[i].y);
		if(opt[0]=='A'){
			add_edge(iN[i].x,iN[i].y);
			add_edge(iN[i].y,iN[i].x); 
		}
		iN[i].op=opt[0];
	}
}

void dfs(int now,int fa){
	myf[now]=fa;
	sonum[now]=1;
	in[now]=++tim;
	for(int i=head[now];i;i=e[i].next_){
		int to=e[i].v;
		if(to==fa)	continue;
		dfs(to,now);
		sonum[now]+=sonum[to];
	}
}

void push_up(int a){
	tr[a].sum=tr[ls].sum+tr[rs].sum;
}

void update(int &a,int l,int r,int x){
	if(!a)	a=++cnt;
	if(l==r){
		tr[a].sum=1;
		return;
	}
	int mid=(l+r)>>1;
	if(x<=mid)	update(ls,l,mid,x);
	else 	update(rs,mid+1,r,x);
	push_up(a);
}

int merge(int a,int b,int l,int r){
	//cout<<"###"<<a<<' '<<b<<endl;
	if(!a||!b)	return a+b;
	if(l==r){
		tr[a].sum+=tr[b].sum;
		return a;
	}
	int mid=(l+r)>>1;
	ls=merge(ls,tr[b].lid,l,mid);
	rs=merge(rs,tr[b].rid,mid+1,r);
	push_up(a);
	return a;
}

intx query(int a,int l,int r,int x,int y){
	if(!a||y<l||x>r)	return 0;
	if(x<=l&&r<=y)	return tr[a].sum;
	int mid=(l+r)>>1;
	return query(ls,l,mid,x,y)+query(rs,mid+1,r,x,y);
}

int main(){
	input();
	for(int i=1;i<=N;++i){
		if(!in[i]){
			dfs(i,0);
		}
	}
	for(int i=1;i<=N;++i){
		update(tr[i].id,1,tim,in[i]);
		fa[i]=i;
	} 
	for(int i=1;i<=Q;++i){
		int fx=getfa(iN[i].x),fy=getfa(iN[i].y);
		if(iN[i].op=='A'){
			//cout<<"###"<<fx<<' '<<fy<<endl;
			fa[fy]=fx;
			tr[fx].id=merge(tr[fx].id,tr[fy].id,1,tim);
		}
		else{
			if(myf[iN[i].x]==iN[i].y)	swap(iN[i].x,iN[i].y);
			//cout<<iN[i].x<<' '<<tr[fy].id<<' '<<tim<<' '<<in[iN[i].x]<<' '<<in[iN[i].x]+sonum[iN[i].x]-1<<endl;
			intx ans1=query(tr[fx].id,1,tim,in[iN[i].y],in[iN[i].y]+sonum[iN[i].y]-1);
			intx ans2=query(tr[fx].id,1,tim,1,in[iN[i].y]-1)+query(tr[fx].id,1,tim,in[iN[i].y]+sonum[iN[i].y],N);
			//cout<<ans1<<' '<<ans2<<endl;
			intx ans=ans1*ans2;
			printf("%lld\n",ans);
		}
	}
	return 0;
}