二叉树遍历与操作全解析

一.

1. 二叉树的遍历

前序遍历：按照，根，左子树，右子数来遍历

中序遍历：按照，左子树，根，右子树来遍历

后续遍历：按照，左子树，右子树，根来遍历

层序遍历：一层一层往下

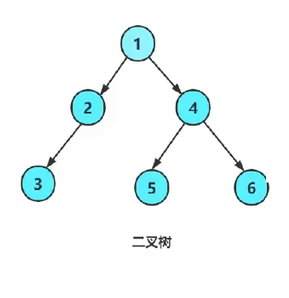
前序遍历：根为1，先左子树，为2，再左子树，为3，此时没有左子树了，也没右子树了，倒着往回推，2也没有右子树，1的右子树为4，再找左子树为5，5没左子树也没右子树，找4的右子树，为6；因此整体为 1 2 3 4 5 6；规律为，从根部一直找左子树，左子树为空再往回找右子树，找到根部接着再找右子树，再继续找左子树，为空往回找右子树。总结：往下遍历找左边，左边找完往上遍历找右边，找到根部再走右边，右边再往下遍历找左边，左边找完再往上遍历找右边。

中序遍历：先一直往左遍历，找到最左边的为3，3的根部为2，2没有右子树为空，再找根部为1，再在1的右子树里一直往左遍历，为5，5的根部为4，4的右子树为6。因此整体为3 2 1 5 4 6；总结：无论在哪个子树都先找最左边，再找根部，之后再找右边。

后续遍历：先找左子树的最左边为3，再找右子树为空，再找根部为2，2的右子树为空，根部为1，1的右子树的最左边为5，5是4的左子树，4的右子树为6，6的根部为4，4的根部为1，因此整体为3 2 5 6 4 1；总结：从根部开始，从左子树的叶子节点从左至右找，再上升一层继续从左往右，一直找到根部再在右子树重复以上步骤。

层序遍历：比较简单，一层一层从左往右再往下就行了，因此整体为1 2 4 3 5 6

前序的代码实现

//前序遍历
//根，左，右
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
		//返回到上一步
	}
	//根
	printf("%d ", root->data);
	//左
	//
	PrevOrder(root->left);
	//根的左子树全部找完才会进入右子树
	//右边
	PrevOrder(root->right);

}

中序的代码实现

//中序
//
//左，根，右
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
		//返回到上一步
	}
	//左
	InOrder(root->left);
	//根
	printf("%d ", root->data);
	//右
	InOrder(root->right);

}

后序的代码实现

//后序
//
//左，右，根
void LastOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
		//返回到上一步
	}
	//左
	LastOrder(root->left);
	//右
	LastOrder(root->right);
	//根
	printf("%d ", root->data);
}

结果如图

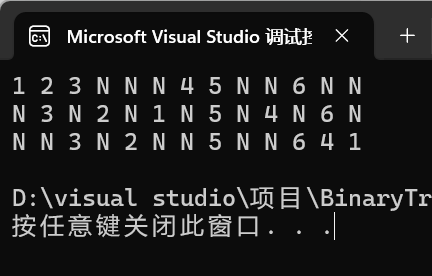
2 求二叉树节点的总个数

节点总个数个数=左子树+右子树+根（1），而且得注意不能访问空指针；

//节点总个数=左树个数+右树个数+1；
int TreeSize(BTNode* root)
{
	//如果为空树，直接返回0，
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

3 求叶子节点个数

如果节点的左子树和右子树都为空，说明此节点为叶子节点，记录下来，而且也不能访问空指针

//求叶子节点的个数
//首先得找到叶子节点，当左树和右树都为NULL时候为叶子节点，此时算找到一个叶子
//如果没有找到就继续向下找
//而且要先排除掉空树的情况，不能访问空指针
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

4 求二叉树的高度

高度=左子树和右子树里较高的树的高度+1

//求树的高度
//左树和右树里最高的一个+1；
int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	//重复计算过多，效率低下

	if (TreeHeight(root->left) >= TreeHeight(root->right))
		return TreeHeight(root->left) + 1;
	else
		return TreeHeight(root->right) + 1;

此代码满足上述要求，但是没有将已经计算过的高度记录下来，导致每次返回时需要再次计算，重复计算过多，导致效率低下，因此我们需要将已经计算过的高度记录下来，可以提高效率

//求树的高度
//左树和右树里最高的一个+1；
int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;

	int leftHeight = TreeHeight(root->left);

	int rightHeight = TreeHeight(root->right);

	if (leftHeight > rightHeight)
		return  leftHeight + 1;
	else
		return rightHeight + 1;

}

5 求第k层节点个数

（子问题）左子树的第k-1层节点个数 + 右子树第k-1层节点个数；当k等于1时，说明刚好是第k层的节点之一，返回一记录下来

//查找第k层数据节点个数
// 左子树的k-1层+右子树的k-1层
//k等于1就加1
int K_TreeSize(BTNode* root,int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return K_TreeSize(root->left, k - 1) + K_TreeSize(root->right, k - 1);
}

6.找出data为x的节点

易错点：return只能返回到上一层函数，因此我们需要将找到的节点保存下来，如果不为空，就一直return，直到完全返回

核心思想：先找左边，再找右边，保存下来，如果找到了（不为NULL）就层层返回（不能只返回一次），没找到就找右边，找到了也是层层返回，都没找到就返回NULL；

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	else if(root->data==x)
	{
		return root;
	}
//记录左边，找到x就层层返回
	BTNode* left= BinaryTreeFind(root->left, x);
	if (left != NULL)
	{
		return left;
	}
//记录右边
	BTNode* right = BinaryTreeFind(root->right, x);
	if (right != NULL)
	{
		return right;
	}
//都没有就返回NULL
	return NULL;
}

7 二叉树的创建

如果能给出一段字符串代表此二叉树的前中后序的任意一个，就可以更简便的将二叉树建立起来

用’#‘来代表空

BTNode* CreateTree(char* a, int* i)
{
	if (a[*i] == '#')
	{
		(*i)++;
		return NULL;
	}

	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	root->data = a[(*i)++];
	root->left = CreateTree(a, i);
	root->right = CreateTree(a, i);
	return root;
}