PyTorch实战线性回归

线性回归是机器学习的入门知识，应用十分广泛。
线性回归利用数理统计中的回归分析来确定两种或两种以上的变量间的相互依赖关系，其表述形式如下：
$$y=wx+b+e$$
误差e服从均值为0的正态分布。线性回归的损失函数是：

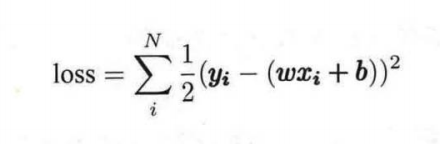
下面用PyTorch来实现一下线性回归，具体代码如下

import matplotlib.pyplot as plt
import torch
from torch import nn
from torch.autograd import Variable


x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
y = 2 * x + torch.rand(x.size())


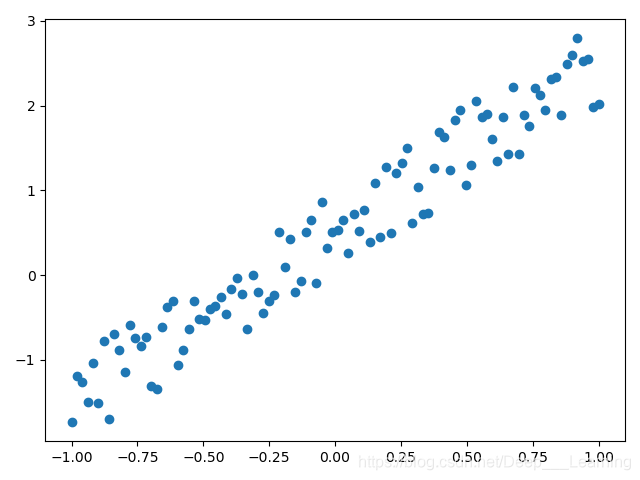
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = nn.Linear(1, 1)

    def forward(self, input_data):
        yy = self.fc(input_data)
        return yy


net = Net()
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
epochs = 10000
for epoch in range(epochs):
    inputs = Variable(x)
    target = Variable(y)

    output = net(inputs)
    loss = criterion(output, target)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if epoch % 100 == 0:
        print('Epoch: %d, loss: %.6f' % (epoch, loss.data.item()))

net.eval()
predict = net(Variable(x))
predict = predict.data.numpy()
plt.plot(x.numpy(), y.numpy(), 'ro', label='Original Data')
plt.plot(x.numpy(), predict, label='Fitting Line')
plt.show()

训练结果如下

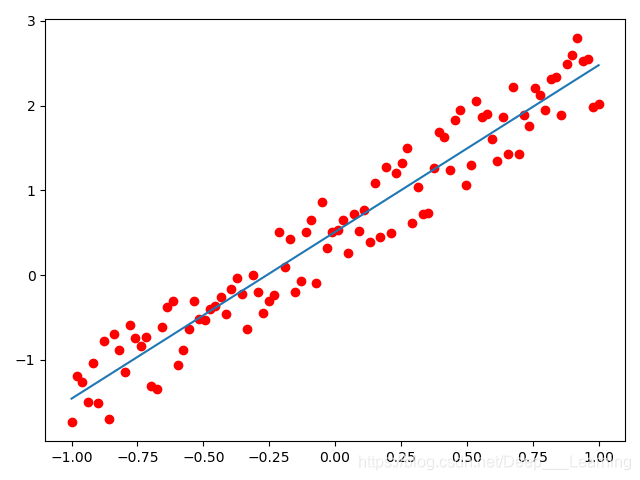
Epoch: 0, loss: 1.356474
Epoch: 100, loss: 0.308029
Epoch: 200, loss: 0.144987
Epoch: 300, loss: 0.105188
Epoch: 400, loss: 0.095055
Epoch: 500, loss: 0.092468
Epoch: 600, loss: 0.091807
Epoch: 700, loss: 0.091638
Epoch: 800, loss: 0.091595
Epoch: 900, loss: 0.091584
Epoch: 1000, loss: 0.091582
Epoch: 1100, loss: 0.091581
Epoch: 1200, loss: 0.091581
Epoch: 1300, loss: 0.091581
Epoch: 1400, loss: 0.091581
Epoch: 1500, loss: 0.091581
Epoch: 1600, loss: 0.091581
Epoch: 1700, loss: 0.091581
Epoch: 1800, loss: 0.091581
Epoch: 1900, loss: 0.091581
Epoch: 2000, loss: 0.091581
Epoch: 2100, loss: 0.091581
Epoch: 2200, loss: 0.091581
Epoch: 2300, loss: 0.091581
Epoch: 2400, loss: 0.091581
Epoch: 2500, loss: 0.091581
Epoch: 2600, loss: 0.091581
Epoch: 2700, loss: 0.091581
Epoch: 2800, loss: 0.091581
Epoch: 2900, loss: 0.091581
Epoch: 3000, loss: 0.091581
Epoch: 3100, loss: 0.091581
Epoch: 3200, loss: 0.091581
Epoch: 3300, loss: 0.091581
Epoch: 3400, loss: 0.091581
Epoch: 3500, loss: 0.091581
Epoch: 3600, loss: 0.091581
Epoch: 3700, loss: 0.091581
Epoch: 3800, loss: 0.091581
Epoch: 3900, loss: 0.091581
Epoch: 4000, loss: 0.091581
Epoch: 4100, loss: 0.091581
Epoch: 4200, loss: 0.091581
Epoch: 4300, loss: 0.091581
Epoch: 4400, loss: 0.091581
Epoch: 4500, loss: 0.091581
Epoch: 4600, loss: 0.091581
Epoch: 4700, loss: 0.091581
Epoch: 4800, loss: 0.091581
Epoch: 4900, loss: 0.091581
Epoch: 5000, loss: 0.091581
Epoch: 5100, loss: 0.091581
Epoch: 5200, loss: 0.091581
Epoch: 5300, loss: 0.091581
Epoch: 5400, loss: 0.091581
Epoch: 5500, loss: 0.091581
Epoch: 5600, loss: 0.091581
Epoch: 5700, loss: 0.091581
Epoch: 5800, loss: 0.091581
Epoch: 5900, loss: 0.091581
Epoch: 6000, loss: 0.091581
Epoch: 6100, loss: 0.091581
Epoch: 6200, loss: 0.091581
Epoch: 6300, loss: 0.091581
Epoch: 6400, loss: 0.091581
Epoch: 6500, loss: 0.091581
Epoch: 6600, loss: 0.091581
Epoch: 6700, loss: 0.091581
Epoch: 6800, loss: 0.091581
Epoch: 6900, loss: 0.091581
Epoch: 7000, loss: 0.091581
Epoch: 7100, loss: 0.091581
Epoch: 7200, loss: 0.091581
Epoch: 7300, loss: 0.091581
Epoch: 7400, loss: 0.091581
Epoch: 7500, loss: 0.091581
Epoch: 7600, loss: 0.091581
Epoch: 7700, loss: 0.091581
Epoch: 7800, loss: 0.091581
Epoch: 7900, loss: 0.091581
Epoch: 8000, loss: 0.091581
Epoch: 8100, loss: 0.091581
Epoch: 8200, loss: 0.091581
Epoch: 8300, loss: 0.091581
Epoch: 8400, loss: 0.091581
Epoch: 8500, loss: 0.091581
Epoch: 8600, loss: 0.091581
Epoch: 8700, loss: 0.091581
Epoch: 8800, loss: 0.091581
Epoch: 8900, loss: 0.091581
Epoch: 9000, loss: 0.091581
Epoch: 9100, loss: 0.091581
Epoch: 9200, loss: 0.091581
Epoch: 9300, loss: 0.091581
Epoch: 9400, loss: 0.091581
Epoch: 9500, loss: 0.091581
Epoch: 9600, loss: 0.091581
Epoch: 9700, loss: 0.091581
Epoch: 9800, loss: 0.091581
Epoch: 9900, loss: 0.091581

Process finished with exit code 0