Python中的高性能科学计算基础包——Numpy

最新推荐文章于 2021-01-13 10:52:17 发布
原创 最新推荐文章于 2021-01-13 10:52:17 发布 · 667 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#python #numpy #random

本文介绍使用Python和NumPy库实现随机漫步的过程，通过创建一个初始位置为0的漫步者，进行1000步随机移动，每一步随机选择前进或后退，并展示漫步路径的数组表示。

文章目录

数组创建函数

在这里插入图片描述

ndarray的数据类型

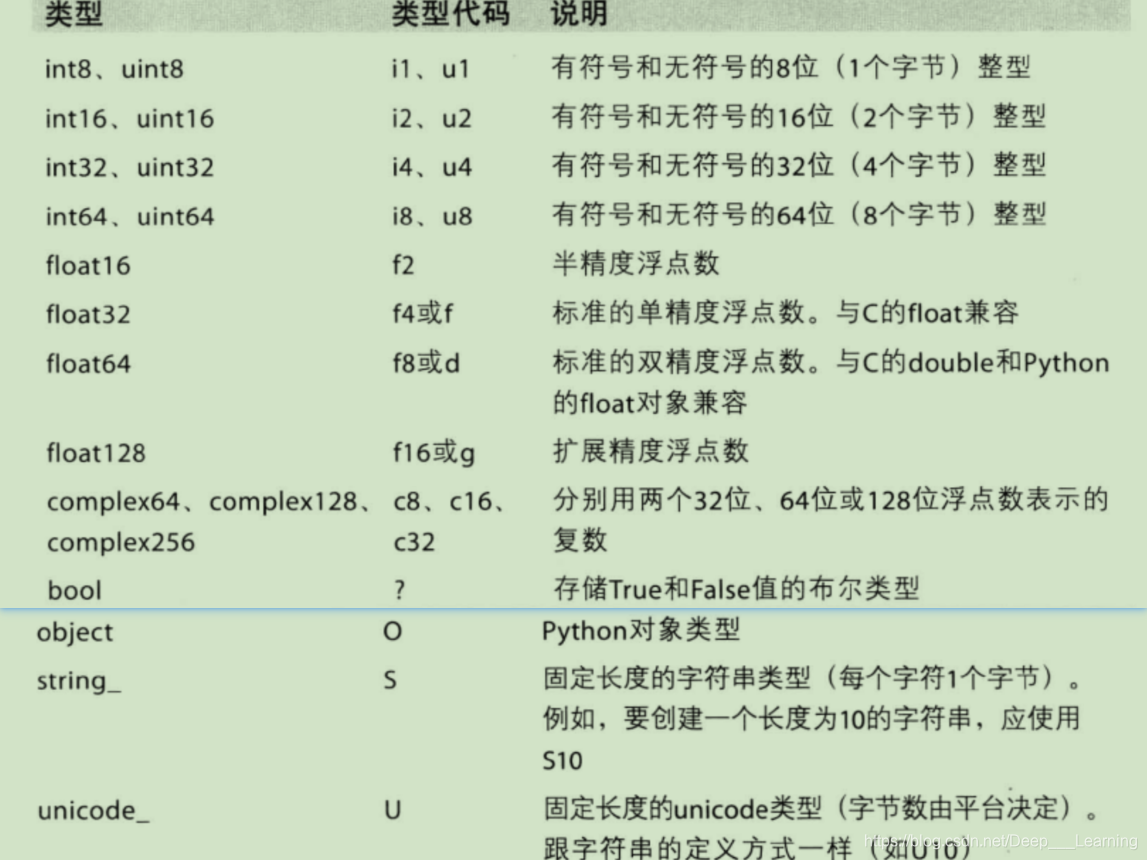
在这里插入图片描述

二维数组的索引方式

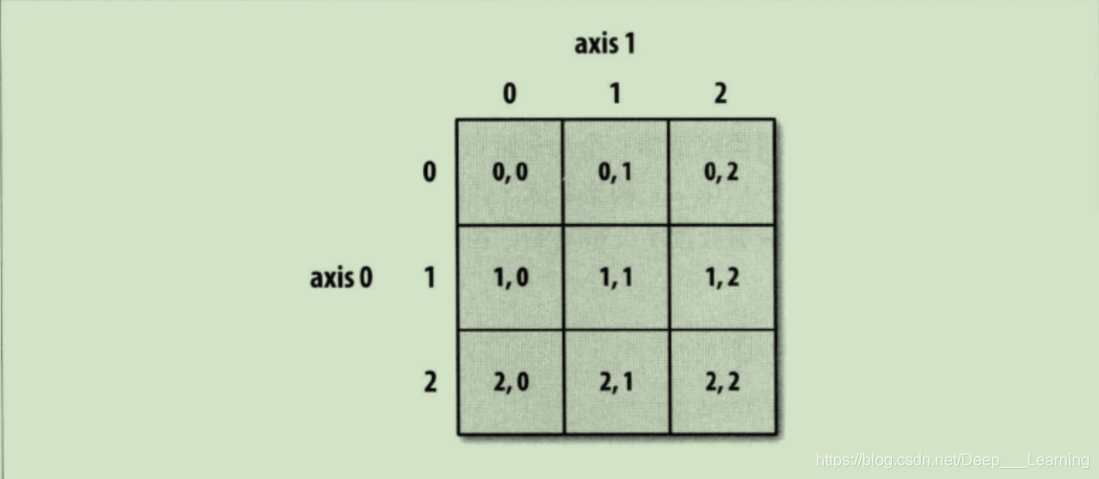
在这里插入图片描述

二维数组切片

在这里插入图片描述

通用函数

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

基本数组的统计方法

在这里插入图片描述

数组的集合运算

在这里插入图片描述

常用的线性代数函数

在这里插入图片描述

随机数

在这里插入图片描述

范例：随机漫步

import random

position = 0
walk = [position]
steps = 1000
for i in range(steps):
    step = 1 if random.randint(0,1) else -1
    position += step
    walk.append(position)

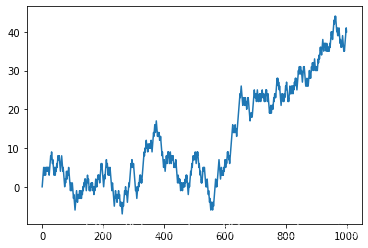
结果如下图所示：
在这里插入图片描述

nsteps = 1000
draws = np.random.randint(0,2,size=nsteps)
steps = np.where(draws>0, 1, -1)
walk = steps.cumsum()

array([  1,   2,   3,   2,   3,   4,   5,   4,   3,   4,   3,   2,   1,
         0,  -1,  -2,  -3,  -2,  -3,  -2,  -1,  -2,  -1,   0,   1,   0,
        -1,   0,  -1,   0,  -1,   0,   1,   2,   3,   4,   3,   2,   1,
         0,   1,   0,   1,   2,   3,   4,   5,   6,   7,   6,   5,   6,
         7,   6,   5,   4,   5,   4,   3,   2,   1,   2,   1,   0,  -1,
        -2,  -1,   0,   1,   2,   3,   2,   3,   4,   5,   4,   5,   4,
         5,   6,   7,   6,   5,   6,   7,   6,   7,   8,   9,   8,   7,
         8,   7,   8,   9,   8,   9,   8,   9,   8,   7,   8,   9,  10,
        11,  10,  11,  10,   9,   8,   9,   8,   9,  10,  11,  12,  13,
        14,  13,  14,  13,  12,  11,  12,  13,  12,  11,  12,  13,  14,
        13,  14,  13,  12,  13,  14,  13,  12,  11,  10,  11,  10,   9,
         8,   9,   8,   7,   6,   7,   6,   5,   6,   5,   6,   5,   4,
         5,   6,   7,   6,   5,   4,   5,   4,   3,   2,   3,   2,   1,
         2,   1,   0,   1,   2,   3,   4,   5,   6,   5,   4,   3,   2,
         1,   0,   1,   0,   1,   2,   3,   4,   3,   2,   1,   2,   1,
         2,   3,   4,   3,   2,   1,   2,   1,   0,   1,   2,   1,   0,
         1,   2,   3,   4,   5,   6,   7,   6,   7,   6,   5,   4,   3,
         4,   3,   4,   3,   4,   5,   6,   7,   6,   5,   6,   5,   4,
         3,   4,   3,   2,   3,   4,   5,   6,   5,   6,   5,   6,   7,
         8,   7,   8,   7,   8,   7,   6,   5,   6,   7,   8,   7,   8,
         7,   6,   7,   6,   7,   6,   5,   4,   3,   2,   1,   0,   1,
         0,  -1,   0,   1,   2,   1,   0,   1,   0,   1,   0,  -1,  -2,
        -1,  -2,  -1,  -2,  -3,  -2,  -3,  -4,  -5,  -6,  -5,  -4,  -3,
        -4,  -3,  -2,  -1,  -2,  -3,  -2,  -1,  -2,  -3,  -4,  -3,  -2,
        -3,  -4,  -3,  -2,  -1,  -2,  -3,  -4,  -5,  -6,  -7,  -6,  -5,
        -6,  -7,  -8,  -7,  -8,  -9,  -8,  -9,  -8,  -9,  -8,  -9, -10,
        -9, -10, -11, -10,  -9,  -8,  -9,  -8,  -7,  -8,  -9, -10, -11,
       -10, -11, -10,  -9, -10,  -9,  -8,  -9,  -8,  -9, -10,  -9,  -8,
        -9,  -8,  -7,  -8,  -7,  -8,  -9, -10,  -9,  -8,  -9,  -8,  -7,
        -6,  -5,  -4,  -3,  -4,  -3,  -4,  -5,  -4,  -5,  -4,  -3,  -4,
        -3,  -2,  -3,  -2,  -3,  -4,  -5,  -4,  -3,  -4,  -5,  -4,  -3,
        -2,  -3,  -4,  -3,  -2,  -3,  -2,  -3,  -2,  -3,  -2,  -1,   0,
        -1,  -2,  -3,  -2,  -1,  -2,  -3,  -4,  -3,  -2,  -1,  -2,  -1,
         0,   1,   2,   1,   0,   1,   0,   1,   2,   3,   4,   5,   6,
         5,   6,   7,   8,   9,  10,   9,   8,   7,   8,   7,   6,   5,
         6,   7,   6,   5,   6,   5,   6,   7,   6,   5,   6,   5,   4,
         5,   4,   3,   2,   1,   2,   1,   2,   3,   2,   3,   2,   3,
         4,   5,   6,   7,   6,   7,   8,   9,  10,  11,  10,   9,  10,
         9,  10,  11,  12,  13,  14,  13,  14,  15,  14,  13,  14,  13,
        12,  13,  14,  15,  16,  17,  18,  17,  16,  15,  16,  15,  16,
        15,  14,  13,  14,  15,  16,  15,  14,  13,  14,  13,  14,  15,
        16,  17,  18,  19,  18,  17,  16,  17,  16,  15,  14,  15,  14,
        13,  14,  15,  14,  13,  12,  13,  14,  13,  12,  13,  12,  13,
        14,  15,  16,  17,  18,  19,  20,  19,  20,  19,  20,  19,  20,
        19,  20,  19,  20,  21,  20,  21,  22,  23,  24,  25,  26,  25,
        26,  25,  26,  27,  26,  27,  28,  29,  30,  31,  30,  31,  32,
        31,  30,  29,  30,  31,  32,  31,  32,  33,  32,  31,  32,  31,
        32,  33,  32,  33,  34,  33,  34,  35,  34,  33,  34,  35,  34,
        33,  32,  31,  32,  33,  34,  35,  34,  33,  34,  35,  34,  35,
        34,  35,  34,  35,  36,  35,  34,  33,  34,  35,  34,  33,  32,
        33,  32,  31,  32,  33,  34,  33,  34,  33,  32,  31,  30,  31,
        30,  29,  30,  31,  30,  29,  28,  27,  28,  27,  26,  25,  24,
        25,  24,  25,  26,  25,  26,  25,  26,  27,  28,  27,  26,  27,
        26,  25,  26,  25,  26,  25,  24,  25,  26,  25,  26,  27,  26,
        27,  26,  25,  26,  25,  24,  25,  26,  25,  26,  27,  28,  27,
        28,  27,  28,  29,  30,  29,  28,  29,  30,  29,  28,  29,  30,
        31,  32,  31,  32,  31,  32,  31,  30,  29,  30,  29,  28,  29,
        30,  31,  30,  29,  30,  29,  30,  29,  28,  29,  28,  29,  30,
        31,  32,  33,  32,  31,  32,  33,  34,  33,  32,  31,  32,  33,
        34,  35,  34,  33,  34,  35,  34,  33,  34,  35,  36,  35,  34,
        35,  34,  33,  32,  33,  34,  33,  34,  35,  34,  33,  32,  33,
        34,  35,  34,  35,  34,  35,  34,  35,  36,  35,  34,  33,  34,
        35,  34,  35,  34,  33,  32,  33,  34,  33,  34,  33,  34,  33,
        32,  33,  34,  33,  32,  31,  32,  31,  30,  29,  30,  29,  28,
        29,  30,  29,  30,  29,  30,  31,  30,  29,  28,  29,  28,  29,
        28,  27,  28,  27,  28,  29,  30,  29,  30,  31,  32,  33,  34,
        35,  36,  37,  36,  37,  38,  39,  38,  39,  38,  37,  38,  39,
        40,  41,  40,  39,  38,  39,  38,  39,  38,  37,  38,  37,  36,
        35,  36,  35,  36,  37,  38,  37,  38,  37,  38,  39,  38,  39,
        38,  39,  40,  39,  40,  41,  42,  43,  42,  41,  40,  39,  38,
        39,  40,  39,  40,  41,  40,  39,  38,  39,  40,  41,  40,  41,
        40,  39,  40,  39,  40,  41,  42,  41,  42,  41,  40,  39,  38,
        39,  38,  37,  38,  39,  40,  39,  40,  39,  40,  39,  38,  37,
        38,  37,  38,  39,  40,  39,  38,  39,  40,  41,  40,  39,  40,
        39,  38,  37,  38,  39,  40,  41,  42,  41,  40,  39,  38,  37,
        38,  39,  38,  37,  38,  37,  38,  39,  38,  37,  36,  37,  36,
        35,  36,  35,  36,  35,  36,  37,  38,  39,  38,  37,  38],
      dtype=int32)

结果如下图所示：
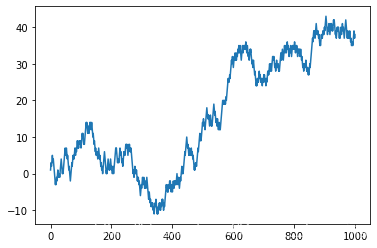
在这里插入图片描述

100天精通Python丨基础知识篇 —— 07、10个Python高级库总结
独木不成林，单弦不成音。
07-08 6万+
《C站最全Python标准库总结》，登顶了【全站综合热榜】和【python领域热榜】，获得了2362多次点赞、998次评论、2072次收藏，谢谢各位小伙伴。
详解NumPy库，强大的Python科学计算包
qq_42766267的博客
12-23 1594
哈喽，大家好。 之前写了几篇 Python 基础的文章，效果不错。为感谢大家的支持，月底搞一波抽奖送书活动。 闲话少叙，今天来详解一个 Python 库 ——NumPy。 NumPy是 Python 科学计算的基本包，几乎所有用 Python 工作的科学家都利用了NumPy的强大功能。此外，它也广泛应用在开源的项目中，如：Pandas、Seaborn、Matplotlib、scikit-learn等。 Numpy应用的领域 举个栗子，直观感下NumPy的强大。 均方差公式 上图是计算.
使用Python进行科学计算的基本软件包。-Python开发
05-24
NumPy是使用Python进行科学计算所需的基本软件包。 网站：https://www.numpy.org文档：https://numpy.org/doc邮件列表：https://mail.python.org/mailman/listinfo/numpy-discussio NumPy是科学所需的基本软件包用Python计算。 网站：https://www.numpy.org文档：https://numpy.org/doc邮件列表：https://mail.python.org/mailman/listinfo/numpy-discussion源代码：https：// github .com / numpy / numpy贡献者：https://www.numpy.org/devdocs/dev/index.html错误报告：https://github.com/numpy/numpy/issues报告安全漏洞：https：// tidelift.com/docs/security它提供：功能强大的N维数组对象sophis
Python科学计算包的基本用法
08-29
该资料是【Python数据分析与展示】课程的文档笔记，主要讲解了Numpy、Pandas、Matplotlib的基本用法及其应用举例。
Python科学计算基础包-Numpy
月吖吖
03-20 743
一、Numpy概念Numpy（Numerical Python的简称）是Python科学计算的基础包。它提供了以下功能：快速高效的多维数组对象ndarray。用于对数组执行元素级计算以及直接对数组执行数学运算的函数。用于读写硬盘上基于数组的数据集的工具。线性代数运算、傅里叶变换，以及随机数生成。用于将C、C++、Fortran代码集成到Python的工具。除了为Python提供快速的数组处理能力，...
python的一些科学计算的包
weixin_34148508的博客
02-02 600
在安装numpy这类科学计算的包的时候，pip下载的东西有时候缺少一些东西。 可以到这里下载,根据提示信息，少哪个包，或者哪个包出现错误就安装哪个包。 PIL到这里下载...
python科学计算之numpy——ufunc函数用法
09-18
Numpy（Numerical Python）是一个开源的Python扩展包，用于数值计算，它提供了高性能的多维数组对象以及这些数组的操作工具。Numpy中的ufunc（universal function，通用函数）是一类对数组进行元素级操作的函数，...
Python科学计算基础包NumPy详解
NumPy是使用Python进行科学计算所需的基础软件包，这一标题和描述准确地概括了NumPy在现代数据科学、工程计算、机器学习以及数值模拟等领域中的核心地位。作为Python生态系统中最基础且最重要的库之一，NumPy为高效...
NumPy 1.5初学者指南：Python高性能科学计算实战
资源摘要信息:"NumPy 1.5 Beginner's Guide 是一本专为初学者设计的关于 NumPy 库的详细入门指南，全书共234页，系统性地介绍了如何使用这一基于 Python 的高性能开源数学计算库进行科学计算与数据处理。该书由 Ivan...
高性能科学计算包numpy-1.13.1+mkl适用于python2.7-win64
1. **NumPy库的重要性**：NumPy是科学计算领域不可或缺的库，它为Python提供了高性能的多维数组对象以及处理这些数组的工具。由于其优化的数组操作性能，NumPy在数据分析、图像处理、物理仿真等多个领域得到广泛应用...
数据矿工学习-Python数据分析之numpy
翁JJ的博客
05-17 404
前言刚开始学习数据挖掘时，有时总是对numpy和pandas傻傻分不清楚，这个问题在训练模型阶段输入训练数据的时候最为明显，下面就来详细介绍下numpy和pandasNumpyWHAT？numpy是专门为科学计算设计的一个python扩展包，为python提供高效率的多维数组，也被称为面向阵列计算（array oriented computing），同时numpy也是github上的一个开源项目：...
Numpy学习二
lxiao428的博客
09-26 336
这是Numpy的知识点，常见的函数和操作，功能点还没有完善~~ # -*- coding: utf-8 -*- """ Created on Sun Sep 23 23:14:38 2018 @author: Lxiao217 """ ''' NumPy是使用Python进行科学计算的基础包。它包含其他内容： 一个强大的N维数组对象 复杂的（广播）功能 用于集成C / C ++和Fortra...
python科学计算的基本包_Numpy等Python科学计算包的安装与配置
weixin_39770821的博客
11-29 370
2.2 计算平台的配置本章将以Windows平台和Linux平台为例，讲解R和Python科学计算平台的配置。Python和R具有跨平台运行的特点，Windows平台编写的Python和R代码只需修正兼容性问题即可正常运行在类UNIX平台上，如：中文字符的UTF8与GBK转换、Windows系统与类UNIX平台的文件路径差异等。2.2.1 Numpy等Python科学计算包的安装与配置Python...
Python的科学计算包Numpy
xlperpetual的博客
11-23 231
一、地址与指向 import numpy as np a = np.arange(12) b = a # a和b的地址值相同 c = a.view() # a和c的地址值不同，但是指向相同 d = a.copy() # a和d的地址值不同，指向也不同 二、赋值操作 data = np.sin(np.arange(20)).reshape(5,4) 代码结果为 [[ 0. ...
Python科学计算之NumPy
weixin_34236497的博客
07-12 154
本文是我在Python程序员官方微信公众号看到的一篇文章，翻译的质量不错，也正好学习下NumPy这个数学库，所以，转载出来，如果需要了解更多的有关Python的精彩文章，请关注他们的官方公众号Python部落(python.freelycode.com）。 哦，你可以用NumPy做惊人的事情。 NumPy是Python用于处理大型矩阵的一...
python科学计算的基本包_Python科学计算基本包Numpy使用的教程
weixin_39953102的博客
11-29 399
前言Numpy是Python科学计算的基本包，它提供一个多维数组对象及各种派生对象（如屏蔽的数组和矩阵）以及一系列用于数组快速操作的例程，包括数学、逻辑、形状操作、排序、选择、I/O，离散傅里叶变换、线性代数、基本统计操作、随机模拟等等。Numpy融合了C语言的高效性和Python的简单性：像C一样快：逐个元素操作是numpy的默认模式，由预编译的C代码完成； 比Python更简单：Numpy的惯...
python科学计算的基本包是什么_Python科学计算常用的工具包有哪些?
weixin_29895109的博客
01-13 993
展开全部1、 NumPyNumPy几乎是一个无法回避的科学计算工具包，最常用的也许是它的N维数组对象，其他还包括一些成32313133353236313431303231363533e58685e5aeb931333436316238熟的函数库，用于整合C/C++和Fortran代码的工具包，线性代数、傅里叶变换和随机数生成函数等。NumPy提供了两种基本的对象：ndarray(N-dimensi...
python科学计算的基本包是什么_中国大学MOOC: Python科学计算的基本包是（ ）。...
weixin_35564436的博客
01-13 269
中国大学MOOC: Python科学计算的基本包是( )。答：numpy中国大学MOOC: 在闪耀光栅中,使刻槽面与光栅面成一定角度,目的是使_答：干涉零级与衍射零级在空间分开同一工步的划分依据是指只要在加工表面和加工工具不变的情况下都属于同一工步答：×食物蛋白质的氨基酸模式与人体蛋白质的氨基酸模式越接近说明( )。答：必需氨基酸在体内的利用率越高At the age of five, she ...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值