本文探讨了线性代数的基本概念，包括标量、向量、矩阵和张量的定义，深入讲解了矩阵乘法、单位矩阵、逆矩阵等关键操作。此外，文章还覆盖了线性相关性、子空间、范数的概念，以及特殊矩阵如对角矩阵和正交矩阵的特点。最后，介绍了特征分解、奇异值分解和Moore-Penrose伪逆等高级主题。
标量、向量、矩阵和张量
- 标量：一个标量就是一个单独的数，它不同于线性代数中研究的其他大部分对象（通常是多个数的数组）。
- 向量：一个向量是一列数。
- 矩阵：矩阵是一个二维数组，其中的每一个元素被两个索引（而非一个）所确定。
- 张量：在某些情况下，我们会讨论坐标超过两维的数组，一般地，一个数组中的元素分布在若干维坐标的规则网络中，我们称之为张量。
矩阵的乘法
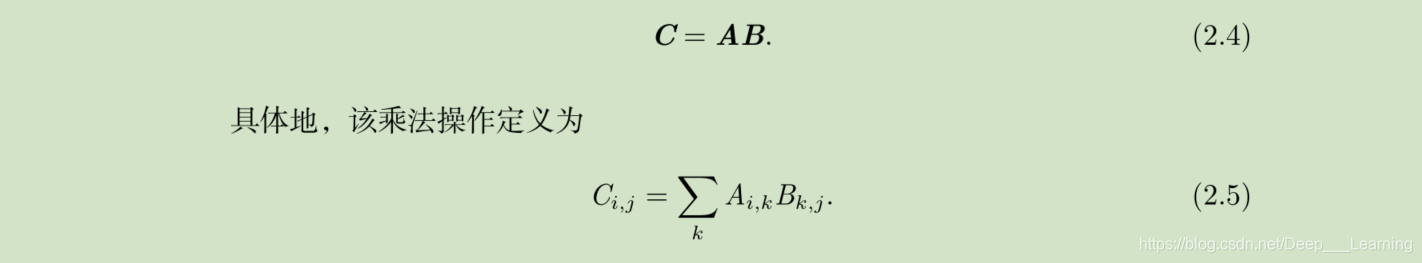
单位矩阵和逆矩阵
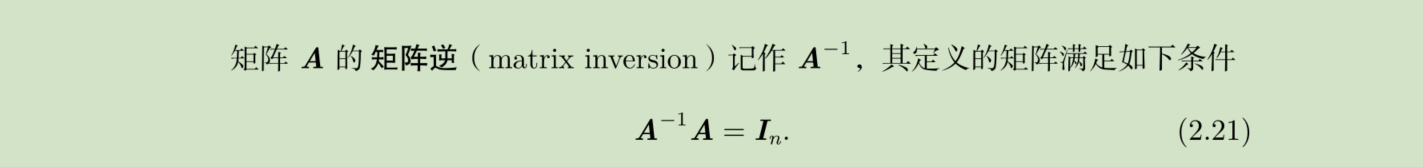
线性相关和生成子空间
如果一组向量中的任意一个向量都不能表示成其他向量的线性组合，那么这组向量称为线性无关
范数
特殊类型的矩阵和向量
- 对角矩阵：只在主对角线上含有非零元素，其他位置都是零
- 正交矩阵：行向量和列向量是分别标准正交的方阵
- 单位向量：具有单位范数的向量
特征分解
奇异值分解
Moore-Penrose伪逆
迹运算
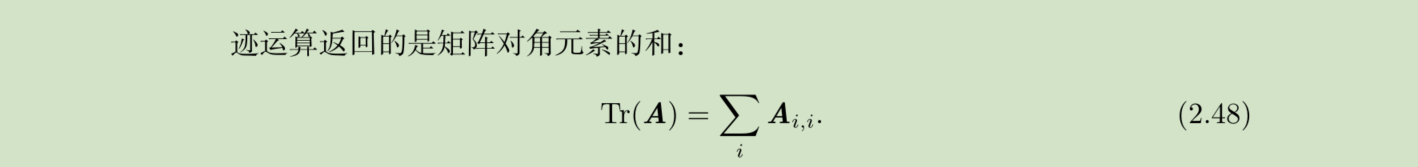
行列式
扫一扫
3764
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
