苏州省选集训营第一天题解

最新推荐文章于 2021-01-09 10:55:39 发布

原创最新推荐文章于 2021-01-09 10:55:39 发布 · 426 阅读

0 ·

CC 4.0 BY-SA版权

数论专栏收录该内容

49 篇文章

订阅专栏

正题

只补了两题，第三题是一道交互题没办法补，但还是会讲思路。

第一题：做法就是我们考虑到如果每个人都可以获胜那么i连到pi的这张有向图必定是一个环，那么我们就是要在一个环里面分配点对使得在n组点对中有k组是相邻的。由于对于每一个环的答案都是相同的，比如说(1->2->3->1,1->3->2->1)，因为分配的方案与点的顺序无关，那么我们可以只考虑一个环，假设我们考虑的环就是(1->2->3->4->...->n->1)。

我们想到有且仅有k组的答案是非常难算的，我们考虑构造一个更好算的东西。

我们设有且仅有i组的答案为 $g(i)$ ，我们设 $f(i)=2n*\frac{C_{2n-i-1}^{i-1}*\frac{(2n-2i)!}{2^{n-i}(n-i)!}}{i}$ 。

这是什么呢？其实这也是有依据的，我们假设现在有i个已经连接好的相邻的点对，然后将(2n-2i)个元素插入除了开头前的m个空档中，相当于在(2n-2i)个元素中插入(m-1)个档板，所以方案数就是 $C_{2n-2i+i-1}^{i-1}=C_{2n-i-1}^{i-1}$ ，然后我们考虑剩下的元素如何组成点对，方案数很明显为 $\frac{(2n-2i)!}{2^{n-i}(n-i)!}$ ，为什么呢？考虑2n个元素的时候我们的方案数是 $\frac{C_{2n}^2*...*C_2^2}{n!}$ ，因为不考虑顺序所以要除以n!。那么这个东西就是 $\frac{(2n)!}{2^nn!}$ ，类比一下。

接着对于每i种方案里面我们只能保留一种，因为下面两种情况是相同的。

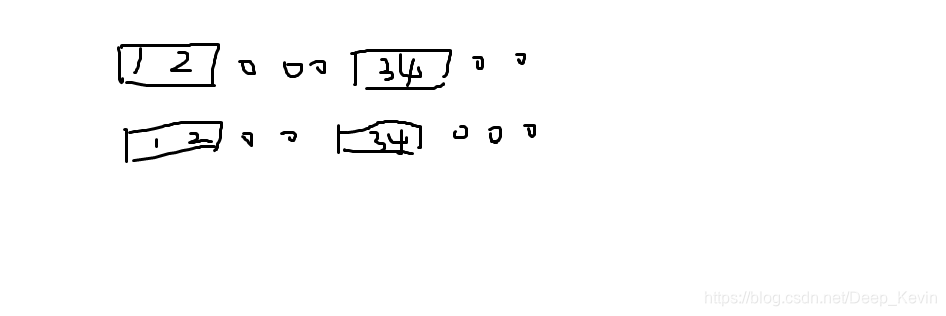
假设我们只保留第一种，然后乘上2n相当于旋转2n次每种情况就都只被算了一次了！！

而这些情况中包含上图中的第二行，所以如果不除以i会导致出现重复的情况。

接着我们考虑，对于(i>j) g(i)在f(j)内被算了 $C_i^j$ 次。

因为相当于f(j)在算的时候枚举到的恰好是g(i)中的j个点对。

所以 $f(j)=\sum_{i=j}^nC_i^j g(i)$ 。

二项式反演可以得到： $g(i)=\sum_{j=i}^n (-1)^{j-i}C_j^if(j)$ ，直接扫一遍即可，注意预处理。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
using namespace std;

int n,k;
const int maxn=2e7;
const int mod=1e9+7;
long long fac[maxn+10],inv[maxn+10];
long long back[maxn+10],pow[maxn+10];

long long ksm(long long x,long long t){
	long long tot=1;
	while(t){
		if(t&1) (tot*=x)%=mod;
		(x*=x)%=mod;
		t/=2;
	}
	return tot;
}

long long C(int x,int y){
	return fac[x]*inv[x-y]%mod*inv[y]%mod;
}

long long K(int x){
	return fac[2*x]*pow[x]%mod*inv[x]%mod;
}

long long F(int x){
	int temp=n-x;
	return 2*n*back[x]%mod*C(temp+n-1,x-1)%mod*K(temp)%mod;
}

int main(){
	scanf("%d %d",&n,&k);
	fac[0]=1;for(int i=1;i<=maxn;i++) fac[i]=fac[i-1]*i%mod;
	inv[maxn]=ksm(fac[maxn],mod-2);for(int i=maxn-1;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
	for(int i=1;i<=maxn;i++) back[i]=inv[i]*fac[i-1]%mod;
	pow[0]=1;long long tot=ksm(2,mod-2);for(int i=1;i<=maxn;i++) pow[i]=(pow[i-1]*tot)%mod;
	long long ans=0;
	if(k==0) ans=K(n);
	for(int i=max(k,1);i<=n;i++)
		(ans+=((i-k)&1?mod-1:1)*C(i,k)%mod*F(i)%mod)%=mod;
	printf("%lld\n",ans*ksm(K(n),mod-2)%mod);
}

第二题：这题做法十分的妙，我们先考虑三角形和线段可能有多少个交点。明显最多2个是吧。

那么我们设a为没有交点的方案数，b为有一个交点的方案数，c为有两个交点的方案数。

显然的 $a+b+c=C_n^3*C_{n-3}^2=\frac{n!}{12*(n-5)!}$ 。选出三个点为三角形顶点，在从剩下的点选出两个点为线段顶点。

b也是非常好求的，我们枚举一个三角形，如果在三角形内部的点共有B个，那么这个三角形的答案就是 $B*(n-3-B)$ ，因为有且仅有一个交点当且仅当一个点在三角形内部一个点在三角形外部。 $b=\sum B(n-3-B)$ 。

B怎么算呢？我们对于每一条线段求出每一个点是否在它的逆时针0~180方向，存在一个bitset里面，然后对于一个三角形 $(T_1,T_2,T_3)$ ，我们枚举三个点，然后按顺序把他们所对应线段的bitset&起来就好了。要注意的是，对于一个三角形要枚举两次，也就是说要枚举 $(T_1,T_2,T_3) \and \ (T_1,T_3,T_2)$ ，因为你不能保证三个点是否按照逆时针顺序数。

接着c怎么算呢？很难算？是的，我们直接算出总交点个数b+2c就好了。

明显的，我们选出四个点，当且仅当这四个点的凸包是4边形的时候，才会由相对顶点的连线形成一个交点，接着，这个交点会被算 $2*(n-4)$ 次，因为对于除了这四个点的其他n-4个点，可能与一条四边形的对角线形成一个三角形，这个交点就会被算一次，两条对角线所以就是 $2*(n-4)$ 。

怎么求四个点组成的凸四边形个数？我们知道选出四个点的方案数就是 $C_n^4$ ，我们只要减去那些四个点不组成凸四边形的就行了。

那么那些图形必定是三角形内有一个点，所组成的四元组，那么就是 $\sum B$ 。

所以综上：

$\\a+b+c=\frac{n!}{12*(n-5)!} \\b=\sum B(n-3-B) \\b+2c=C_n^4 - \sum B$

求出a好像挺简单的吧。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<bitset>
using namespace std;

int n;
struct node{
	int x,y;
	friend node operator-(const node a,const node b){return (node){a.x-b.x,a.y-b.y};}
}s[310];
long long ans,ans1,ans2,temp;
bitset<301> has[301][301]; 

int get_cro(node a,node b){
	return a.x*b.y-b.x*a.y;
}

int main(){
	scanf("%d",&n);
	ans=(long long)n*(n-1)*(n-2)*(n-3)*(n-4)/12;
	for(int i=1;i<=n;i++) scanf("%d %d",&s[i].x,&s[i].y);
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)	for(int k=1;k<=n;k++) if(get_cro(s[j]-s[i],s[k]-s[i])>0) has[i][j][k]=true;
	ans2=(long long)n*(n-1)*(n-2)*(n-3)/24;
	for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) for(int k=i+1;k<=n;k++) if(j!=k) {
		temp=(has[i][j]&has[j][k]&has[k][i]).count();
		ans1+=temp*(n-3-temp);
		ans2-=temp;
	}
	ans2*=2*(n-4);
	ans2-=ans1;
	ans-=ans1+ans2/2;
	printf("%lld\n",ans);
}

第三题：这题看似很难，实际很难。

首先我们先求出1到2，2到3，...，n到1的这些边是黑边还是白边。如果已经有n-1条同色边，那么结束了。

如果没有，那么必定有一个点所连的两条边是黑边和白边，所以我们先把这个点删掉，再问出来与它相邻两个点的边的颜色，为什么可以直接不考虑这个点呢？因为这个点无论经过黑边还是白边都可以走到它。接着从剩下的环里面再找，一直找到环上的同色边等于环上的点数-1时，倒过来输出一下就好了。

我没有写代码因为我tcl。