学习笔记第五十七节:回文自动机

正题

      由于回文自动机的代码十分的有趣,以至于半天都没看懂怎么实现.

      为了解决广大苦困人民的烦恼,我决定写一篇针对代码的讲解

      首先回文自动机有两个根,一个是偶根,一个是奇根.

      偶根的长度为0,奇根的长度为-1.

      为什么要这样设置?讲完前面部分再说

      首先长度表示的是当前点所对应的回文串长度,从偶根或奇根往下遍历时,在两边同时加上转移边对应的字符,这样会使回文串长度+2,当从奇根往下遍历的时候,可以发现第一步其实只将长度变为了1(奇根的长度为-1,+2后变为1)加了一个字符,这也满足了奇根管理长度为奇数的回文串的性质.

      转移边在上面已经说过了

      fail指针,与ACAM和SAM一样,PAM也有自己的fail指针,含义也大致相同,指向的是 不等于当前点本身 的 最长 回文 后缀.

      特别的,偶根的fail指针为奇根,奇根指向他自己

      算法流程与SAM一样完全在线构造:

      在pos位置加入一个字符c

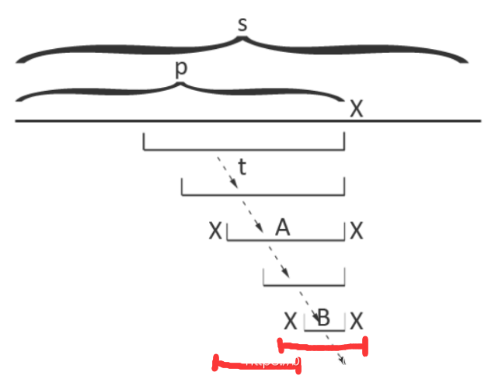
      对于pos-1最长回文后缀所对应的点,不断的跳fail,直到找到一个fail祖先p的长度,满足s[pos-len[p]-1]=s[pos],也就是说在这个p所对应的回文串两边加上一个字符c是可行的,那么就将p点记录下来,若不存在这样的p点?那么fail指针会一直跳到奇根,发现奇根一定满足上面的这条式子,所以一定可以找到一个p,至于为什么奇根一定合法?相当于本身存在

      找到这个p之后,我们看看这个点是否有儿子c,若有,啥都不用做,直接退出,因为当前必定不可能增加一个新的回文串,否则必定新增了一个回文串(所以可以想到本质不同的回文串就是总点数-2),那么新建一个点now,去找now的fail,发现now的fail去除两端之后必定是p的fail,那么我们让p去找它的fail,直到再找到一个fail祖先q满足两端同时有个c,不存在?奇根一定是答案,那么就将now的fail连向q的c儿子,若找到了这样一个不为奇根的q,那么c儿子一定存在,考虑对称性;如果找到的q为奇根?那么奇根的c儿子要么存在,要么就是偶根(编号为0).

      同时要注意,要先找fail,再连p和now的转移,因为若p是奇根,那么q也必为奇根,如果先连了转移边,那么now的fail就变成了它自己,而不是偶根.

      理解到这里,你就差不多理解了PAM,想要提高自己的理解?多去做做SAM的题把,因为PAM确实没什么题.

      

#include<bits/stdc++.h>
using namespace std;

const int N=5000010;

struct Palindrome_Automaton{
	char s[N];
	int tot,n,ch[N][26],fail[N],len[N],las,dep[N];
	void init(){tot=1;fail[0]=1;fail[1]=1;len[1]=-1;}
	int gfail(int x,int pos){
		while(s[pos-len[x]-1]!=s[pos]) x=fail[x];
		return x;
	}
	int insert(int pos,int c){
		int p=gfail(las,pos);
		if(!ch[p][c]){
			int now=++tot;
			len[now]=len[p]+2;
			fail[now]=ch[gfail(fail[p],pos)][c];
			dep[now]=dep[fail[now]]+1;ch[p][c]=now;
		}
		las=ch[p][c];
		return dep[las];
	}
	void build(){
		init();
		scanf("%s",s+1);n=strlen(s+1);
		int las=0;
		for(int i=1;i<=n;i++) {
			s[i]=(s[i]-97+las)%26+97;
			printf("%d ",las=insert(i,s[i]-'a'));
		}
	}
}PAM;

int main(){
	//freopen("P5496_1.in","r",stdin);
	//freopen("model.out","w",stdout);
	PAM.build();
}