Machine Learining（李宏毅2020） —— hw02

Machine Learining —— hw02：Logistic

1、hw02作业理解

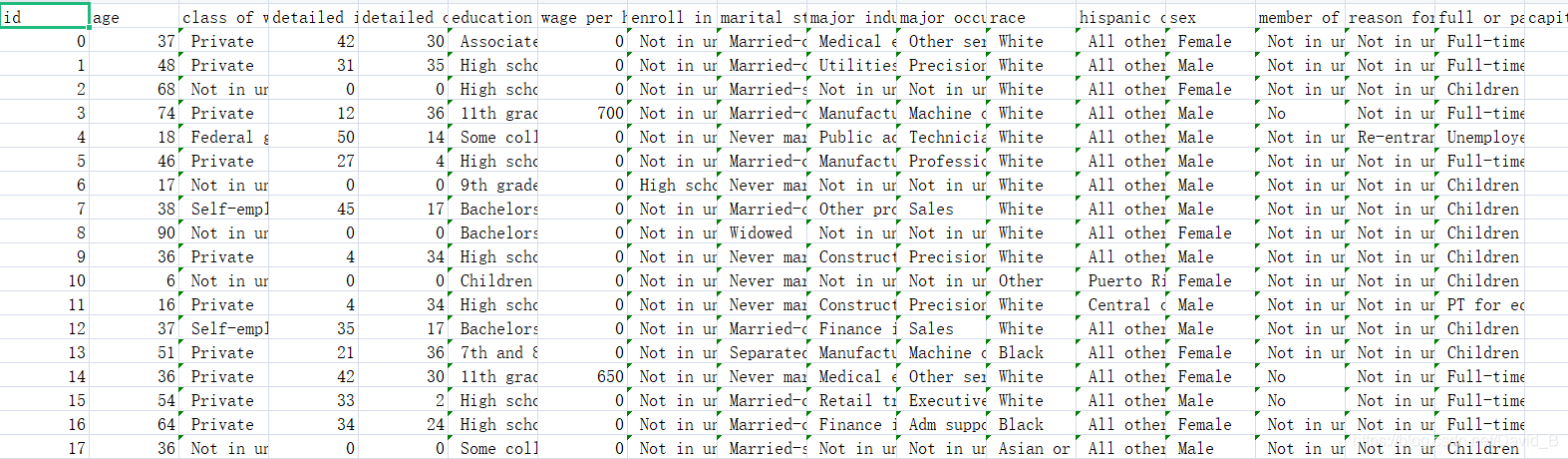
作业中共给了6份资料：输出结果格式、测试集（不带标签）、训练集、X_train、Y_train、X_test。观察可知后三个文件是已事先把数据整理成csv格式的数据，于是训练数据共54256个，测试大约20000个、参数510个

• 二分类问题（Binary Classification）
• 模型输入510维，输出一个布尔值表示“是”或“否”

——使用Logistic Regression model

2、数据预处理

读取数据

##读取文件
import numpy as np

np.random.seed(0)
#随机种子（暂未弄懂）
X_train_fpath = './hw2/data/X_train'
Y_train_fpath = './hw2/data/Y_train'
X_test_fpath = './hw2/data/X_test'
output_fpath = './output_{}.csv'

X_train、Y_train、X_test三个文件夹已经将数据进行了初步处理，可用Notepad++打开

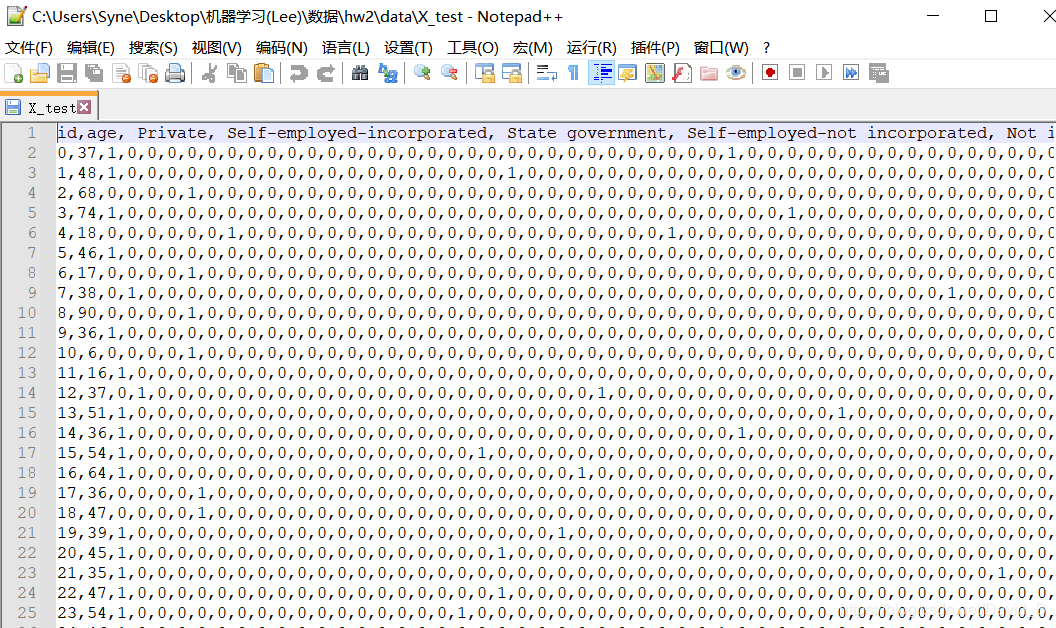
打开后通过观察可以得到，第一行是表头信息，数据之间用逗号隔开，读取数据但是第一行和第一列不需要

#Parse csv files to numpy array
with open(X_train_fpath) as f:
    next(f)
    #f文件是可迭代对象，此处调用一次跳过文件的第一行
    X_train = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)
    #按行读取数据line.strip('\n').split(',')删除数据中的换行符，遇到','就隔开
with open(Y_train_fpath) as f:
    next(f)
    Y_train = np.array([line.strip('\n').split(',')[1] for line in f], dtype = float)
    #此处Y_train文件的处理不一样（因为第一次复制粘贴前一句的代码导致Y_train数据格式不一致找了半天bug）
with open(X_test_fpath) as f:
    next(f)
    X_test = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)

Normalize处理

对X_train和X_test分别调用函数完成标准化

符号解释：

• X：将被处理的数据
• train：当处理训练集数据是为"True"，处理测试集数据时为"Flase"
• specific_column：被标准化处理的列的索引值，如果是"None"，则所有的列都将被处理
• X_mean：训练集数据的均值
• X_std：训练集数据的方差

#Normalize处理
def _normalize(X, train = True, specified_column = None, X_mean = None, X_std = None):
    #利用此函数对x进行标准化处理，均值（mean）和方差（std）将在数据处理过程中计算
    if specified_column == None:
        specified_column = np.arange(X.shape[1])
        #X.shape[1]：X的列数
        #np.arange()函数输出列的ID:[0 1 2 3 4 5......]
    
    if train:
        X_mean = np.mean(X[:, specified_column], 0).reshape(1, -1)
        X_std = np.std(X[:, specified_column], 0).reshape(1, -1)
        #np.mean(X, 0)对列求平均
        #reshape(1, -1)转化为1行
        
    X[:, specified_column] = (X[:, specified_column] - X_mean) / (X_std + 1e-8)
    #1e-8防止除零
    
    return X, X_mean, X_std

#调用函数标准化训练数据和测试数据
X_train, X_mean, X_std = _normalize(X_train, train = True)
X_test, _, _ = _normalize(X_test, train = False, specified_column = None, X_mean = X_mean, X_std = X_std)
#用 _ 存储无用值
#用X_train的均值和方差来标准化X_test???（未懂）

分割X_train为测试集和验证集

对原来的X_train进行分割，分割比例为train：dec = 9:1

#分割测试集和验证集
def _train_dev_split(X, Y, dev_ratio = 0.25):
    train_size = int(len(X) * (1 - dev_ratio))
    return X[: train_size], Y[: train_size], X[train_size:], Y[train_size:]
    #返回分割好的四组数据
    
#调用分割函数
dev_ratio = 0.1
X_train, Y_train, X_dev, Y_dev = _train_dev_split(X_train, Y_train, dev_ratio = dev_ratio)

train_size = X_train.shape[0] #求得行数
dev_size = X_dev.shape[0]
test_size = X_test.shape[0]
data_dim = X_train.shape[1]   #求得列数
print('Size of training set: {}'.format(train_size))
print('Size of development set: {}'.format(dev_size))
print('Size of testing set: {}'.format(test_size))
print('Dimension of data: {}'.format(data_dim))

output:
Size of training set: 48830
Size of development set: 5426
Size of testing set: 27622
Dimension of data: 510

3、Logistic Regression

定义一些数据处理函数

• _shuffle(X,Y)：X和Y是两个数组，如果分别随机打乱X和Y，那么X和Y的对应关系就会被破坏，在此生成行编号，对行的编号进行打乱，就可以获得一一对应的打乱后的X和Y
• _sigmoid(z)：$\sigma (z)$函数
• _np.clip(a, x1, x2)：其中a是数组，x1和x2分别表示最大值和最小值，将最小值前的数字都改成最小值，最大值后的数字都改成最大值
• _f(X, w, b)：Logistic Regression函数$f_{w,b}(X)=\sigma (wx+b)$，参数是w和b
• _predict(X, w, b)：根据X，w，b的值，计算预测值y
• np.round()：返回四舍五入值，
• _accuracy(Y_pred, Y_label)：预测精度，如：
  Y_label = 0, Y_pred = 0, 1 - |$Y_{pred}-Y_{label}$| = 1, 预测正确
  Y_label = 0, Y_pred = 1, 1 - |$Y_{pred}-Y_{label}$| = 0, 预测错误

def _shuffle(X, Y):
   #“洗牌”函数，打乱元素
   randomize = np.arange(len(X))
   #获取x的行数组成一组数列：[0 1 2 ......]
   np.random.shuffle(randomize)
   #随机打乱行数，但是各行X和Y仍是对应的
   return (X[randomize], Y[randomize])

def _sigmoid(z):
   return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1 - (1e-8))
   #计算z的sigmoid，将数组中元素限制在（1e-8, 1 - (1e-8)）之间，防溢出
   
def _f(X, w, b):
   return _sigmoid(np.matmul(X, w) + b)
   #np.matmul(X，w)矩阵乘法
   
def _predict(X, w, b):
   return np.round(_f(X, w, b)).astype(np.int)
   #round()四舍五入后，astype(np.int)转换为整型
   
def _accuracy(Y_pred, Y_label):
   acc = 1 - np.mean(np.abs(Y_pred - Y_label))
   #abs()取绝对值
   return acc

Loss Function

第n个训练数据为$(x^n,{\hat{y}}^n),x^n=[x_1^n,x_2^n,...,x_i^n,...]$（$x^n$表示第n个训练数据）

预测值 $y^n=f_{w,b}(x^n)=\sigma (w{x}^n+b)=\frac{1}{1+e^{-(w{x}^n+b)}}=\frac{1}{1+e^{-(\sum w_i{x}_i^n+b)}}=\sigma (z)$

$w^{\ast },b^{\ast }=arg\underset{w,b}{\max }L(w,b)=arg\underset{w,b}{\min }(-lnL(w,b))$

对Logistic Regression的损失函数$L(f)$取对数ln并乘以-1。

最优参数