程序设计思维与实践 Week11 Blog

一、大纲

本周作业与实验题目如下：

• 必做题11-1
• 必做题11-2
• 必做题11-3
• 必做题11-4

二、逐个击破

1.必做题11-1

题目描述

  蒜头君从现在开始工作，年薪 N 万。他希望在蒜厂附近买一套 60 平米的房子，现在价格是 200 万。假设房子价格以每年百分之 K 增长，并且蒜头君未来年薪不变，且不吃不喝，不用交税，每年所得 N 万全都积攒起来，问第几年能够买下这套房子？（第一年年薪 N 万，房价 200 万）

1. Input

  一行，包含两个正整数 $N(10\le N\le 50)$，$K(1\le K\le 20)$，中间用单个空格隔开。

2. Output

  如果在第 20 年或者之前就能买下这套房子，则输出一个整数 M，表示最早需要在第 M 年能买下；否则输出"Impossible"。

题目分析

  这道题目非常的浅显易懂了，作为一道简单的数学应用题，但是要用计算机的思维方式去思考，只需要将每一年收入的增加和房价的增加后的总和依次比较20年即可，不要用传统的数学解方程的思想去解决，那样可能确实会快，但是不利于计算思维的形成。
  题目的全部代码如下：

#include<iostream>
using namespace std;
double N,K;
double cost=200;
int main()
{
	scanf("%lf%lf",&N,&K);
	double sum=N;
	for(int i=1;i<=20;i++)
	{
		if(sum>=cost)
		{
			printf("%d",i);
			return 0;
		}
		else
		{
			cost+=(K/100)*cost;
			sum+=N;
		 } 
	}
	printf("Impossible");
	return 0;
 } 

2.必做题11-2

题目描述

  蒜头君的班级里有 $n^2$个同学，现在全班同学已经排列成一个 n * n 的方阵，但是老师却临时给出了一组新的列队方案,为了方便列队，所以老师只关注这个方阵中同学的性别，不看具体的人是谁,这里我们用 0 表示男生，用 1 表示女生,现在蒜头君告诉你同学们已经排好的方阵是什么样的，再告诉你老师希望的方阵是什么样的。他想知道同学们已经列好的方阵能否通过顺时针旋转变成老师希望的方阵

• 不需要旋转则输出 0
• 顺时针旋转 90° 则输出 1
• 顺时针旋转 180° 则输出 2
• 顺时针旋转 270° 则输出 3

若不满足以上四种情况则输出 -1，若满足多种情况，则输出较小的数字

1. Input

  第一行为一个整数 n
  接下来的 n行同学们已经列好的 01 方阵；
  再接下来的 n 行表示老师希望的的 01 方阵。

2. Output

  输出仅有一行，该行只有一个整数，如题所示。

题目分析

  这个题目值得积累，因为对于矩阵的旋转操作在平常线性代数的运算中是不涉及的，因为并没有数学意义，但是对于一些情形的直观化理解和转化，矩阵的旋转却是值得探究的，所以这里对于矩阵的旋转进行一个详细的阐述。
  首先我们来考虑矩阵顺时针旋转90度的情况：随机设置一个没有旋转的矩阵如图所示。

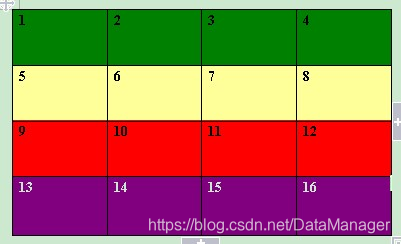
  将上述矩阵旋转90度的结果如下图所示：

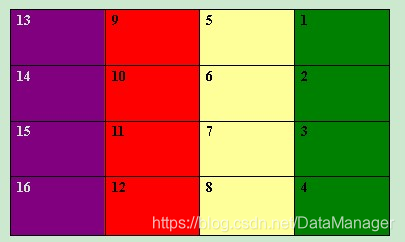
  不难发现，从行的角度考虑,原矩阵的第一行变为了新矩阵的最后一列，原矩阵的第二行变为了新矩阵的倒数第二列，以此类推。从列的角度考虑，原矩阵的第一列变为了新矩阵的第一行，数字方向相反，原矩阵的第二列变为了新矩阵的第二行，数字方向相反，以此类推。这样我们便可以根据规律进行矩阵的旋转操作了，具体代码如下：

bool rotation1()
#include<iostream>
using namespace std;
const int N=25;
int teach[N][N],sdt[N][N];
int n;
bool still()
{
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(sdt[i][j]!=teach[i][j])return false;	
	return true;
 } 

bool rotation1()
{//判定顺时针旋转90 
	int dst=n;
	for(int i=1;i<=n;i++,dst--)
		for(int j=1;j<=n;j++)
			if(sdt[i][j]!=teach[j][dst])
				return false;	
	return true;
}

bool rotation2()
{//判定顺时针旋转180度
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(sdt[i][j]!=teach[n+1-i][n+1-j])return false;
	return true;	
}

bool rotation3()
{//判定逆时针旋转90度
	int dst=1;
	for(int i=1;i<=n;i++,dst++)
		for(int j=1;j<=n;j++)
			if(sdt[i][j]!=teach[n+1-j][dst])return false;
	return true;	 
}

int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)scanf("%d",&sdt[i][j]);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)scanf("%d",&teach[i][j]);
	if(still())printf("0");
	else if(rotation1())printf("1");
	else if(rotation2())printf("2");
	else if(rotation3())printf("3");
	else printf("-1");
	return 0;
 } 

3.必做题11-3

题目描述

  Julius Caesar 曾经使用过一种很简单的密码。对于明文中的每个字符，将它用它字母表中后 55 位对应的字符来代替，这样就得到了密文。比如字符’A’用’F’来代替。如下是密文和明文中字符的对应关系。
  密文$\text{A B C D E F G H I J K L M N O P Q R S T U V W X Y Z}$
  明文$\text{V W X Y Z A B C D E F G H I J K L M N O P Q R S T U}$
  你的任务是对给定的密文进行解密得到明文。
  你需要注意的是，密文中出现的字母都是大写字母。密文中也包括非字母的字符，对这些字符不用进行解码。

1. Input

  一行，给出密文，密文不为空，而且其中的字符数不超过 200。

2. Output

  输出一行，即密文对应的明文。
  输出时每行末尾的多余空格，不影响答案正确性

题目分析

   这道题目也较为简单，主要锻炼自己能不能在尽可能短的时间内保证简单题目的正确性，不要因为一些低级错误导致丢失分数。这道题目只需要将发生循环的几个密码字母进行分类讨论即可，即对于$str[i]{<}^{\prime }{F}^{\prime }$的情况，在转化的时候要向后推算21个。

   所以这道题目具体的代码如下：

#include<stdio.h>
#include<cstring> 
using namespace std;
const int N = 205;
char str[N];
int main()
{
	gets(str);//注意这个函数只能读取保证一行不超过255个字符，否则错误 
	for(int i=0;i<strlen(str);i++)
	{
		if(str[i]>'Z'||str[i]<'A')
		{
			printf("%c",str[i]);
			continue;
		}
		else
		{
			if(str[i]>='F')
				 printf("%c",str[i]-5);
			else
				printf("%c",str[i]+21);
		}
	}
	return 0;
 } 

4.必做题11-4

题目描述

  东东和他的女朋友(幻想的)去寿司店吃晚餐(在梦中)，他发现了一个有趣的事情，这家餐厅提供的 n 个的寿司被连续的放置在桌子上 (有序)，东东可以选择一段连续的寿司来吃
  东东想吃鳗鱼，但是东妹想吃金枪鱼。核 平 起 见，他们想选择一段连续的寿司（这段寿司必须满足金枪鱼的数量等于鳗鱼的数量，且前一半全是一种，后一半全是另外一种）我们用1代表鳗鱼，2代表金枪鱼。
  比如，[2,2,2,1,1,1]这段序列是合法的，[1,2,1,2,1,2]是非法的。因为它不满足第二个要求。
  东东希望你能帮助他找到最长的一段合法寿司，以便自己能吃饱。

1. Input

  第一行：一个整数n（2≤n≤100000），寿司序列的长度。
  第二行：n个整数（每个整数不是1就是2，意义如上所述）

2. Output

  输出：一个整数（代表东东可以选择的最长的一段连续的且合法的寿司）

题目分析

   这道题目回顾了先前学习的尺取法，因为题目特征非常明显，所求答案为一个连续的区间，而且依据判断条件动态调整左右指针进行移动。尺取法的时间复杂度为 $O(n)$ ,是解决连续区间问题非常经典的方法。至于具体的实现方法稍微有些区别，这里借助一个 $chanp$ 变量用于记录当前尺取区间中包括两种🐟还是一种🐟，从而衡量两侧的鱼是否满足数量的相等以及是否可以继续扩展，然后不断记录当前最大的解，知道遍历结束便可以得到最终答案。

   所以这道题目具体的代码如下：

#include<stdio.h>
#include<cstring> 
using namespace std;
const int N = 1e5+10;
int a[N];
int n,suml,sumr,max_cnt;

void find_max()
{//采用尺取法
	int l=0,r=0;
	int chanp=-1;
	for(int i=0;i<n;i++)
	{
		
		if(a[i]==a[l] && chanp<=l)suml++;
		else if(a[i]!=a[l] && chanp<=l)
		{
			chanp=i;
			sumr++;
		}
		else if(a[i]==a[l] && chanp>l)
		{
			max_cnt=sumr>max_cnt?sumr:max_cnt;
			l=r=i;
			suml=sumr=0;
			i--;
		}
		else
		{
			if(sumr<suml)sumr++;
			else 
			{
				max_cnt=suml>max_cnt?suml:max_cnt;
				l=r=chanp;
				suml=sumr=0;
				i=chanp-1;
			}
		}
		if(i==n-1)max_cnt=sumr>max_cnt?sumr:max_cnt;
	 } 
}

int main()
{
	scanf("%d",&n);
	for(int i=0;i<n;i++)scanf("%d",&a[i]);
	find_max();
	printf("%d",max_cnt*2);
	return 0;
 }