本文深入解析单调栈与单调队列在解决典型算法问题中的应用，包括直方图最大矩形、TT’sMagicCat资产价值调整、平衡字符串最小替换长度及滑动窗口最值计算。通过实例讲解，探讨数据结构的高效使用，降低时间复杂度。
一、大纲
本周作业与实验题目如下：
- 直方图最大矩形（单调栈）
- TT’s Magic Cat （差分思想）
- 平衡字符串（尺取法与前缀和思想）
- 滑动窗口（单调队列）
二、逐个击破
1.直方图最大矩形
题目描述
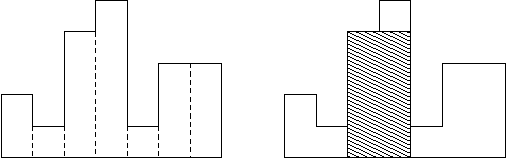
如上图所示，给一个直方图，求直方图中的最大矩形的面积。例如，下面这个图片中直方图的高度从左到右分别是2, 1, 4, 5, 1, 3, 3, 他们的宽都是1，其中最大的矩形是阴影部分。
- Input
输入包含多组数据。每组数据用一个整数n来表示直方图中小矩形的个数，你可以假定1 <= n <= 100000. 然后接下来n个整数h1, …, hn, 满足 0 <= hi <= 1000000000. 这些数字表示直方图中从左到右每个小矩形的高度，每个小矩形的宽度为1。 测试数据以0结尾。
- Output
对于每组测试数据输出一行一个整数表示答案。
题目分析
在解决问题之前，先介绍一种新的数据结构——单调栈，搞清楚它的功能以及这样的功能为什么适合解决这个问题。
- 背景
在解决很多编程问题的时候我们经常有这样的需求，在一个序列中找到每个元素左侧/右侧第一个比他大/小的元素。我们发现，如果序列是有序的，那么对于单个元素的查找可以利用二分法，其时间复杂度为O(logn)O(logn)O(logn)，对于n个元素复杂度则为O(nlogn)O(nlogn)O(nlogn);如果序列是无序的，复杂度则会更高，是否存在一种数据结构可以降低这种需求的复杂度？ - 单调
- 单调递增 1,2,3,4,51,2,3,4,51,2,3,4,5
- 单调递减 5,4,3,2,15,4,3,2,15,4,3,2,1
- 单调非增 3,2,2,1,13,2,2,1,13,2,2,1,1
- 单调非减 1,1,2,2,31,1,2,2,31,1,2,2,3 - 栈（FILO的数据结构）
单调栈 = 栈内元素自栈顶到栈底满足单调性
以单调递增栈为例:
入栈条件： 栈为空或者栈顶元素大于入栈元素
否则，元素入栈将会破坏栈的单调性，则需要将不满足条件的栈顶元素弹出后，再将元素入栈。
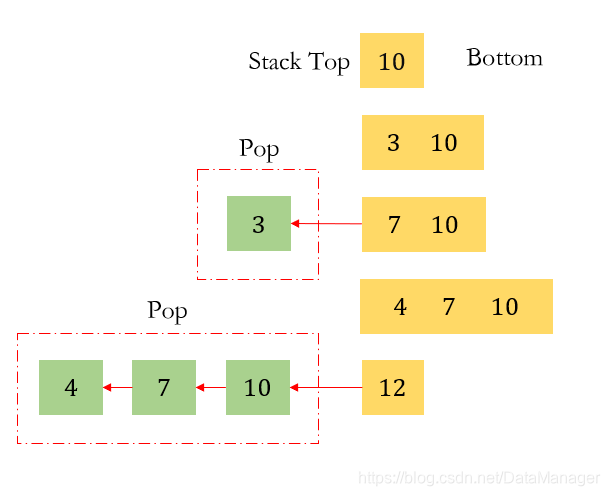
下面以[10,3,7,4,12][10,3,7,4,12][10,3,7,4,12]自左向右依次入单调递增栈为例模拟弹出栈和压入栈的情况：（如下图所示）
• 10 入栈时,栈空,入栈
• 3 入栈时,栈顶元素10 大于3,入栈
• 7入栈时,栈顶元素3 小于7,弹栈;栈顶元素10 大于7,入栈
• 4入栈时,栈顶元素7 大于4,入栈
• 12 入栈时,栈顶元素4 小于12,弹栈;栈顶元素7 小于12,弹栈;栈顶元素10 小于12,弹栈;栈空,入栈
由于每一个元素只会入栈或出栈一次，这样对于n个元素查找的时间复杂度仅为O(n)O(n)O(n)。
综上所述，单调栈的这种特性恰好适合于我们这道题的情况，我们想要找到每一个横坐标xix_ixi对应的最大矩形，也就是找xi⟶yix_i\longrightarrow y_ixi⟶yi左侧和右侧第一个比yiy_iyi小的位置然后用于计算面积SSS，单调栈代码如下：
void findR()
{
int l = 1, r = 0;//需要满足R-L+1=0
//l为栈底，r是栈顶
for(int i=1;i<=n;i++)
{
while(l <= r && a[st[r]] > a[i])
{//st[r]是栈顶元素的下标
R[st[r]] = i-1;
r--;
}
st[++r] = i;
}
int index = st[r];
while(r>=0)
{
R[st[r]] = index;
r--;
}
}
void findL()
{
int l = 1, r = 0;//需要满足R-L+1=0
for(int i=n;i>=1;i--)
{
while(l <= r && a[st[r]] > a[i])
{//st[l]是栈底元素的下标
L[st[r]] = i+1;
r--;
}
st[++r] = i;
}
int index = st[r];
while(r>=0)
{
L[st[r]] = index;
r--;
}
}
}
然后依次计算矩形大小取最大值即可，本题目的实现代码如下：
#include<iostream>
using namespace std;
const int N = 1e5+100;
int n;
long long a[N],R[N],L[N],st[N];
//a数组为每个条的高度
//R[i]、L[i]是下标为i元素能够延伸的最远的位置下标
//st[r]是栈顶元素的下标
void findR()
{
int l = 1, r = 0;//需要满足R-L+1=0
//l为栈底，r是栈顶
for(int i=1;i<=n;i++)
{
while(l <= r && a[st[r]] > a[i])
{//st[r]是栈顶元素的下标
R[st[r]] = i-1;
r--;
}
st[++r] = i;
}
int index = st[r];
while(r>=0)
{
R[st[r]] = index;
r--;
}
}
void findL()
{
int l = 1, r = 0;//需要满足R-L+1=0
for(int i=n;i>=1;i--)
{
while(l <= r && a[st[r]] > a[i])
{//st[l]是栈底元素的下标
L[st[r]] = i+1;
r--;
}
st[++r] = i;
}
int index = st[r];
while(r>=0)
{
L[st[r]] = index;
r--;
}
}
int main()
{
while(1)
{
long long max=0;
long long S;
scanf("%d",&n);
if(n==0) return 0;
else
{
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
}
getchar();
findR();
findL();
for(int i=1;i<=n;i++)
{
S=a[i]*(R[i]-L[i]+1);
if(S>max) max=S;
}
printf("%lld\n",max);
}
}
}
2.TT’s Magic Cat
题目描述
Thanks to everyone’s help last week, TT finally got a cute cat. But what TT didn’t expect is that this is a magic cat.
One day, the magic cat decided to investigate TT’s ability by giving a problem to him. That is select n cities from the world map, and a[i]a[i]a[i] represents the asset value owned by the i-th city.
Then the magic cat will perform several operations. Each turn is to choose the city in the interval [l,r][l,r][l,r] and increase their asset value by ccc. And finally, it is required to give the asset value of each city after qqq operations.
- Input
The first line contains two integers n,q(1≤n,q≤2⋅105)n,q (1≤n,q≤2⋅105)n,q(1≤n,q≤2⋅105) — the number of cities and operations.
The second line contains elements of the sequence a: integer numbers a1,a2,…,an (−106≤ai≤106)(−10^6≤ai≤10^6)(−106≤ai≤106).
Then q lines follow, each line represents an operation. The i-th line contains three integers l,rl,rl,r and ccc (1≤l≤r≤n,−105≤c≤105)(1≤l≤r≤n,−10^5≤c≤10^5)(1≤l≤r≤n,−105≤c≤105) for the i-th operation.
- Output
Print nnn integers a1,a2,…,ana1,a2,…,ana1,a2,…,an one per line, and ai should be equal to the final asset value of the i-th city.
题目分析
由题意知，每次在区间 [l,r][l,r][l,r] 上所有元素都加上数值 cic_ici ,进行 qqq 次操作，如果按照暴力做法每次对于区间上的数值赋值，时间复杂度为 O(∑n=1qciq)O(\sum_{n=1}^qc_iq)O(∑n=1qciq) ,这样对于该题的数据规模是超时的，所以必须降低算法的复杂度，鉴于这种需求我们提出了差分思想的解决方法。
设原数组为 AAA ,差分数组为 BBB ,差分数组的构造方法：
B[1]=A[1]B[1]=A[1]B[1]=A[1]
B[i]=A[i]−A[i−1]B[i]=A[i]-A[i-1]B[i]=A[i]−A[i−1]
差分数组的性质为：
1. B数组前缀和等价于A数组元素值，即
∑1iB[i]=A[i]\sum_1^i{B[i]}=A[i]∑1iB[i]=A[i]
2. A数组的区间加等价于B数组的单点修改,即
A[l]+c∼A[r]+c⇔B[l]+c，B[r+1]−cA[l]+c\sim A[r]+c\Leftrightarrow B[l]+c，B[r+1]-cA[l]+c∼A[r]+c⇔B[l]+c，B[r+1]−c
差分数组利用数组相邻元素的差值保留了从最后一个元素到第一个元素数值的回溯性，同时对于数组中连续下标的内容执行相同的操作时可以由A数组区间的修改简化为B数组单点的修改，从而降低时间复杂度为O(n+q)O(n+q)O(n+q),差分数组构造代码如下：
for(int i=1;i<=n;i++)
{//初始化差分数组
if(i==1)
{
scanf("%lld",&a[i]);
pre = a[i];
}
else
{
scanf("%lld",&tmp);
a[i] = tmp - pre;
pre = tmp;
}
}
getchar();
区间数值增加函数如下（差分数组的单点修改）
void solve(int l,int r,int num)
{
a[l]+=num;
if(r != n) a[r+1] -=num;
return ;
}
综上所述，该题全部解决代码如下：
#include<iostream>
#include<math.h>
#include<string.h>
using namespace std;
const int N = 2*1e5+50;
long long a[N];//a为差分数组
long long pre,tmp;//Attention int数据类型会爆精度
int n,q,l,r,num;
void solve(int l,int r,int num)
{
a[l]+=num;
if(r != n) a[r+1] -=num;
return ;
}
int main()
{
scanf("%d%d",&n,&q);
getchar();
for(int i=1;i<=n;i++)
{//初始化差分数组
if(i==1)
{
scanf("%lld",&a[i]);
pre = a[i];
}
else
{
scanf("%lld",&tmp);
a[i] = tmp - pre;
pre = tmp;
}
}
getchar();
for(int i=0;i<q;i++)
{
scanf("%d%d%d",&l,&r,&num);
getchar();
solve(l,r,num);
}
long long sum=0;
for(int i = 1;i<=n;i++)
{
if(i == n)
{
printf("%lld",a[i]+sum);
sum+=a[i];
}
else
{
printf("%lld ",a[i]+sum);
sum+=a[i];
}
}
return 0;
}
Tips:
这道题当时做完以后一直WA，因为int爆精度了，后来经过求助才知道需要换为long long数据类型才可以，这个点以后一定要注意，以及printf中输出long long类型数据使用%lld
3.平衡字符串
题目描述
一个长度为 n 的字符串 s，其中仅包含 ‘Q’, ‘W’, ‘E’, ‘R’ 四种字符。(1<=n<=10^5,n是4的倍数)
如果四种字符在字符串中出现次数均为 n/4，则其为一个平衡字符串。
现可以将 s 中连续的一段子串替换成相同长度的只包含那四个字符的任意字符串，使其变为一个平衡字符串，问替换子串的最小长度?
如果 s 已经平衡则输出0。
- Input
一行字符表示给定的字符串s
- Output
一个整数表示答案
题目分析
这道题目的解决方法使用到了尺取法和前缀和的思想，下面首先介绍尺取法的使用。尺取法又称双指针法，是一种数组上的常用操作，适用于以下情况：
- 解决所求解答案在一个连续的区间。（当然很多问题可以通过排序等方式将不连续转化为连续区间的问题）
- 区间的左、右端点移动方向明确。
下面以例题来说明尺取法的使用：
长度为n的数组，每个数均为正整数，给出正整数S，要求在O(n)O(n)O(n)复杂度内求出满足S≤S\leqS≤区间和的最小区间长度
- 数组为[5,1,3,5,10,7,4,9,2,8],S=15[5,1,3,5,10,7,4,9,2,8],S=15[5,1,3,5,10,7,4,9,2,8],S=15，双指针操作过程如下图所示，
如果sum⩾Ssum\geqslant Ssum⩾S，更新答案且L++L++L++
如果sum<Ssum< Ssum<S，R++R++R++
如果sum=Ssum= Ssum=S，L++L++L++而且R++R++R++(这里是个小细节要注意)
处理过程如下：
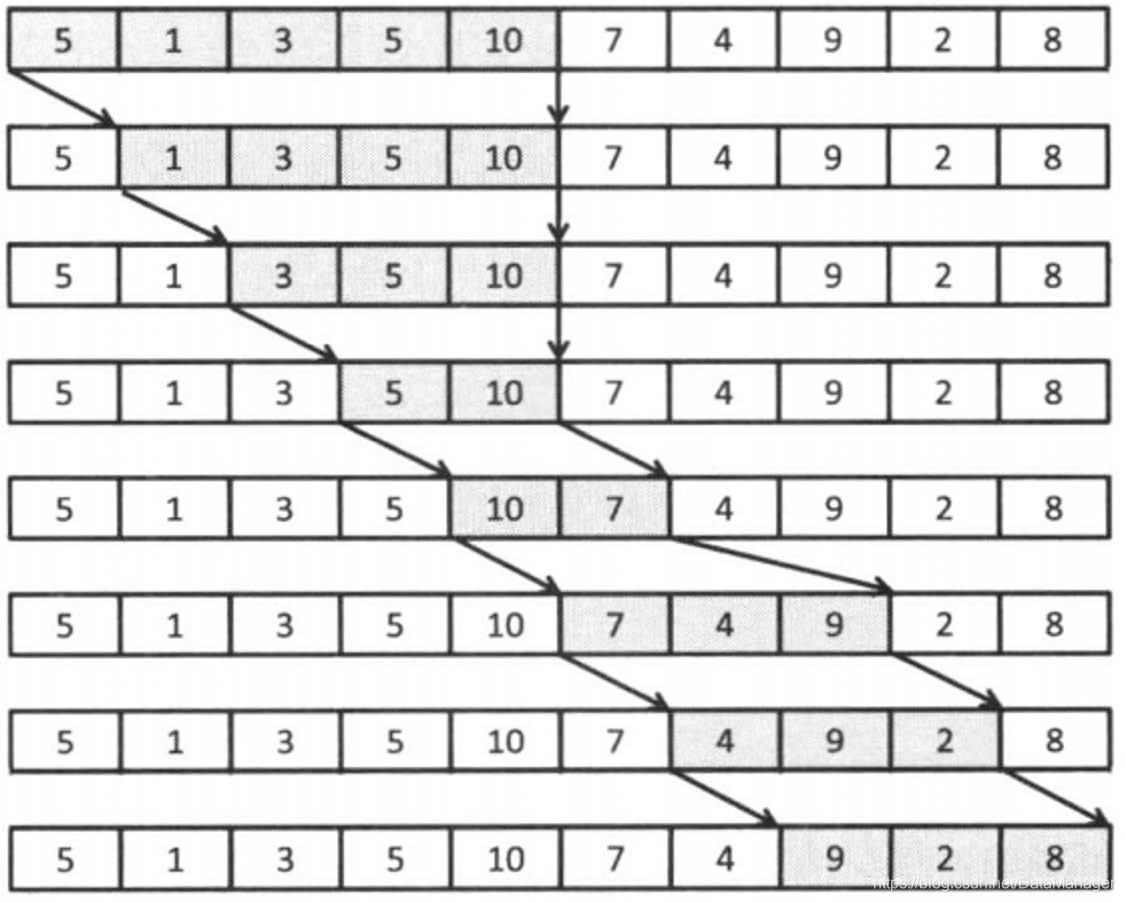
下面介绍前缀和的使用，和第二道例题差分思想非常类似，用一个新的SUMSUMSUM数组来代替原数组的数值关系，定义如下：
- SUM[i]=SUM[i−1]+a[i]SUM[i]=SUM[i-1]+a[i]SUM[i]=SUM[i−1]+a[i]
- SUM[l,r]=SUM[r]−SUM[l−1]SUM[l,r]=SUM[r]-SUM[l-1]SUM[l,r]=SUM[r]−SUM[l−1]
前缀和可以在O(1)O(1)O(1)复杂度下求出一个区域所有元素数值之和。
这样有了这两方面知识的铺垫，这道题基本就迎刃而解了，我们发现对于字符串问题而言，所要求得的答案在一个连续区间中，而且端点的移动方向是定向的，所以我们只需要从左到右利用双指针法（尺取法）进行遍历，找到满足条件的最短区间即可，尺取法代码如下：
void solve3()
{//tmp=sum[l,r] ,ans为最终答案
int n = strlen(c);
int ans = n+1,l = 1,r = 0;
while(r <= n)
{//假如r > n，所选区间已经不合法，因此退出循环
while(l <= r && satisfy(n,r,l))//换成满足的条件 )
{
ans = min(ans, r-l+1);
l++;
}
r++;
}
printf("%d",ans);
}
那么下面要解决的问题就是如何判断除了所选区间以外的元素满足条件呢？也就是要求替换以后所有元素的个数满足总个数的四分之一，我们采取这样的办法：
- 用sum1,sum2,sum3,sum4sum1, sum2, sum3, sum4sum1,sum2,sum3,sum4 分别记录不包含区间[L, R] 这一段时，字符Q,W,E,RQ,W,E,RQ,W,E,R的个数；
- 先通过替换使4类字符数量一致，再判断剩余空闲位置freefreefree是否为4的倍数；
- 若free≥0free ≥0free≥0且为4的倍数，则满足要求；否则不满足
判断是否满足条件的代码实现如下：
bool findM(vector<section>& v, int start, int right)
{//修剪区间并计数应选区间个数
bool judge = false;
int maxi = right;
int max_l = start;
right++;//这里注意要先付给maxi再++
for (vector<section>::iterator it = v.begin(); it != v.end(); it++)
{
if (it->left > right)break;//整个位于右侧则说明找完了，后面也不可能有了【排序造成的】
if (it->left > start&& it->left <= right)
{
if (it->right > maxi)
{
maxi = it->right;
max_l = it->left;
judge = true;
}
}
}
if (maxi != right-1)//这个地方也要注意
{
amt++;
tmp.left = max_l;
tmp.right = maxi;
}
right--;
return judge;
}
经过上述分析，下面是题目完整代码：
#include<iostream>
#include<math.h>
#include<string.h>
using namespace std;
const int N = 1e5 + 50;
char c[N];
int sum1,sum2,sum3,sum4;
int Q[N],W[N],E[N],R[N];
bool satisfy(int n,int r,int l)
{//判断
//sum1,sum2,sum3,sum4分别表示[1,n]去除[l,r]后，Q,W,E,R的个数
sum1 = Q[n]-(Q[r]-Q[l-1]);
sum2 = W[n]-(W[r]-W[l-1]);
sum3 = E[n]-(E[r]-E[l-1]);
sum4 = R[n]-(R[r]-R[l-1]);
int maxx = max(max(sum1,sum2),max(sum3,sum4));
int total = r-l+1;
//令sum1=sum2=sum3=sum4
total -= (maxx-sum1)+(maxx-sum2)+(maxx-sum3)+(maxx-sum4);
//判断剩下的可更改位置
if(total >= 0&& total%4 == 0)return true;
else return false;
}
void solve3()
{//tmp=sum[l,r] ,ans为最终答案
int n = strlen(c);
int ans = n+1,l = 1,r = 0;
while(r <= n)
{//假如r > n，所选区间已经不合法，因此退出循环
while(l <= r && satisfy(n,r,l))//换成满足的条件 )
{
ans = min(ans, r-l+1);
l++;
}
r++;
}
printf("%d",ans);
}
int main()
{
scanf("%s",c);
for(int i=1;i<=strlen(c);i++)
{
switch(c[i-1])
{
case 'Q':
Q[i]=Q[i-1]+1;
W[i]=W[i-1];
E[i]=E[i-1];
R[i]=R[i-1];
break;
case 'W':
W[i]=W[i-1]+1;
Q[i]=Q[i-1];
E[i]=E[i-1];
R[i]=R[i-1];
break;
case 'E':
E[i]=E[i-1]+1;
Q[i]=Q[i-1];
W[i]=W[i-1];
R[i]=R[i-1];
break;
default:
R[i]=R[i-1]+1;
Q[i]=Q[i-1];
E[i]=E[i-1];
W[i]=W[i-1];
break;
}
}
int n = strlen(c);
if(Q[n]==W[n] && W[n]==E[n] && E[n]==R[n])
{
printf("0");
return 0;
}
solve3();
return 0;
}
3.滑动窗口
题目描述
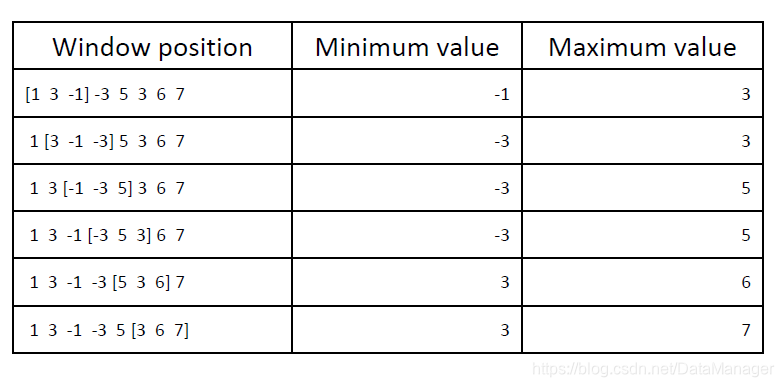
ZJM 有一个长度为 n 的数列和一个大小为 k 的窗口, 窗口可以在数列上来回移动. 现在 ZJM 想知道在窗口从左往右滑的时候，每次窗口内数的最大值和最小值分别是多少. 例如：
数列是 [1 3 -1 -3 5 3 6 7], 其中 k 等于 3.
- Input
输入有两行。第一行两个整数n和k分别表示数列的长度和滑动窗口的大小，1<=k<=n<=1000000。第二行有n个整数表示ZJM的数列。
- Output
输出有两行。第一行输出滑动窗口在从左到右的每个位置时，滑动窗口中的最小值。第二行是最大值。
题目分析
解决滑动窗口类的题目使用的数据结构为单调队列（FIFO），和第一题的单调栈类似，这里就不再赘述，仅把入队列和出队列的操作加以说明：
- 如果队列为空或者队尾元素小于入队元素，则入队。
- 否则，入队则会破坏队内元素的单调性，则需要将不满足条件的队尾元素全部出队后，将入队元素入队。
以数组[10,3,7,4,12][10,3,7,4,12][10,3,7,4,12]为例，从左到右依次入队的操作过程如下：
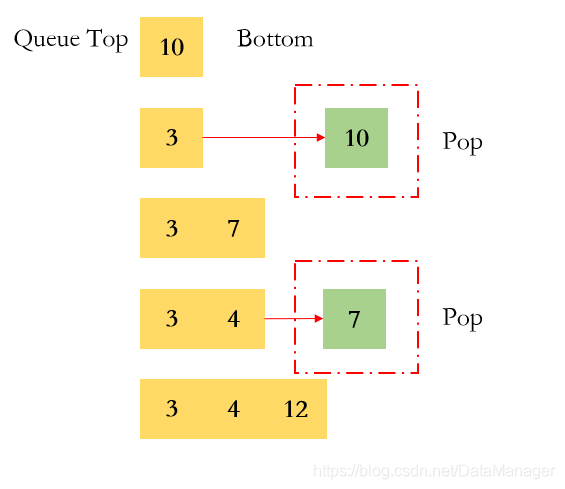
现在来分析具体题目，如果查找全局的最小值,可以使用单调栈（但是有些多余）现在要求查找窗口内的最小值,是一个局部的概念，那么维护一个单调递增队列是更好的选择,队列中的元素均属于当前窗口，当元素不属于当前窗口时,将队首元素弹出即可。
下面是利用单调队列查找局部最小值和最大值的实现代码：
void find_min()
{
int l=1,r=0;
for(int i = 1;i <= n;i++)
{//q[r]为队首元素在a中索引
while(r >= l && a[q[r]]>=a[i])
{//保证队列不为空
r--;
}
q[++r] = i;
if(q[r] - q[l] + 1 > k) l++;
if(i>=k && i!=n) printf("%d ",a[q[l]]);
else if(i==n) printf("%d",a[q[l]]);
}
printf("\n");
}
void find_max()
{
int l=1,r=0;
for(int i = 1;i <= n;i++)
{//q[r]为队首元素在a中索引
while(r >= l && a[q[r]] <= a[i])
{//保证队列不为空
r--;
}
q[++r] = i;
if(q[r] - q[l] + 1 > k) l++;
if(i>=k && i!=n) printf("%d ",a[q[l]]);
else if(i==n) printf("%d",a[q[l]]);
}
}
经过上述分析，下面是题目完整代码：
#include<iostream>
#include<math.h>
using namespace std;
const int N = 1e6 + 100;
int a[N],R[N],L[N],q[N];
int n,k;
void find_min()
{
int l=1,r=0;
for(int i = 1;i <= n;i++)
{//q[r]为队首元素在a中索引
while(r >= l && a[q[r]]>=a[i])
{//保证队列不为空
r--;
}
q[++r] = i;
if(q[r] - q[l] + 1 > k) l++;
if(i>=k && i!=n) printf("%d ",a[q[l]]);
else if(i==n) printf("%d",a[q[l]]);
}
printf("\n");
}
void find_max()
{
int l=1,r=0;
for(int i = 1;i <= n;i++)
{//q[r]为队首元素在a中索引
while(r >= l && a[q[r]] <= a[i])
{//保证队列不为空
r--;
}
q[++r] = i;
if(q[r] - q[l] + 1 > k) l++;
if(i>=k && i!=n) printf("%d ",a[q[l]]);
else if(i==n) printf("%d",a[q[l]]);
}
}
int main()
{
scanf("%d%d",&n,&k);
getchar();
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
find_min();
find_max();
return 0;
}
扫一扫
1435
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
