程序设计思维与实践 Week3 Blog

原创 于 2020-04-02 22:48:34 发布 · 173 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构

本文深入解析选数问题中的可行性剪枝技巧，区间选点及区间覆盖问题的贪心算法应用。通过实例讲解，提供代码实现，帮助读者掌握算法核心思想。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

一、大纲

本周作业与实验题目如下：

  • 选数问题（可行性剪枝）
  • 区间选点（贪心算法）
  • 区间覆盖（贪心算法）

二、逐个击破

1.选数问题

题目描述

  Given n positive numbers, ZJM can select exactly K of them that sums to S. Now ZJM wonders how many ways to get it!

  1. Input

  The first line, an integer T<=100, indicates the number of test cases. For each case, there are two lines. The first line, three integers indicate n, K and S. The second line, n integers indicate the positive numbers.

  1. Output

  For each case, an integer indicate the answer in a independent line.

题目分析

  该题是一个典型的子集枚举类问题，子集枚举通过递归实现，其中int型链表res用于存储在递归过程中当前子集的情况，sum为所要求得的总和，在递归过程中让sum不断减去选择的数，如果最后恰好为0则说明满足条件。然而显然把所有情况全部枚举的时间复杂度太高，已经达到了 O(K∗2n)\ O(K*2^{n}) O(K∗2n), 因此应该考虑有哪些情况下可以不用继续枚举，这也是可行性剪枝来优化算法的主要思想，就本题而言，在两个条件下可以施行剪枝：

  • 选择数的个数超过了 K
  • 当前数的总和已经超过了S

  子集枚举函数的代码如下：

void select(int n, int sum, list<int> &res)
{
		if(res.size()==K && sum==0)
		{
			totle++;
			return;
		}
	if(n >= N || res.size() > K || sum < 0) return;
	select(n+1,sum,res);
	res.push_back(number[n]);
	select(n+1,sum-number[n],res);
	res.pop_back();
}

  这里需要特别注意的一个点是由于题目要求多组数据的输入输出，而上面在编程实现时开辟的全局数据结构需要清空操作clear()。
  综上所述本题目的实现代码如下：

#include<iostream>
#include<list>
#include<vector>
using namespace std;

int T;
int N,K,S;
vector<int> number;
int totle=0;

void select(int n, int sum, list<int> &res)
{
		if(res.size()==K && sum==0)
		{
			totle++;
			return;
		}
	if(n >= N || res.size() > K || sum < 0) return;
	select(n+1,sum,res);
	res.push_back(number[n]);
	select(n+1,sum-number[n],res);
	res.pop_back();
}


int main()
{
	scanf("%d",&T);
	for(int i=0;i<T;i++)
	{
		list<int> res;
		scanf("%d%d%d",&N,&K,&S); 
		for(int j=0;j<N;j++)
		{
			int tmp;
			scanf("%d",&tmp);
			number.push_back(tmp);
		}
		select(0,S,res);
		if(i==T-1) printf("%d",totle);
		else printf("%d\n",totle);
		number.clear();
		totle=0;
	 } 
 }

2.区间选点问题

题目描述

  数轴上有 n 个闭区间 [a_i, b_i]。取尽量少的点，使得每个区间内都至少有一个点（不同区间内含的点可以是同一个）

  1. Input

第一行1个整数N（N<=100）
第2~N+1行，每行两个整数a,b（a,b<=100）
Example:
  3
  1 3
  2 5
  4 6

  1. Output

一个整数，代表选点的数目
Example:
  2

题目分析

  由题意知，要求选尽可能少的点能够落在所有区间中，可以尝试使用贪心算法来解决，贪心算法的基本思想是对局部情况做出局部最优的策略从而最终得到全局最优解，但是贪心准则的选择各式各样，哪种贪心准则才能得到全局最优解是我们最关注的问题。
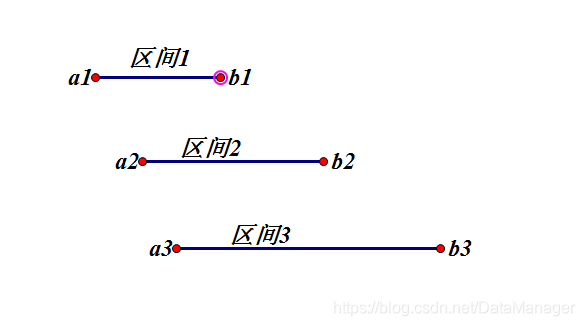
在这里插入图片描述

  就这道题而言，我们选取的贪心准则为：在排序好的区间上依次判断当前区间的右端点是否落在下一个最邻近区间中，如果不覆盖就需要添加一个点，否则不需要添加，继续进行下一个区间判断。而排序方法使用多关键字排序，第一关键字为区间的右端点，第二关键字为区间的左端点。

  证明：（在已经排好序情况下）
   1.首先，从第一个区间 S1S_1S1​ 开始，为了能够覆盖第一个区间，我们必须选取第一个区间中的点，那么选择哪个位置呢？不难发现，右端点b1b_1b1​是在能保证覆盖当前区间的情况下有最大可能性覆盖其他区间的点，所以我们在单个区间中选点一定选择右端点，然后往后遍历区间，直至第iii个区间SiS_iSi​的左端点ai>b1a_i>b_1ai​>b1​
   2.然后，再在SiS_iSi​区间选取点，我们发现这又回归到了第一个区间面临的同样的问题，这样往后重复1的步骤直至遍历全部结束，选择其他位置都会让解更差所以最后可以获得最优解。

Tips:
   注意这里也间接解释了为什么多关键字排序要按照上述方式进行，因为我们比较的是区间右端点能否覆盖遍历过程中区间的左端点，所以要保证先按右端点排序，再按照左端点排序。

  section区间结构体的定义和操作符重载（多关键字排序）代码如下：

struct section
{
	int left;
	int right;
	bool operator<(section &s)const
	{
		if(right!=s.right)return right<s.right;
		else return left<s.left;
		}	
};

  贪心准则的实现如下：

for(vector<section>::iterator it=store.begin();it!=store.end()-1;it++)
	{//贪心准则为每次判断区间右端点是否覆盖下一个最邻近区间 
		if(flag<(it+1)->left)
		{
			amt++;
			flag=(it+1)->right;
			continue;
		}
		
	}

  区间选点问题的全部实现代码如下：

#include<iostream>
#include<map>
#include<vector>
#include<algorithm>
using namespace std;

struct section
{
	int left;
	int right;
	bool operator<(section &s)const
	{
		if(right!=s.right)return right<s.right;
		else return left<s.left;
		}	
};

vector<section> store;//用于存储所有区间 

int main()
{
	int cnt;
	scanf("%d",&cnt);
	for(int i=0;i<cnt;i++)
	{
		section current;
		scanf("%d%d",&current.left,&current.right);
		store.push_back(current);
	}
	sort(store.begin(),store.end());
	int amt=1;
	int flag=store[0].right;
	for(vector<section>::iterator it=store.begin();it!=store.end()-1;it++)
	{//贪心准则为每次判断区间右端点是否覆盖下一个最邻近区间 
		if(flag<(it+1)->left)
		{
			amt++;
			flag=(it+1)->right;
			continue;
		}
		
	}
	printf("%d",amt);
	return 0;
 }

Tips:
   在vector数组迭代器遍历过程中要注意it的终止位置为end()-1,因为下面的判断需要用到it+1区间的左端点，否则会出现数组越界的问题。

3.区间覆盖问题

题目描述

  数轴上有 n (1<=n<=25000)个闭区间 [ai, bi]，选择尽量少的区间覆盖一条指定线段 [1, t]（ 1<=t<=1,000,000）。
   覆盖整点，即(1,2)+(3,4)可以覆盖(1,4)。
   不可能办到输出-1

  • Input

   第一行：N和T
   第二行至N+1行: 每一行一个闭区间。

  • Output

   选择的区间的数目，不可能办到输出 -1

题目分析

   这道题目和区间选点问题比较类似，而且发现贪心准则的实现基本都是基于对于某种参数Γ\GammaΓ的排序，例如
   背包问题中：Γ=ValueWeight\Gamma=\frac{Value}{Weight}Γ=WeightValue​
   区间选点问题：Γ1=Pright,Γ2=Pleft\Gamma_1=P_{right},\Gamma_2=P_{left}Γ1​=Pright​,Γ2​=Pleft​
   区间覆盖问题：Γ1=Pleft,Γ2=Pright\Gamma_1=P_{left},\Gamma_2=P_{right}Γ1​=Pleft​,Γ2​=Pright​
   按照区间左端点升序排序，右端点降序排序，贪心准则为选择起点为1的最长区间[1,bi][1,b_i][1,bi​]，然后bib_ibi​作为新起点寻找延申最长区间直至结束。选择该种排序方法的原因是用左端点去找最长的右端点所以采用该种多关键字排序方式。

   但是在具体实现过程中有一些细节处理可以避免很多麻烦，比如在输入区间的时候由于题目要求覆盖区间[1,t][1,t][1,t],所以以下两种情况可以不加入vector中：

  • 区间的右端点小于1
  • 区间的左端点大于t

   如果对于区间[a,b][a,b][a,b],a<1a<1a<1而且b>1b>1b>1,那么可以将该区间裁剪为[1,b][1,b][1,b]以后再加入vector，因为1左侧的部分对于我们的答案没有影响，而且在后续中我们还需要逐个对区间进行修剪，所以为了排序的便利直接在输入时进行这种预处理可以减少部分后续操作。例如： 区间[−3,5][-3,5][−3,5]和[−1,6][-1,6][−1,6]分别裁剪为[1,5][1,5][1,5]和[1,6][1,6][1,6] 再压入队列中，如下图所示
在这里插入图片描述
   该部分代码如下：

	int N, T;
	scanf("%d%d", &N, &T);
	for (int i = 0; i < N; i++)
	{
		section current;
		scanf("%d%d", &current.left, &current.right);
		if (current.left < 1) current.left = 1;
		if (current.right >= 1 && current.left <= T)
			store.push_back(current);
	}

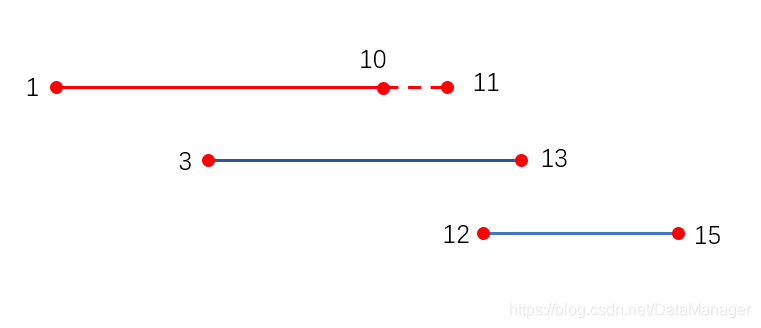
  然后就是一些贪心算法的具体实现问题，还是有不少细节的，例如覆盖整点即可的问题，所以我们区间比较的时候（红色线段区间）右端点可以暂时加一（虚线部分），然后在函数结束的时候要注意恢复原本右端点，否则区间就在慢慢变长，当出现无法覆盖的区间的时候有如下两种情况：
（红色线段为当前选择好的区间，发现无法覆盖下面两条蓝色线段，对于区间[3,13][3,13][3,13]则需要添加作为新的选择区间，cnt+1，然而如果出现区间[12,15][12,15][12,15]的情况，则说明出现了断点，不可能全部覆盖，返回false即可）
在这里插入图片描述
  代码实现如下：

bool findM(vector<section>& v, int start, int right)
{//修剪区间并计数应选区间个数 
	bool judge = false;
	
	int maxi = right;
	int max_l = start;
	right++;//这里注意要先付给maxi再++
	for (vector<section>::iterator it = v.begin(); it != v.end(); it++)
	{
		if (it->left > right)break;//整个位于右侧则说明找完了，后面也不可能有了【排序造成的】
 
		if (it->left > start&& it->left <= right)
		{
			if (it->right > maxi)
			{
				maxi = it->right;
				max_l = it->left;
				judge = true;
			}
		}
	}
	if (maxi != right-1)//这个地方也要注意
	{
		amt++;
		tmp.left = max_l;
		tmp.right = maxi;
	}
	right--;
	return judge;
}

  经过上述分析，下面是题目完整代码：

#include<iostream>
#include<map>
#include<vector>
#include<algorithm>
using namespace std;

struct section
{
	int left;
	int right;
	bool operator<(section& s)const
	{//对左端点进行升序排序，右端点降序 
		if (left != s.left) return left < s.left;
		else return right > s.right;
	}
};

int amt = 1;
section tmp;

bool findM(vector<section>& v, int start, int right)
{//修剪区间并计数应选区间个数 
	bool judge = false;
	
	int maxi = right;
	int max_l = start;
	right++;//这里注意要先付给maxi再++
	for (vector<section>::iterator it = v.begin(); it != v.end(); it++)
	{
		if (it->left > right)break;//整个位于右侧则说明找完了，后面也不可能有了【排序造成的】

		if (it->left > start&& it->left <= right)
		{
			if (it->right > maxi)
			{
				maxi = it->right;
				max_l = it->left;
				judge = true;
			}
		}
	}
	if (maxi != right-1)//这个地方也要注意
	{
		amt++;
		tmp.left = max_l;
		tmp.right = maxi;
	}
	right--;
	return judge;
}

vector<section> store;//用于存储所有区间 

int main()
{
	int N, T;
	scanf("%d%d", &N, &T);
	for (int i = 0; i < N; i++)
	{
		section current;
		scanf("%d%d", &current.left, &current.right);
		if (current.left < 1) current.left = 1;
		if (current.right >= 1 && current.left <= T)
			store.push_back(current);
	}
	if (store.empty())
	{
		printf("-1");
		return 0;
	}
	sort(store.begin(), store.end());


	//首先找出可能出现无法覆盖的情况
	bool flag = false;
	for (vector<section>::iterator it = store.begin(); it != store.end(); it++)
	{//寻找是否存在>=T的点以及<1的点，否则输出-1
		if (it->right >= T)flag = true;
	}
	if (store[0].left > 1 || flag == false)
	{
		printf("-1");
		return 0;
	}

	tmp.right = store[0].right;//因为第一个一定是最大的
	tmp.left = store[0].left;
	while (tmp.right < T)
	{
		if (!findM(store, tmp.left, tmp.right))
		{
			printf("-1");
			return 0;
		}
	}
	printf("%d", amt);
	return 0;
}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值