SLAM——之GTSAM函数库

最新推荐文章于 2025-11-15 18:04:11 发布

原创最新推荐文章于 2025-11-15 18:04:11 发布 · 1.7k 阅读

6 ·

CC 4.0 BY-SA版权

文章标签：

#算法

SLAM 专栏收录该内容

82 篇文章

订阅专栏

本文介绍了GTSAM库中如何利用因子图表示隐马尔可夫模型，并详细展示了使用BetweenFactor和PriorFactor构建高斯因子图的过程。重点讲解了信赖区域法（列文伯格方法）在优化估计中的应用，通过实际代码演示了如何使用LevenbergMarquardtOptimizer进行最小二乘求解。最后，展示了如何计算变量的边缘概率和信息量。

Factor Graphs and GTSAM

1. 因子图表达

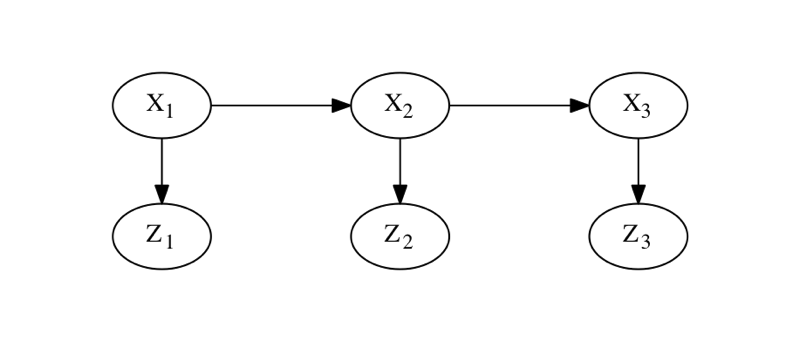
在这里插入图片描述

上图为一个HMM（隐马尔可夫链）模型
其因子图为（用来极大化最大后验误差）：

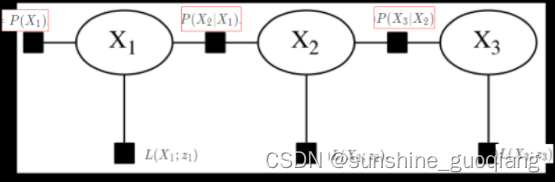
在这里插入图片描述
以一个马尔可夫链为例

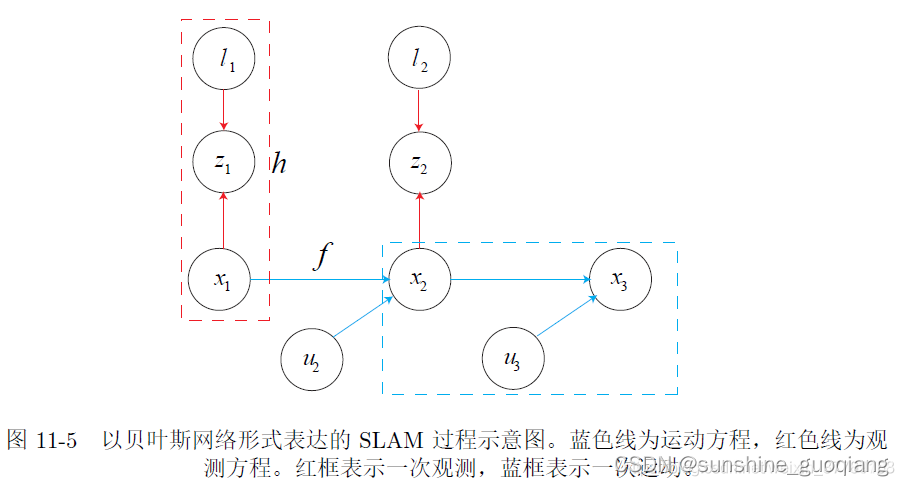
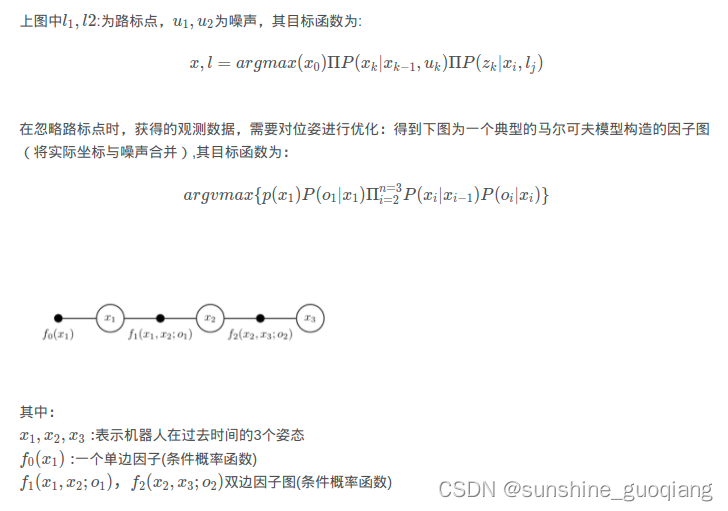
代码:

//BetweenFactor 包含描述两个因子之间相关操作类
//              和初始状态概率矩阵
#include <gtsam/slam/BetweenFactor.h>
//误差
#include <gtsam/slam/PriorFactor.h> 
//非线性
#include <gtsam/nonlinear/NonlinearFactorGraph.h>
//列文伯格求解方程组
#include <gtsam/nonlinear/LevenbergMarquardtOptimizer.h>
//Pose2 类库 把3d点用作(x,y,theta)表示
#include <gtsam/geometry/Pose2.h>
#include <iostream>
//计算边缘分布
#include <gtsam/nonlinear/Marginals.h>

//指定列文伯格迭代的初始值
#include <gtsam/nonlinear/Values.h>
#include <gtsam/base/Vector.h>
#include <CppUnitLite/TestHarness.h>// 单元测试库
#include <boost/shared_ptr.hpp>
#include <boost/assign/std/list.hpp>
using namespace std;
using namespace gtsam;
int main(int argc, const char** argv) {
    NonlinearFactorGraph graph;//高斯因子图

    //3d点
    Pose2 priorMean(0,0,0);//先验值 x,y,theta
    //Pose2(Point2,Rot2):位置姿态
    //Rot2(cos(theta),sin(theta)):夹角的余弦值和正弦值
    
    //添加噪声，替他还有gussian,Robust、Unit 噪声
    noiseModel::Diagonal::shared_ptr priorNoise=noiseModel::Diagonal::Sigmas(Vector3(0.3,0.3,0.1));
    //Eigen::Vector3
    //sigma函数:1/(1+e^(-z))
    noiseModel::Diagonal::shared_ptr odometryNoise = noiseModel::Diagonal::Sigmas(Vector3(0.2, 0.2, 0.1));
    //在因子图中添加因子（//初始化）
    //graph.add(PriorFactor<Pose2>(1,priorMean,odometryNoise));//添加单个
    graph.emplace_shared<PriorFactor<Pose2> >(1,priorMean,priorNoise);//可以添加多个
    //1 因子图顺序 priorMean 数据 odometryNoise 噪声
    Pose2 odometry(2.0,0,0);
    graph.emplace_shared<BetweenFactor<Pose2> >(1,2,odometry,odometryNoise);
    //t-1:1,t:2 odometry数据，odometryNoise噪声
    
    graph.emplace_shared<BetweenFactor<Pose2> >(2,3,odometry,odometryNoise);

    graph.print("\nFactor Graph:\n");//等价与print

    Values initial;
    //初始化观测矩阵
    initial.insert(1, Pose2(0.5, 0.0, 0.2));//插入观测数据
    initial.insert(2, Pose2(2.3, 0.1, -0.2));
    initial.insert(3, Pose2(4.1, 0.1, 0.1));
    initial.print("\nInitial Estimate:\n"); // print

    //使用列文伯格迭代求解最小二乘:min(z-gussan（x+w)-gussan(y+v)+gussan(z+e))
    Values result=LevenbergMarquardtOptimizer(graph,initial).optimize();//经过三次迭代后的预测值
    result.print("Final Result:\n");

    
    //cout<<"date"<<result.find(1)<<endl;
    //cout<<<"result:"<<<<endl;
    cout.precision(2);//精度 streamsize设为2,小数点后两为
    

    
    //计算非线性因子图中变量的高斯边缘概率
    Marginals marginals(graph, result);
    
    cout << "x1 covariance:\n" << marginals.marginalCovariance(1) << endl;   
    cout << "x2 covariance:\n" << marginals.marginalCovariance(2) << endl;
    cout << "x3 covariance:\n" << marginals.marginalCovariance(3) << endl;
    cout << "x1 marginalInformation:\n" << marginals.marginalInformation(1) << endl;
    cout << "x2 marginalInformation:\n" << marginals.marginalInformation(2) << endl;
    cout << "x3 marginalInformation:\n" << marginals.marginalInformation(3) << endl;
    
    //查询优化结果
    for (const gtsam::Values::ConstKeyValuePair& key_value: result )
    {   
        cout<<"key "<<key_value.key<<endl;
        Pose2 pose = key_value.value.cast<gtsam::Pose2>();//类型转换
        cout<<"data:"<<pose.matrix()<<endl;
    }
    //遍历
    for ( gtsam::NonlinearFactor::shared_ptr factor: graph )//遍历因子图节点
    {
         gtsam::BetweenFactor<gtsam::Pose2>::shared_ptr f = dynamic_pointer_cast<gtsam::BetweenFactor<gtsam::Pose2>>( factor );//提取边
         if (f){
                 gtsam::SharedNoiseModel model = f->noiseModel();//提取噪声模型
                 gtsam::noiseModel::Diagonal::shared_ptr DiagModel = dynamic_pointer_cast<gtsam::noiseModel::Diagonal>( model );//从噪声模型提取高斯模型
                 if ( DiagModel )
                {       
                    gtsam::Matrix info;   
                    gtsam::Vector DiagModel_sigma=DiagModel->sigmas();
                    cout<<"DiagModel_sigma:"<<DiagModel_sigma<<endl;//输出误差
                    Pose2 pose=f->measured();
                    cout<<"data:"<<pose.matrix()<<endl;//显示测量
                }
         }
    }
    return 0;
}