这篇博客主要介绍桶排序、计数排序和基数排序的工作原理及流程,并介绍其中的差别。
若是不想听博主的 废话 大段文字,可以跳到文末。
桶排序(Bucket sort)
桶排序的工作的原理是将数组分到
k
k
k 的桶里。
其工作流程为:
- 扫描一遍序列求出最大值 m a x V maxV maxV 和最小值 m i n V minV minV ,设桶的个数为 k k k ,则把区间 [ m i n V , m a x V ] [minV, maxV] [minV,maxV] 均匀划分成 k k k 个区间,每个区间就是一个桶。将序列中的元素分配到各自的桶。
- 对每个桶内的元素进行排序。可以选择任意一种排序算法。
- 将各个桶中的元素合并成一个大的有序序列。
- 举例来说,若是对每个桶使用快排(假设数据是均匀分布的,则每个桶的元素平均个数为 n/k),则单次排序复杂度为
O
(
n
/
k
⋅
l
o
g
2
n
/
k
)
O(n/k \cdot log_2n/k)
O(n/k⋅log2n/k),则总复杂度为
O
(
n
+
k
⋅
n
/
k
⋅
l
o
g
2
n
/
k
)
=
O
(
n
+
n
l
o
g
n
−
n
l
o
g
k
)
O(n + k \cdot n/k\cdot log_2n/k) = O(n+nlogn-nlogk)
O(n+k⋅n/k⋅log2n/k)=O(n+nlogn−nlogk)
总的来说,桶排序是将数据划分为 k k k 个桶,分别进行排序,其时间复杂度随着桶的数量( k k k)的增加而减少,趋向 O ( n ) O(n) O(n) ,但同时空间复杂度也会增加至 m a x V − m i n V maxV - minV maxV−minV
性质
- 平均时间复杂度:O(n + k)
- 最佳时间复杂度:O(n + k)
- 最差时间复杂度:O(n ^ 2)
- 空间复杂度:O(k)
- 稳定性:稳定
计数排序
简单来说,计数排序可以理解为一种特殊的桶排,即
k
=
n
k = n
k=n 的情况。
其工作流程为:
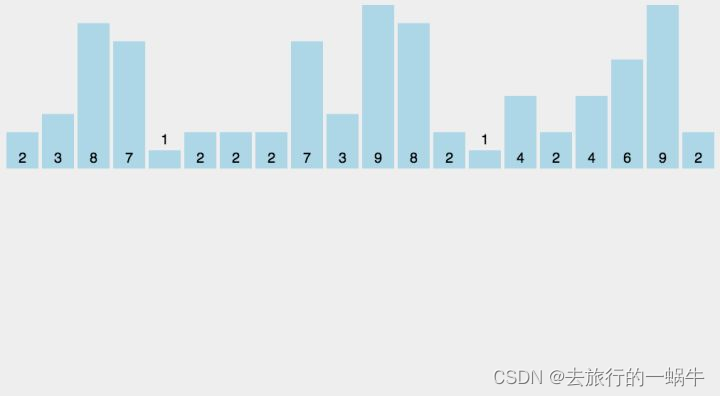
- 求出最大值 m a x V maxV maxV 和最小值 m i n V minV minV,开出 m a x V − m i n V maxV - minV maxV−minV 大的空间,然后将元素一次放进桶中(其实就是一个数组,记录大小等于其下标的元素的个数)
- 依次按顺序取出元素
性质
k k k 为其值域范围
- 平均时间复杂度:O(n + k)
- 最佳时间复杂度:O(n + k)
- 最差时间复杂度:O(n + k)
- 空间复杂度:O(k)
- 稳定性:稳定
基数排序
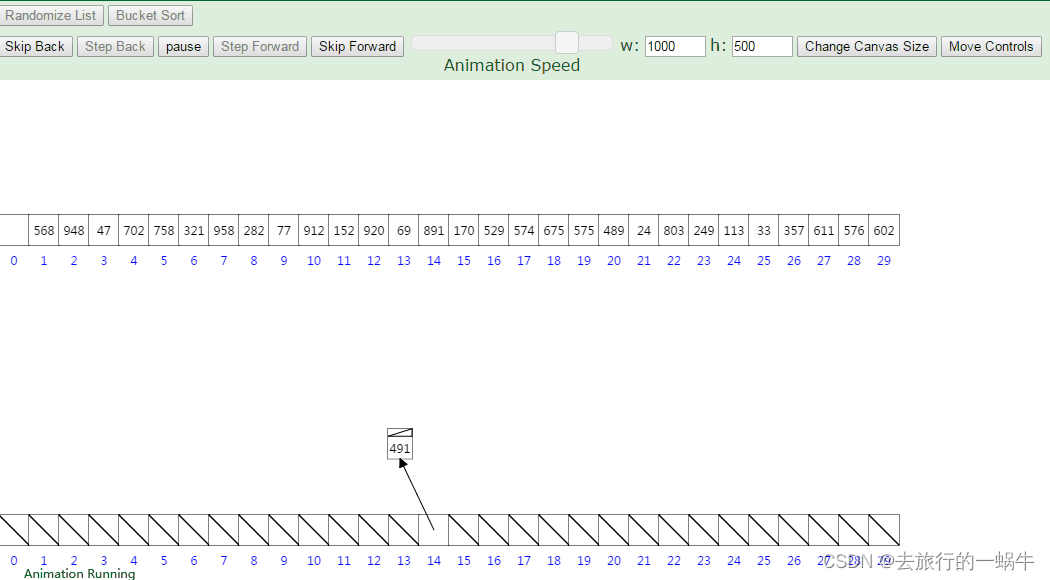
其核心思想为按位进行比较,从而达到排序的效果,附动图一张:

若是想详细了解可以看这个:【初赛】基数排序
性质
- 平均时间复杂度:O(n * k)
- 空间复杂度:O(n + k)
- 稳定性:稳定
总结
- 计数排序为特殊的桶排,其桶的个数 k = m a x V − m i n V k = maxV - minV k=maxV−minV
- 基数排序是按位进行分割比较,进行计数排序或桶排(其本质便是按位进行多次桶排)
- 在复杂度和适用范围上,他们也不尽相同:
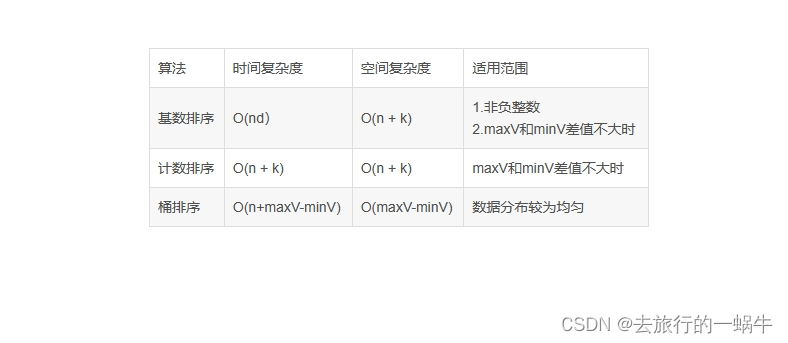




 本文详细介绍了桶排序、计数排序和基数排序的工作流程、时间复杂度、空间复杂度以及稳定性。桶排序通过均匀划分桶进行排序,计数排序是特殊桶排序(k=n),基数排序按位比较。
本文详细介绍了桶排序、计数排序和基数排序的工作流程、时间复杂度、空间复杂度以及稳定性。桶排序通过均匀划分桶进行排序,计数排序是特殊桶排序(k=n),基数排序按位比较。
















 1334
1334

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








