本次模拟测试包含三道题目，分别涉及高级数据结构、树的遍历与查询、以及复杂数学运算。第一题使用了预处理和哈希技巧解决大规模组合计算；第二题通过树的构建与LCA算法解决弦的匹配问题；第三题则深入探讨了树状结构的查询优化。本文详细介绍了每题的解析思路与代码实现。
191106-模拟测试13
T1
题目描述
解析
完全不会
直接放篇题解
题解
#ifndef K_ON
#define K_ON
#endif
#include <bits/stdc++.h>
using namespace std;
#define DEBUG(...) fprintf(stderr, __VA_ARGS__)
#define mp make_pair
#define fst first
#define snd second
#define SZ(u) ((int) (u).size())
#define ALL(u) (u).begin(), (u).end()
inline void proc_status()
{
ifstream t("/proc/self/status");
cerr << string(istreambuf_iterator<char>(t), istreambuf_iterator<char>()) << endl;
}
template<typename T> inline bool chkmin(T &a, const T &b) { return a > b ? a = b, 1 : 0; }
template<typename T> inline bool chkmax(T &a, const T &b) { return a < b ? a = b, 1 : 0; }
template<typename T> inline T read()
{
register T sum(0), fg(1);
register char ch(getchar());
for(; !isdigit(ch); ch = getchar()) if(ch == '-') fg = -1;
for(; isdigit(ch); ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ '0');
return sum * fg;
}
typedef long long LL;
typedef pair<int, int> pii;
const int MOD = 9990017;
LL n, m, B;
inline void input()
{
n = read<LL>(), m = read<LL>(), B = read<LL>();
}
inline int fpm(int x, int y)
{
int res = 1;
for(; y; y >>= 1, x = (LL) x * x % MOD) if(y & 1) res = (LL) res * x % MOD;
return res;
}
const int MAXN = (int) pow(1e10, 2.0 / 3);
int fac[MOD], ifac[MOD];
int pre_f0[MAXN + 5];
inline int C0(LL N, LL M) { return N < M ? 0 : (LL) fac[N] * ifac[N - M] % MOD * ifac[M] % MOD; }
inline int C(LL N, LL M) { return N < M ? 0 : (LL) C0(N % MOD, M % MOD) * (N >= MOD ? C(N / MOD, M / MOD) : 1) % MOD; }
inline void MATH_init()
{
fac[0] = 1;
for(int i = 1; i < MOD; ++i) fac[i] = (LL) fac[i - 1] * i % MOD;
ifac[MOD - 1] = fpm(fac[MOD - 1], MOD - 2);
for(int i = MOD - 2; i >= 0; --i) ifac[i] = (LL) ifac[i + 1] * (i + 1) % MOD;
for(int i = 1; i <= MAXN; ++i) pre_f0[i] = C(i, B);
for(int i = 1; i <= MAXN; ++i)
for(int j = i * 2; j <= MAXN; j += i)
(pre_f0[j] -= pre_f0[i]) %= MOD;
for(int i = 1; i <= MAXN; ++i) (pre_f0[i] += pre_f0[i - 1]) %= MOD;
}
unordered_map<LL, int> pre_f;
inline int S(LL N)
{
if(N <= MAXN) return pre_f0[N];
if(pre_f.count(N)) return pre_f[N];
int res = C(N + 1, B + 1);
for(LL i = 2, j; i <= N; i = j + 1)
{
j = N / (N / i);
res -= (LL) S(N / i) * (j - i + 1) % MOD;
res = res < 0 ? res + MOD : res;
}
return pre_f[N] = res;
}
inline void solve()
{
MATH_init();
int ans = 0;
for(LL i = 1, j; i <= min(n, m); i = j + 1)
{
j = min(n / (n / i), m / (m / i));
(ans += (LL) (S(j) - S(i - 1)) % MOD * (n / i) % MOD * (m / i) % MOD) %= MOD;
}
printf("%d\n", (ans + MOD) % MOD);
}
int main()
{
freopen("fuwafuwatime.in", "r", stdin);
freopen("fuwafuwatime.out", "w", stdout);
input();
solve();
return 0;
}
T2
题目描述
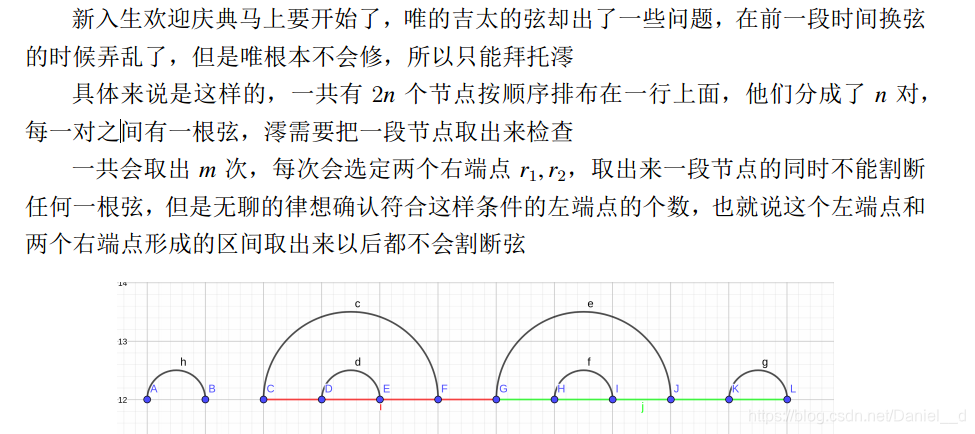
解析
1，std做法
建立一棵树，然后求lca即可
2，玄学做法
给每个弦的左右端点哈希一个值，然后将问题离线下来，然后计算前缀异或和，当前缀异或和相同时，那么便是一个合法区间，开个桶来记录就好了。（可能会冲突）
题解（std）
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#define LL long long
using namespace std;
const LL maxn=2e6+10;
LL read(){
LL x=0,f=1;char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
LL fir[maxn],nxt[maxn<<1],to[maxn],pos,tot=1,root[maxn];
LL n,m,match[maxn],l[maxn],r[maxn],fa[maxn][22],dep[maxn];
void add(LL x,LL y){nxt[++tot]=fir[x];fir[x]=tot;to[tot]=y;}
void dfs(LL x,LL rt){
root[x]=rt;
for(LL i=0;i<=20;i++) fa[x][i+1]=fa[fa[x][i]][i];
for(LL i=fir[x];i;i=nxt[i]){
LL y=to[i];if(y==fa[x][0]) continue;
fa[y][0]=x;dep[y]=dep[x]+1;
dfs(y,rt);
}
}
void build(){
vector<LL> sta;
for(LL i=1;i<=2*n;i++){
l[i]=min(i,match[i]);
r[i]=max(i,match[i]);
while(!sta.empty() && sta.back()>=l[i]){
pos=sta.back();sta.pop_back();
l[i]=min(l[i],l[pos]);
r[i]=max(r[i],r[pos]);
}
sta.push_back(i);
}
for(LL i=0;i<=2*n;++i) root[i]=-1;
for(LL i=1;i<=2*n;i++)
if(i==r[i]){
add(l[i]-1,i);
}
for(LL i=0;i<=2*n;i++) if(fir[i] && root[i]==-1){
dfs(i,i);
}
}
LL query(LL x,LL y){
if(root[x]!=root[y]) return 0;
if(dep[x]<dep[y]) swap(x,y);
for(LL i=21;i>=0;i--){
if(dep[fa[x][i]]>=dep[y]) x=fa[x][i];
}
if(x==y) return dep[x];
for(LL i=21;i>=0;i--){
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];y=fa[y][i];
}
}
return dep[fa[x][0]];
}
int main(){
//freopen("hotchkiss1.in","r",stdin);
//freopen("hotchkiss.out","w",stdout);
n=read();m=read();
for(LL i=1;i<=2*n;i++) match[i]=read();
build();
for(LL i=1,r1,r2;i<=m;i++){
r1=read();r2=read();
if(r1==0 || r2==0){
printf("0\n");continue;
}
if(r1==r2){
printf("%lld\n",dep[r1]);
}
else{
printf("%lld\n",query(r1,r2));
}
}
}
题解2 玄学做法
#include<bits/stdc++.h>
#define cs const
using namespace std;
typedef long long ll;
int read(){
int cnt = 0, f = 1; char ch = 0;
while(!isdigit(ch)){ ch = getchar(); if(ch == '-') f = -1; }
while(isdigit(ch)) cnt = cnt*10 + (ch-'0'), ch = getchar();
return cnt * f;
}
cs int N = 2e6 + 5;
int n, m, l[N], r[N], ct;
bool isr[N];
typedef long long ll;
ll d[N], b[N]; int sz;
ll rnd(){ return (rand() | ((ll)rand() << 15)) * (rand() | ((ll)rand() << 15)); }
vector<int> v[N];
#define pb push_back
int ans[N], bin[N];
int main(){
srand(time(0));
freopen("hotchkiss.in","r",stdin);
freopen("hotchkiss.out","w",stdout);
n = read(), m = read();
for(int i = 1; i <= (n << 1); i++){
int x = read();
if(x > i){ l[++ct] = i; r[ct] = x; isr[x] = true; }
}
for(int i = 1; i <= ct; i++){
d[l[i]] = d[r[i]] = rnd();
}
for(int i = 1; i <= (n << 1); i++){
d[i] ^= d[i-1];
}
if(n <= 2e3){
for(int i = 1; i <= m; i++){
int r1 = read(), r2 = read();
if(r1 > r2) swap(r1, r2);
if(!r1){ puts("0"); continue; }
if(!isr[r1] || !isr[r2]){ puts("0"); continue; }
if(d[r1] != d[r2]){ puts("0"); continue; }
int ans = 0;
for(int l = 1; l < r1; l++) if(!isr[l] && d[l - 1] == d[r1]) ++ans;
cout << ans << '\n';
}
}
else{
for(int i = 1; i <= (n << 1); i++) b[++sz] = d[i]; b[++sz] = d[0];
sort(b + 1, b + sz + 1); sz = unique(b + 1, b + sz + 1) - (b + 1);
for(int i = 0; i <= (n << 1); i++) d[i] = lower_bound(b + 1, b + sz + 1, d[i]) - b;
for(int i = 1; i <= m; i++){
int r1 = read(), r2 = read();
if(r1 > r2) swap(r1, r2);
if(!r1){ ans[i] = 0; continue; }
if(!isr[r1] || !isr[r2]){ ans[i] = 0; continue; }
if(d[r1] != d[r2]){ ans[i] = 0; continue; }
v[r1].pb(i);
}
bin[d[0]]++;
for(int i = 1; i <= (n << 1); i++){
for(int j = 0; j < v[i].size(); j++){
int id = v[i][j];
ans[id] = bin[d[i]];
} bin[d[i]]++;
}
for(int i = 1; i <= m; i++) cout << ans[i] << '\n';
}
return 0;
}
T3
题目描述
解析
题解
// Ho-kago Tea Time
#include <bits/stdc++.h>
using namespace std;
#define DEBUG(...) fprintf(stderr, __VA_ARGS__)
#define mp make_pair
#define fst first
#define snd second
#define SZ(u) ((int) (u).size())
#define ALL(u) (u).begin(), (u).end()
inline void proc_status()
{
ifstream t("/proc/self/status");
cerr << string(istreambuf_iterator<char>(t), istreambuf_iterator<char>()) << endl;
}
template<typename T> inline bool chkmin(T &a, const T &b) { return a > b ? a = b, 1 : 0; }
template<typename T> inline bool chkmax(T &a, const T &b) { return a < b ? a = b, 1 : 0; }
template<typename T> inline T read()
{
register T sum(0), fg(1);
register char ch(getchar());
for(; !isdigit(ch); ch = getchar()) if(ch == '-') fg = -1;
for(; isdigit(ch); ch = getchar()) sum = sum * 10 - '0' + ch;
return sum * fg;
}
typedef long long LL;
typedef pair<int, int> pii;
const int MAXN = (int) 1e6;
int n, m;
int p[MAXN * 2 + 5];
inline void input()
{
n = read<int>(), m = read<int>();
for(int i = 1; i <= 2 * n; ++i) p[i] = read<int>();
}
namespace TREE
{
const int MAX_NODE = MAXN * 2;
int l[MAXN * 2 + 5], r[MAXN * 2 + 5];
int fa[MAX_NODE + 5];
vector<int> adj[MAX_NODE + 5];
const int MAX_LOG = 20;
int rt[MAX_NODE + 5], dep[MAX_NODE + 5], anc[MAX_LOG + 1][MAX_NODE + 5];
inline void dfs(int u, int rt0)
{
rt[u] = rt0;
dep[u] = fa[u] == -1 ? 1 : dep[fa[u]] + 1;
anc[0][u] = fa[u];
for(int i = 1; (1 << i) < dep[u]; ++i) anc[i][u] = anc[i - 1][anc[i - 1][u]];
for(auto v : adj[u]) dfs(v, rt0);
}
inline void build()
{
static vector<int> stk;
stk.clear();
for(int i = 1; i <= 2 * n; ++i)
{
l[i] = min(i, p[i]);
r[i] = max(i, p[i]);
while(!stk.empty() && stk.back() >= l[i])
{
int p = stk.back();
stk.pop_back();
chkmin(l[i], l[p]);
chkmax(r[i], r[p]);
}
stk.push_back(i);
}
for(int i = 0; i <= 2 * n; ++i) rt[i] = fa[i] = -1;
for(int i = 1; i <= 2 * n; ++i) if(r[i] == i)
{
fa[i] = l[i] - 1;
adj[l[i] - 1].push_back(i);
}
r[0] = 0;
for(int i = 0; i <= 2 * n; ++i) if(!adj[i].empty() && rt[i] == -1) dfs(i, i);
}
inline int lca(int u, int v)
{
if(dep[u] < dep[v]) swap(u, v);
for(int k = dep[u] - dep[v], i = 0; (1 << i) <= k; ++i) if(k >> i & 1) u = anc[i][u];
if(u == v) return u;
for(int i = MAX_LOG; i >= 0; --i) if((1 << i) < dep[u] && anc[i][u] != anc[i][v]) u = anc[i][u], v = anc[i][v];
return fa[u];
}
inline int query(int r1, int r2) { return rt[r1] == -1 || rt[r2] == -1 || rt[r1] != rt[r2] ? 0 : dep[lca(fa[r1], fa[r2])]; }
}
inline void solve()
{
TREE::build();
while(m--)
{
int r1 = read<int>(), r2 = read<int>();
if(r1 == 0 || r2 == 0) puts("0");
else printf("%d\n", TREE::query(r1, r2));
}
}
int main()
{
freopen("hotchkiss.in", "r", stdin);
freopen("hotchkiss.out", "w", stdout);
input();
solve();
return 0;
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
