191024-模拟测试7
T1 Tom 传送门
1.1 题目描述
众所周知,Tom 猫对香肠非常感兴趣。 有一天,Tom 家里的女主人赏给了 Tom 一大堆香肠。这些香肠太多了,以至于 Tom 一顿吃不完, 于是它把这些香肠串成了一棵树,树的每个节点上都有一个香肠。 Tom 需要给这些香肠进行编号,其中有 a 个香肠需要编号为 1,2···a 中的不重复的编号,作为早餐 肠,剩下的 b 个香肠需要编号为 −1,−2···−b 中的不重复的编号,作为晚餐肠。 Tom 每天会随机吃一顿饭,可能是早饭,也可能是晚饭。如果是吃早饭,Tom 会吃掉编号绝对值最 小的早餐肠,反之吃掉编号绝对值最小的晚餐肠。 如果一根香肠被吃掉了,那么与它相连的树上的边都会断掉,因此剩下的香肠可能会因此变成若干 棵树,即变得不再连通。这是 Tom 不希望发生的事。 请给这些香肠编号,使得无论 Tom 如何安排早饭和晚饭,整棵树一直都是连通的。
1.2 输入描述
输入文件名为 tom.in。 第一行三个正整数 n,a,b,代表节点的数目,早餐肠的数目,晚餐肠的数目。保证 a + b = n。 第二行开始,共 n−1 行,每行两个正整数 u,v,代表树上一条边。
1.3 输出描述
输出文件名为 tom.out。 共 n 行,第 i 行输出第 i 个节点的编号。 如果存在多种编号方式,请随意输出一种。如果不存在这样的编号方式,请输出 −1。
分析
该题简而言之,给定一棵树和 a,b 两个数字,将每个节点编号为
1
,
2...
a
1,2...a
1,2...a 以及
−
1
,
−
2...
−
b
−1,−2...−b
−1,−2...−b中的一个,使得对于任 意的
x
≤
a
,
y
≤
b
x≤a,y≤b
x≤a,y≤b,树上
[
−
b
,
−
y
]
∪
[
x
,
a
]
[−b,−y]∪[x,a]
[−b,−y]∪[x,a] 编号的节点组成了一个联通块。
那么我们只需要找到一条断边,将原树分成两颗树,一棵树的size等于a,另一棵树等于b。因此首先dfs,求出每个子树的size,如果没有等于a或b的子树,便输出‘-1’,否则bfs实现染色,输出答案。
(考场上想到了正解,但不会求每棵子树的size,qwq)
反思
以后不要用next作为数组名,会关键字冲突
代码(自己写的)
#include<bits/stdc++.h>
using namespace std;
int size[500009],n,a,b,tot,next[500009],first[500009],to[500009],s[500009],fat[500009];
bool bj;
queue<int>q;
void add(int x,int y)
{
next[++tot]=first[x];
first[x]=tot;
to[tot]=y;
}
void gsize(int u,int fa)
{
size[u]=1;
for(int i=first[u];i;i=next[i])
{
int v=to[i];
if(v==fa)
continue;
fat[v]=u;
gsize(v,u);
size[u]+=size[v];
}
}
void bfs(int root,int num,int vis)//bfs染色;
{
while(!q.empty())
q.pop();
if(num==1)
{
q.push(root);
while(!q.empty())
{
int u=q.front();
s[u]=a;
a--;
q.pop();
for(int i=first[u];i;i=next[i])
{
int v=to[i];
if(vis==1&&fat[u]==v) continue;
if(s[v]) continue;
q.push(v);
}
}
}
else
{
q.push(root);
while(!q.empty())
{
int u=q.front();
s[u]=-b;
b--;
q.pop();
for(int i=first[u];i;i=next[i])
{
int v=to[i];
if(vis==1&&fat[u]==v) continue;
if(s[v]) continue;
q.push(v);
}
}
}
}
int main()
{
int x,y;
scanf("%d%d%d",&n,&a,&b);
for(int i=1;i<=n-1;i++)
{
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
gsize(1,0);//找每个子树的节点
for(int i=1;i<=n;i++)
{
if(size[i]==a)
{
bfs(i,1,1);
bfs(fat[i],2,2);
bj=1;
break;
}
if(size[i]==b)
{
bfs(i,2,1);
bfs(fat[i],1,2);
bj=1;
break;
}
}
if(!bj)
{
printf("-1\n");
return 0;
}
for(int i=1;i<=n;i++)
printf("%d ",s[i]);
return 0;
}
std
#include <algorithm>
#include <assert.h>
#include <iostream>
#include <cstring>
#include <vector>
#include <cstdio>
#include <cmath>
using namespace std;
const int MX = 200005;
template <typename T> void read(T &x)
{
x = 0; char c = getchar(); bool f = 0;
while(!isdigit(c) && c!='-') c = getchar();
if(c == '-') f = 1, c = getchar();
while(isdigit(c)) x = x*10+c-'0', c = getchar();
if(f) x = -x;
}
int n, num1, num2;
int fst[MX], nxt[MX], v[MX], lnum;
void addeg(int nu, int nv)
{
nxt[++lnum] = fst[nu];
fst[nu] = lnum;
v[lnum] = nv;
}
void input()
{
int a, b;
read(n), read(num1), read(num2);
assert(num1+num2 == n);
for(int i=1; i<n; i++)
{
read(a), read(b);
addeg(a, b);
addeg(b, a);
}
}
int siz[MX], fa[MX], id[MX];
void gsize(int x, int f)
{
siz[x] = 1, fa[x] = f;
for(int i=fst[x]; i; i=nxt[i])
if(v[i] != f)
gsize(v[i], x), siz[x] += siz[v[i]];
}
void print(int x, int f, int *val, int del)
{
for(int i=fst[x]; i; i=nxt[i])
if(v[i] != f)
print(v[i], x, val, del);
(*val) += del;
id[x] = (*val);
}
void work()
{
bool ok = 0;
gsize(1, 0);
for(int i=1; i<=n; i++)
{
if(siz[i] == num1)
{
int x = 0;
print(i, fa[i], &x, +1);
x = 0;
print(fa[i], i, &x, -1);
ok = 1;
}
else if(siz[i] == num2)
{
int x = 0;
print(i, fa[i], &x, -1);
x = 0;
print(fa[i], i, &x, +1);
ok = 1;
}
}
if(!ok) printf("-1");
else for(int i=1; i<=n; i++) printf("%d ", id[i]);
putchar('\n');
}
int main()
{
freopen("tom.in", "r", stdin);
freopen("tom.out", "w", stdout);
input();
work();
return 0;
}
思考
如果求合法的方案数,应该怎么求?
T2 Jerry 传送门
2.1 题目描述
众所周知,Jerry 鼠是一只非常聪明的老鼠。 Jerry 聪明到它可#以计算 64 位有符号整形数字的加减法。 现在,Jerry 写下了一个只由非负整数和加减号组成的算式。它想给这个算式添加合法的括号,使得 算式的结果最大。这里加减法的运算优先级相同,和我们在日常生活中接触到的一样,当没有括号时,先 算左边的,再算右边的。 比如,算式 ((1 + 2) + 3−(4−5)) + 6 是合法的,但是 )1 + 2( 和 (−)1 + 2 以及 −(1) + 2 都是不合 法的。
2.2 输入描述
输入文件为 jerry.in。 第一行一个整数 T,代表数据组数。 接下来,共有 T 组数据,每组的格式如下: 第一行一个整数 n,代表数字的个数。 接下来一行共 2n−1 个符号或非负整数,组成一个由空格隔开的算式。
2.3 输出描述
输出文件为 jerry.out。 一行一个整数,代表添加括号后,算式最大的可能结果。
分析
算法一
对于 n ≤ 3 的测试点,如果我们手动预处理可能的添加括号的方法,然后用机器暴力求出每一种括 号添加方式下某个算式的答案,复杂度是 O ( n ) O(n) O(n) 的。 这样做可以获得10分。(考场上写的)
算法二
我们用机器枚举添加括号后每一个运算符的计算顺序,即可得到一种 O ( n ! ) O(n!) O(n!) 的算法,获得 30 分。(没写出来,qwq)
算法三
整个算式在添加完括号后可以用表达式树进行计算,因此我们可以用状态去表示表达式树的形态,进行Dp。 如果我们用 f ( i , j ) , g ( i , j ) f(i,j),g(i,j) f(i,j),g(i,j) 分别表示区间 [ i , j ] [i,j] [i,j] 内的算式获得的最大值和最小值,我们可以得到一种 O ( n 3 ) O(n^3) O(n3) 的区间 Dp 算法。 对于区间 [ i , j ] [i,j] [i,j],我们枚举这个区间内最后一个被计算的算符 k,从而 f ( i , j ) f(i,j) f(i,j)可以从 f ( i , k − 1 ) f(i,k −1) f(i,k−1) 和 f ( k + 1 , j ) f(k + 1,j) f(k+1,j) 转移过来。 空间复杂度 O ( n 3 ) O(n^3) O(n3),这样可以获得 50 分。
算法四
注意到一对括号如果添加在正号后面,没有任何作用,添加在负号后面则可以将一段区间内的数字 取反。 而最后的答案实际上就是按照正负号将对应的数取反后,再将算式中所有的数加起来。 受到这一点的启示,我们可以得到一个 O ( n 2 ) O(n^2) O(n2) 的 Dp。 用 f ( i , j ) f(i,j) f(i,j) 表示,在序列的前 i 个数中,添加的括号中还有 j 个左括号没有对应的右括号,这时这 i 个数字按照对应的正负性加起来后得到的结果最大值。 根据 j 的奇偶性转移即可。
算法五
实际上,括号嵌套的最大层数不需要超过 2。因为 2 层括号已经可以让第一层括号内所有可以变成 正数的数子全部变成正的,再添加括号没有意义。 这样,我们就可以把算法四的复杂度优化成 O ( n ) O(n) O(n)了。
算法六 详细解析wyh传送
结论1,在正数前后加上括号,都不会对答案有任何贡献(因为 括号最本质的作用即符号取反)
应用:由结论1,我们可以将连续正数全部合并,那么式子将变为正负负正负正
结论二,在负数前添括号时,我们分以下两种情况讨论
1,
a
[
i
]
<
0
,
a
[
i
+
1
]
>
0
a[i]<0,a[i+1]>0
a[i]<0,a[i+1]>0 对于这种情况,我们有两种选择,一种是
a
[
i
+
1
]
>
s
u
m
[
i
+
2
,
i
+
3...
]
a[i+1]>sum[i+2,i+3...]
a[i+1]>sum[i+2,i+3...],那么我们不加括号,否则我们加上括号
2,
a
[
i
]
<
0
,
a
[
i
+
1
]
<
0
a[i]<0,a[i+1]<0
a[i]<0,a[i+1]<0 对于这种情况,我们可以将后面的数全部变为正贡献加入答案中
以下参考的fsy的解析

代码 算法5
#include<bits/stdc++.h>//该dp前提条件,每个‘-’前都必须加上一个左括号;
# define INF 1e18;
using namespace std;
long long n,m,t,num[1000009],con[1000009],f[1000009][3];
int read(){
int x = 0,f = 1;
char ch = getchar();
while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)) {x = (x<<3) + (x<<1) + ch - '0'; ch = getchar();}
return x * f;
}
int main()
{
scanf("%lld",&t);
for(int cas=1;cas<=t;cas++)
{
scanf("%lld",&n);
con[1] = 1;
for(int i = 1;i <= n;++i)
{
num[i] = read();
if(i != n)
{
char ch = getchar();
while(ch != '+' && ch != '-') ch = getchar();
if(ch == '+') con[i+1] = 1;
else con[i+1] = -1;
}
}
f[0][0]=0;
f[0][1]=-INF;
f[0][2]=-INF;
for(int i=1;i<=n;i++)
{
if(con[i]==1)
{
f[i][0]=max(max(f[i-1][1]+num[i],f[i-1][0]+num[i]),f[i-1][2]+num[i]);
f[i][1]=max(f[i-1][1]-num[i],f[i-1][2]-num[i]);
f[i][2]=f[i-1][2]+num[i];
}
else
{
f[i][0]=-INF;//强制使‘-’后加一个括号 ,即使后面该情况不是最优,也会在后面被更新掉,如:-(5) 不是最优就在该数字后直接括回来;
f[i][1]=max(max(f[i-1][0]-num[i],f[i-1][2]-num[i]),f[i-1][1]-num[i]);
f[i][2]=max(f[i-1][2]+num[i],f[i-1][1]+num[i]);
}
}
printf("%lld\n",max(max(f[n][0],f[n][2]),f[n][1]));
}
return 0;
}
算法6(参考自gigo_64)
//太多括号没用。括号意味着取反。
//一个负号后面有两种。一种是舍弃下一个,其它都为正。反正第三位开始所有数字都可以取正。
//反着动规即可
#include<bits/stdc++.h>
using namespace std;
#define in read()
#define int long long
int in{
int cnt=0,f=1;char ch=0;
while(!isdigit(ch)){
ch=getchar();if(ch=='-')f=-1;
}
while(isdigit(ch)){
cnt=cnt*10+ch-48;
ch=getchar();
}return cnt*f;
}
int t,n;
char ch[500003];
int f[200003];
int a[200003];int cnt;int b[200003];
int sum[200003];
signed main(){
t=in;
while(t--){
n=in;for(int i=1;i<=n;i++)f[i]=0;cnt=0;
for(int i=1;i<=n;i++)a[i]=in;a[0]=-1;
for(int i=1;i<=n;i++){
if(a[i]<0)b[++cnt]=a[i];
else if(a[i-1]<0)b[++cnt]=a[i];
else b[cnt]+=a[i];
}
//for(int i=1;i<=cnt;i++)cout<<b[i]<<" ";cout<<endl;
sum[cnt+1]=0;
for(int i=cnt;i>=1;i--){
sum[i]=sum[i+1];if(b[i]>=0)sum[i]+=b[i];else sum[i]-=b[i];
}
//for(int i=1;i<=cnt;i++)cout<<sum[i]<<" ";cout<<endl;
f[cnt]=b[cnt];
for(int i=cnt-1;i>=1;i--){
if(b[i]>=0)f[i]=b[i]+f[i+1];
else{
if(b[i+1]<0)f[i]=b[i]+sum[i+1];
else{
f[i]=max(f[i+1]+b[i],b[i]-b[i+1]+sum[i+2]);
}
}
}
cout<<f[1]<<'\n';
}
return 0;
}
T3 speike 传送门
3.1 题目描述
众所周知,Speike 狗是一条特别喜欢追着 Tom 打的狗。 现在,Tom 又把 Speike 惹生气了,现在 Speike 需要跨越千山万水找 Tom 报仇。 Speike 所在的世界可以看成是一个无穷大的平面,平面由一个平面直角坐标系确定。在平面上有许 多不相交的矩形障碍,矩形的四边平行于坐标轴。 Speike 需要从 (0,0) 出发,按恒定的速率在尽量短的时间内跑到 (Xt,0),也就是 Tom 在的位置。出 题人规定,Speike 只能沿着平行于坐标轴的方向运动,且不能进入矩形障碍的内部,但是可以在障碍边界上移动。 所有障碍的横坐标都在 [ 0 , X t ] [0,X_t] [0,Xt] 之内。保证矩形不相交 (即没有公共面积,或者说公共面积为 0,但是 可能共享一条边或者一个顶点),也不会退化成线段或者点。 Speike 的智商不是很高,因此他需要你帮忙设计一条最短的路线。当然,你只需要告诉他路线的长度就行了。
3.2 输入描述
输入文件名为 speike.in。 第一行一个整数 n,代表障碍的个数。 第二行一个整数 Xt,代表终点的横坐标。 第三行开始,共 n 行,每行 4 个整数 a,b,c,d,代表每个矩形的某两个相对的顶点的坐标为 ( a , b ) (a,b) (a,b) 和 ( c , d ) (c,d) (c,d)。
3.3 输出描述
输出文件名为 speike.out。 共一行,一个整数,代表最短路线的长度。
分析
首先第一眼看过去,贪心!但其实随便验证一下,就可以证明其错误性(但贪心可以拿25分)如下图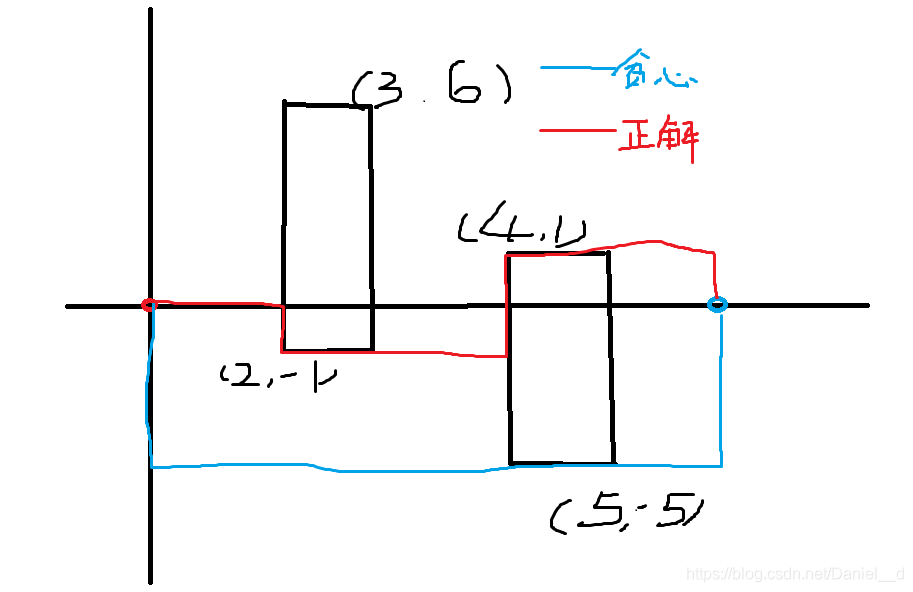
3.2 算法一
直接建立出网格图,将障碍内部的边删除,进行网格图最短路,复杂度为 O ( X 2 ) O(X^2) O(X2)。 可以获得 45 分。(考场上竟然没想到,qwq)
3.3 算法二
我们发现,为了让路程尽量短,我们的路径会尽量贴着障碍走。 我们尝试用折线将所有障碍的顶点连接起来,如果两个点之间的折线被其它障碍遮挡,则不连这条线。然后在折线连成的图上做最短路。 结合算法 1 可以得到 65 分。
3.4 算法三
• 引理 1:存在一条最短路,其 x 坐标单调递增。
• 证明 1:如果存在 x 坐标不单调递增的地方,通过画图,我们可以清楚地知道,要么两个矩形相交了,要么还存在一条更短的路。
• 引理 2:存在一条最短路,满足引理 1 的性质,同时只在矩形的边界处拐弯。
• 证明 2:任何一个不在矩形边界处拐弯的最短路,都可以通过平移拐弯的地方,使得每个拐弯处都 在矩形边界上,同时路程长度不变。
有了这两个引理,我们就可以采用扫描线来求出最短路。 用
f
(
x
,
y
)
f(x,y)
f(x,y) 表示
(
0
,
0
)
(0,0)
(0,0)走到
(
x
,
y
)
(x,y)
(x,y) 的最短路长度。根据引理 1,按照 x 递增的顺序可以正确地求出 f。 f 应该怎么转移呢? 根据引理 2,没有障碍时,一条水平的路径上,
f
(
x
,
y
)
=
f
(
x
−
1
,
y
)
f(x,y) = f(x−1,y)
f(x,y)=f(x−1,y)。 遇到障碍的左边界时,水平的路径为了绕过障碍,
f
(
x
,
y
)
=
m
i
n
(
f
(
x
,
y
+
1
)
,
f
(
x
,
y
−
1
)
)
f(x,y) = min(f(x,y + 1),f(x,y−1))
f(x,y)=min(f(x,y+1),f(x,y−1))。 上面的讨论没有涉及到障碍的右边界,因此每一个矩形只需要保留左边界即可。 当算法开始时,我们只知道
f
(
0
,
0
)
=
0
f(0,0) = 0
f(0,0)=0。然后,依次对于每个障碍
(
x
i
,
[
l
,
r
]
)
(xi,[l,r])
(xi,[l,r]),我们找到所有
l
≤
y
≤
r
l ≤ y ≤ r
l≤y≤r 的
f
(
x
,
y
)
f(x,y)
f(x,y),并用他们来更新 f(xi,l) 和 f(xi,r)。处理完所有的障碍后,用剩下的
f
(
x
,
y
)
f(x,y)
f(x,y) 更新
f
(
X
,
0
)
f(X,0)
f(X,0) 即 可得到答案。在算法中 f 可以用一个 set 来保存,根据分析,这个 set 的大小不会超过 n。 这样的时间复杂度为
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)。
代码 暴力建图(不完善)
#include<bits/stdc++.h>//(暴力建图:只能解决所有矩形与x轴相交的情况)
using namespace std;
int xt,n,next[100009],to[100009],w[100009],first[100009],dis[100009],tot,a,b,c,d;
void add(int x,int y,int z)
{
next[++tot]=first[x];
first[x]=tot;
to[tot]=y;
w[tot]=z;
}
struct zb
{
int x,y,z;
}e[200009];
bool comp(const zb &a,const zb &b)
{
return a.x<b.x;
}
void spfa()
{
queue<int>q;
memset(dis,127,sizeof(dis));
dis[0]=0;
q.push(0);
while(!q.empty())
{
int v=q.front();
q.pop();
for(int i=first[v];i;i=next[i])
{
int u=to[i];
if(dis[u]>dis[v]+w[i])
{
dis[u]=dis[v]+w[i];
q.push(u);
}
}
}
}
int main()
{
scanf("%d%d",&n,&xt);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d%d",&a,&b,&c,&d);
e[i].x=a;
e[i].y=b;
e[i].z=d;
}
sort(e+1,e+n+1,comp);
add(0,1,abs(e[1].y));
add(0,2,abs(e[1].z));
for(int i=1;i<n;i++)
{
add(2*i-1,2*i+1,abs(e[i+1].y-e[i].y));
add(2*i-1,2*i+2,abs(e[i].y-e[i+1].z));
add(2*i,2*i+1,abs(e[i+1].y-e[i].z));
add(2*i,2*i+2,abs(e[i].z-e[i+1].z));
}
add(2*n-1,2*n+1,abs(e[n].y));
add(2*n,2*n+1,abs(e[n].z));
spfa();
printf("%d",dis[2*n+1]+xt);
return 0;
}
正解
#include<bits/stdc++.h>
using namespace std;
#define in read()
inline int in
{
int cnt=0,f=1;char ch=0;
while(!isdigit(ch)){
ch=getchar();if(ch=='-')f=-1;
}
while(isdigit(ch))
{
cnt=cnt*10+ch-48;
ch=getchar();
}
return cnt*f;
}
struct node
{
int l,r,tag,key;
}t[5000003];
int pre[1000003][2];
int f[1000003][2];
int n,end;
struct Line
{
int down,up,x;
}line[1000003];
int lcnt;
int bb[4000003],bcnt,len;
inline bool linecm(Line a,Line b)
{
if(a.x!=b.x) return a.x<b.x;
if(a.down!=b.down) return a.down<b.down;
return a.up<b.up;
}
inline void build(int u,int l,int r)
{
t[u].l=l;
t[u].r=r;
if(l==r)
return;
int mid=(l+r)/2;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
}
inline void pushdown(int u)
{
if(t[u].tag)
{
t[u*2].tag=t[u*2+1].tag=t[u].tag;
t[u*2].key=t[u*2+1].key=t[u].tag;
t[u].tag=0;
}
}
inline void modify(int u,int ql,int qr,int key)
{
if(t[u].r<ql||t[u].l>qr) return;
if(ql<=t[u].l&&t[u].r<=qr)
{
t[u].tag=t[u].key=key;
return;
}pushdown(u);
modify(u*2,ql,qr,key);
modify(u*2|1,ql,qr,key);
}
inline int query(int u,int pos)
{
if(t[u].l==t[u].r&&t[u].r==pos) return t[u].key;
pushdown(u);
int mid=(t[u].l+t[u].r)/2;
if(pos<=mid) return query(u*2,pos);
else return query(u*2|1,pos);
}
int main()
{
memset(f,127,sizeof(f));
n=in;end=in;
line[++lcnt]={0,0,0};
line[++lcnt]={0,0,end};
for(int i=1;i<=n;i++)
{
int a=in,b=in,c=in,d=in;
if(b<d) swap(b,d);bb[++bcnt]=b;bb[++bcnt]=d;
line[++lcnt]={d,b,a};
}
bb[++bcnt]=0;
sort(line+1,line+lcnt+1,linecm);
sort(bb+1,bb+bcnt+1);
len=unique(bb+1,bb+bcnt+1)-bb-1;//去重,返回值为去重后数组的长度;
for(int i=1;i<=lcnt;i++)
{
line[i].down=lower_bound(bb+1,bb+len+1,line[i].down)-bb;
line[i].up=lower_bound(bb+1,bb+len+1,line[i].up)-bb;
}
for(int i=2;i<=lcnt;i++)
{
if(line[i].x) break;
if(!bb[line[i].down]&&!bb[line[i].up])
{
swap(line[i],line[1]);
break;
}
}
build(1,1,len);
for(int i=1;i<=lcnt;i++)
{
pre[i][0]=query(1,line[i].down);
pre[i][1]=query(1,line[i].up);
modify(1,line[i].down,line[i].up,i);
}
f[1][0]=f[1][1]=0;
for(int i=2;i<=lcnt;i++)
{
int p=max(1,pre[i][0]);
f[i][0]=min(f[p][0]+abs(bb[line[i].down]-bb[line[p].down]),f[p][1]+abs(bb[line[i].down]-bb[line[p].up]));
p=max(1,pre[i][1]);
f[i][1]=min(f[p][0]+abs(bb[line[i].up]-bb[line[p].down]),f[p][1]+abs(bb[line[i].up]-bb[line[p].up]));
}
printf("%d",f[lcnt][0]+end);
return 0;
}





















 361
361

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








