概率论与数理统计

课程地址

中心极限定理

描述任何统计数据分布：中心，分散度，形状

对于有限个独立同分布的随机变量X1,X2,X3…Xn，则其平均值服从正态分布：
$$\overline{X}\sim N(\mu ,\frac{{\sigma }^2}{n})$$

举一个例子，假设在一个学校中，每个班有 30 人，一共有 100 个班。如果我们对每个班的学生都求平均身高，就能得到 100 个班学生平均身高，这 100 个平均身高就服从正态分布

直觉而言，这 100 个平均身高的平均值，应该等于总体的平均值，而其标准差应该小于总体的标准差（总体应该比局部更分散，这也就解释了上面的 ${\sigma }^2/n$）

中心极限定理是说无论总体数据服从什么分布，其样本均值都服从正态分布，且随着样本数目的增加，该正态分布的方差会减小，也就是曲线愈发集中

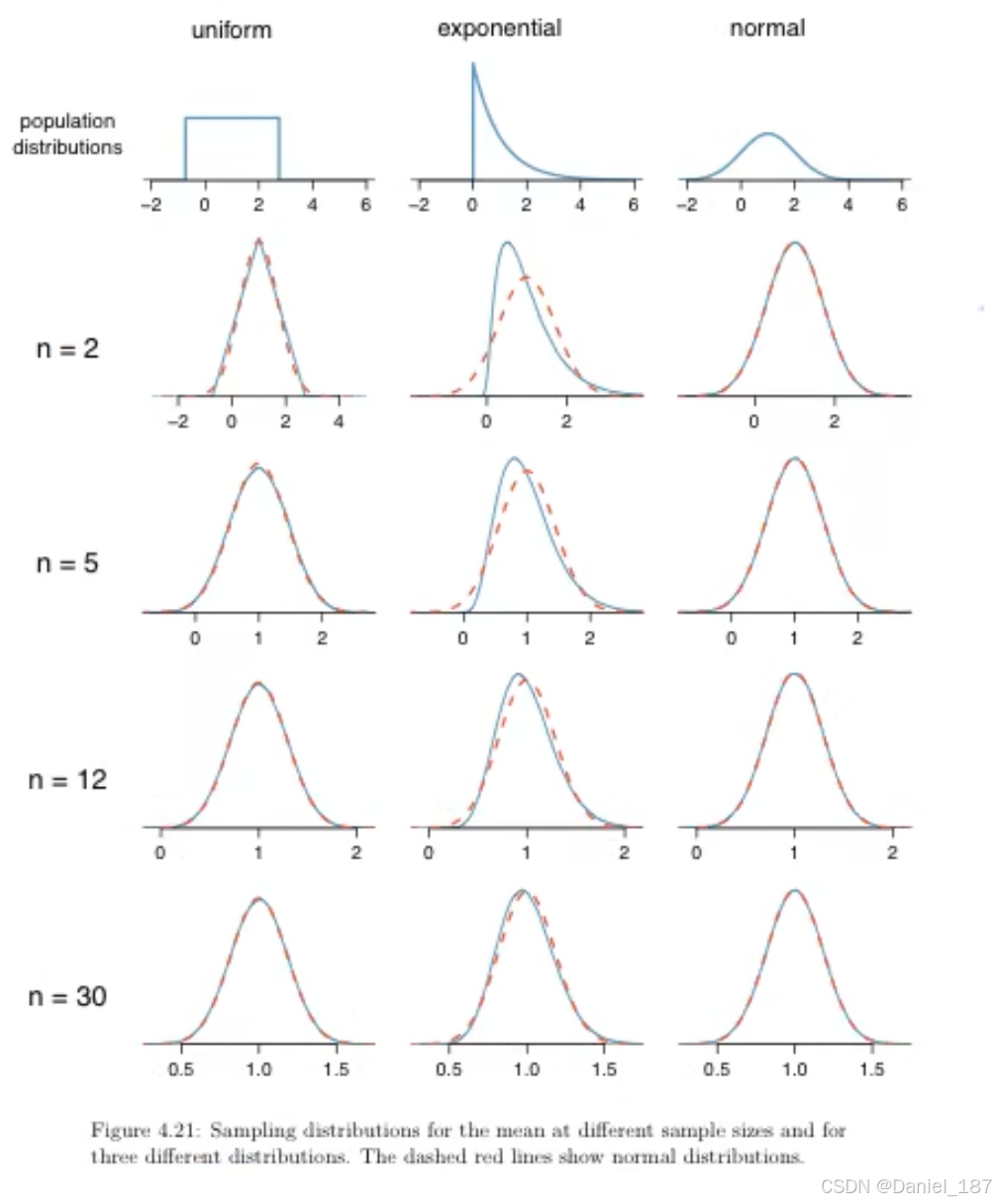
将其转化为标准正态分布：

$$Z=\frac{\overline{X}-\mu }{\frac{\sigma }{\sqrt{n}}}\sim N(0,1)$$

---

正态分布

Z值和Z分布：

$$Z=\frac{X-\mu }{\sigma }\sim N(0,1)$$

3sigma原则：

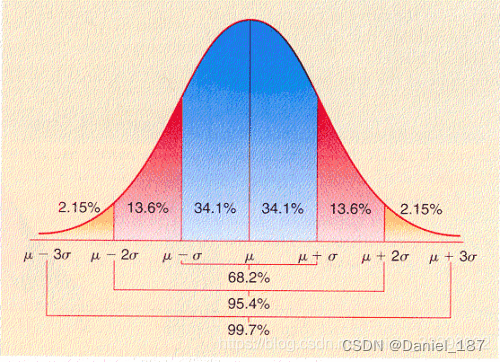
例题：

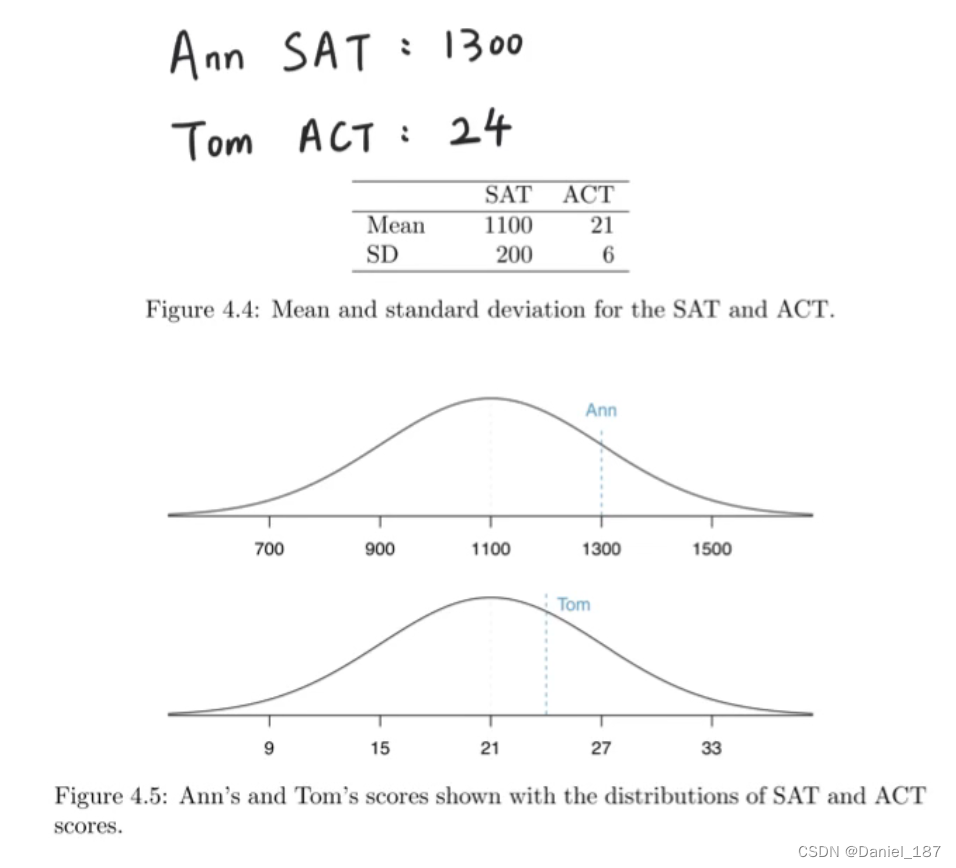
Ann: (1300-1100)/200=1

Tom: (24-21)/6=0.5

所以Ann的成绩更好

---

二项分布

n次伯努利事件发生r次的概率：

$$P(x=r)=\left(\genfrac{}{}{0ex}{}{n}{r}\right)p^r(1-p{)}^{n-r}$$

伯努利事件：独立可重复；只有两种结果

性质：$E(X)=np$，$D(X)=np(1-p)$

当n值较大时，如何估计二项分布：
若np>10：可以用正态分布来近似二项分布
若np<10：可以用泊松分布来近似二项分布

一个排列的经典问题：mississippi有多少种排列方式？

$$\frac{11!}{4!\ast 4!\ast 2!}$$

---

泊松分布和指数分布

泊松分布：描述一段时间内，事件发生多少次的概率分布：

$$P(X=k)=\frac{{\lambda }^k}{k!}{e}^{-\lambda }$$

$E(X)=\lambda$，$D(X)=\lambda$

指数分布：描述事件与事件之间间隔时间的概率分布：

$$\Phi (x)=\lambda e^{-\lambda x}$$

其中lambda和x均>0

$E(X)=\frac{1}{\lambda }$，$D(X)=\frac{1}{{\lambda }^2}$

例题，排队理论：

---

t分布

t分布的定义：

设$X\sim N(0,1)$，$Y\sim {\chi }^2(n)$，且X与Y相互独立，则称随机变量
$$T=\frac{X}{\sqrt{Y/n}}$$
服从自由度为n的t分布，记为$T\sim t(n)$

t分布的提出是作为正态分布的修正

根据中心极限定理和Z分布，n个独立同分布的随机变量，其平均值服从正态分布：

$$\overline{X}\sim N(\mu ,\frac{{\sigma }^2}{n})$$

$$Z=\frac{\overline{X}-\mu }{\frac{\sigma }{\sqrt{n}}}\sim N(0,1)$$

但是由于在上式中总体的标准差很难得到，所以一般用样本的方差替换总体的标准差，得到统计量t，它服从t分布，又称student分布：

$$t=\frac{\overline{X}-\mu }{\frac{S}{\sqrt{n}}}\sim t(n-1)$$

自由度为n-1，n为样本数量，下图为不同自由度的t分布图像

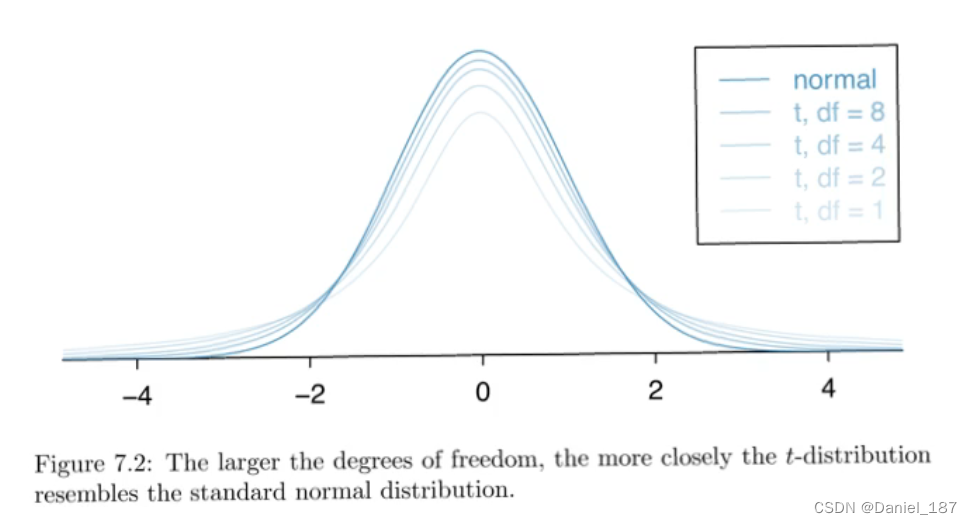
与标准正态分布而言，t分布的特征为“尖峰肥尾”

例题：

探究女性吸烟对胎儿体重的影响：

H0：吸烟对胎儿体重无影响，即u1-u2=0
H1：有影响，即u1-u2!=0

求统计量
$$t=\frac{(\overline{X_1}-\overline{X2})-({\mu }_1-{\mu }_2)}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}$$

t=1.54, df=49，做双边检验，查表得p=0.13>0.05，所以H0没有导致小概率事件发生，我们不能拒绝原假设H0，因此认为吸烟对胎儿体重无影响

t分布表：https://www.w3cschool.cn/statistics/t_distribution_table.html

---

卡方分布

卡方分布的定义：n个相互独立且服从标准正态分布的随机变量的平方和服从卡方分布：

$$\sum _{i=1}^n{Z}_i^2=Z_1^2+Z_2^2+...+Z_n^2\sim {\chi }^2(n)，其中Z_i\sim N(0,1)$$

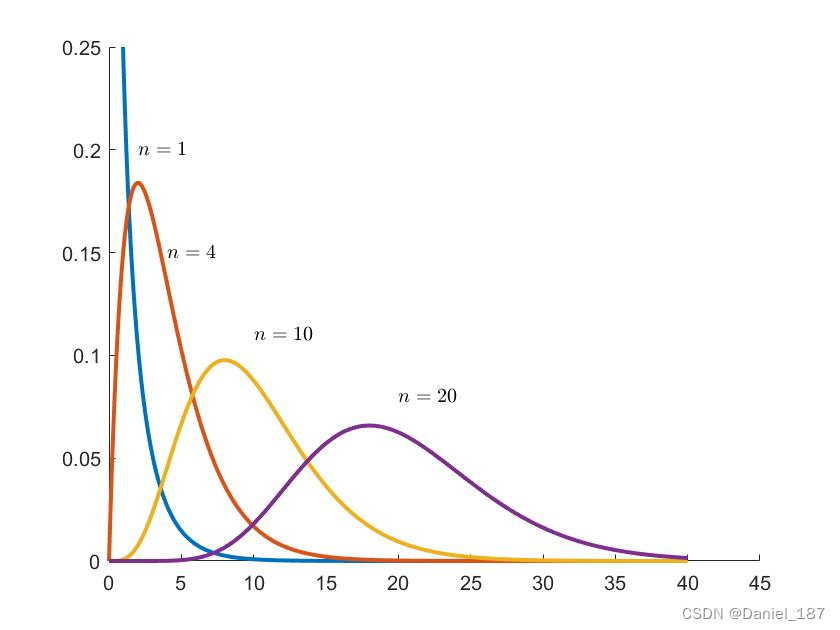
用来检验模型的适合性，变量的独立性等，对象是类别变量：

$${\chi }^2=\sum _{i=1}^n\frac{(O_i-E_i{)}^2}{E_i}$$

Oi是观察数据，Ei是期望数据

1. 先对数据进行假设，假设其服从某一模型
2. 根据这个模型计算出数据应该有的样子Ei
3. 再根据现实中观察到的数据Oi与之进行比较（套用上面的公式）

如果得到的结果过大，则说明观测到的值与期望的值相差过大，原来的假设不合理

例题：

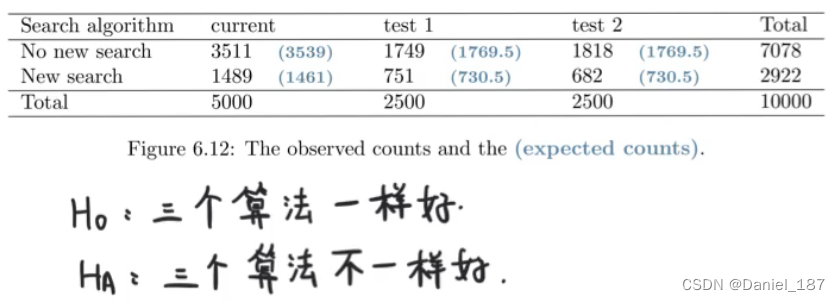
No new search：good；New search：bad

三个算法一样好<=>数据成比例分布

计算卡方值：

自由度$$df=(Row-1)\ast (Column-1)$$

查表得p=0.047<0.05，H0假设不成立

---

F分布和方差分析

F分布的数学定义：设U和V是相互独立的随机变量，$U\sim {\chi }^2(n_1),V\sim {\chi }^2(n_2)$，则称随机变量

$$F=\frac{U/n_1}{V/n_2}$$

服从自由度为$(n_1,n_2)$的F分布，记为$F\sim F(n_1,n_2)$。

其概率密度图如下：

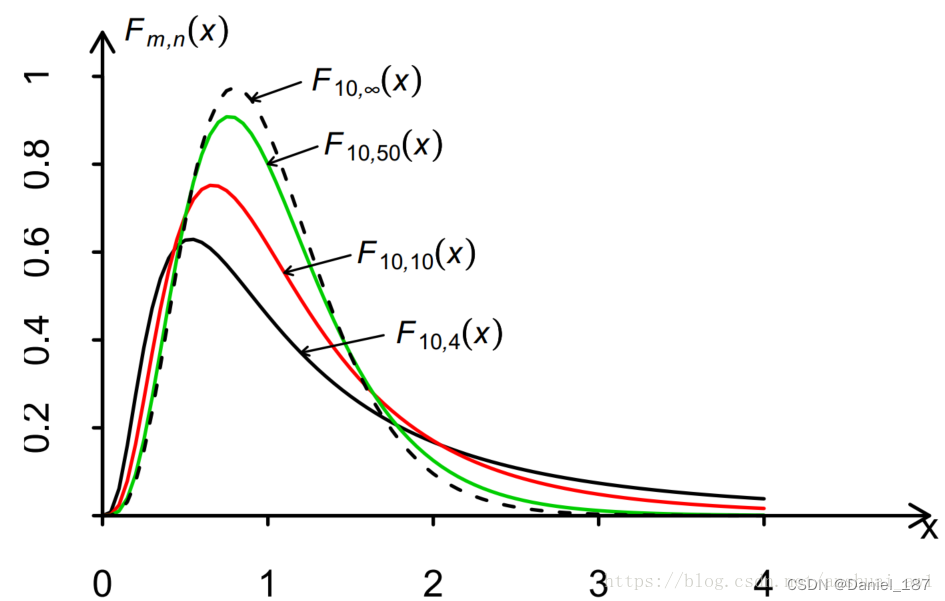
主要用来做多总体均值（三个及三个以上）的比较：analysis of variance-Anova

SSB=sum of square between group，组间平均差异
SSW=sum of square between group，组内平均差异

1. H0：u1=u2=…=un；H1：u1, u2,…,un不全相等
2. 求统计量$F=\frac{SSB/(n-1)}{SSW/(m-n)}\sim F(n-1,m-n)$，查表判断是否导致了小概率事件发生，从而推翻H0
   其中n为组数，m为样本量

F检验图：

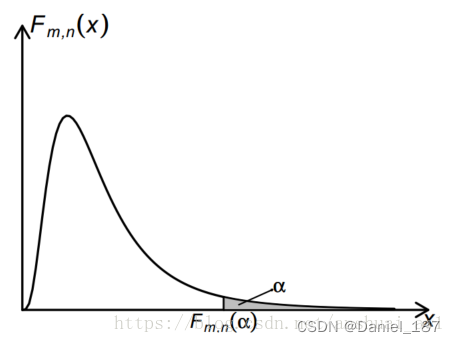
F值的求法：

1. 把n组数据放在一起，看成一个总体，算出这个总体的平均值u
2. 计算出每个组的组内平均值u1,u2,u3…un
3. 计算出组间平均差异$SSB=n_1(u_1-u{)}^2+n_2(u_2-u{)}^2+...+n_n(u_n-u{)}^2$
4. 计算出组内平均差异$SSW={\sum }_{i=1}^{n_1}(x_{1i}-u_1{)}^2+{\sum }_{i=1}^{n_2}(x_{2i}-u_2{)}^2+...+{\sum }_{i=1}^{n_n}(x_{ni}-u_n{)}^2$
5. $F=\frac{SSB/(n-1)}{SSW/(m-n)}\sim F(n-1,m-n)$

例题：

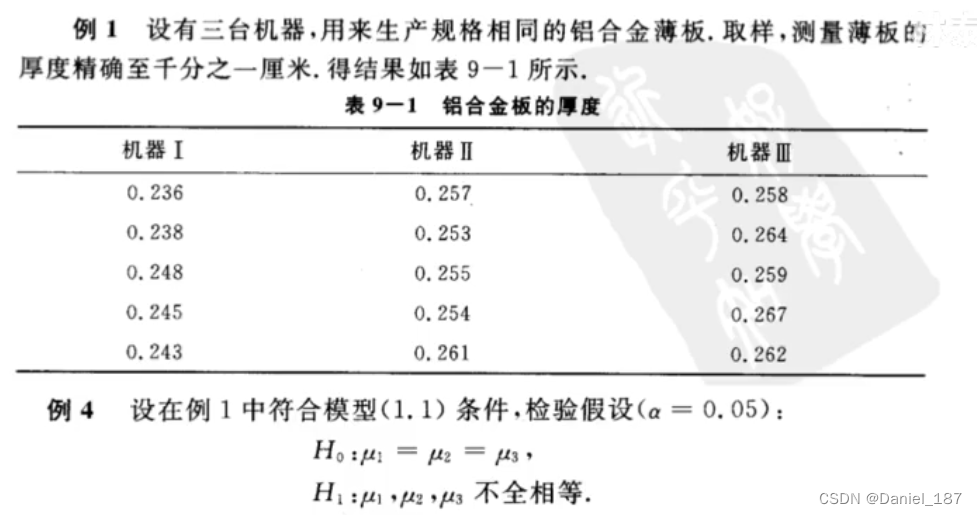
解：

u=0.253, u1=0.242, u2=0.256, u3=0.262
SSB=0.00105333
SSW=0.000192
F=32.9~F(2,12)
在0.05的显著性水平下，F(2,12)=3.89<32.9，故拒绝H0，因此认定各台机器生产的薄板厚度有显著差异

---

置信区间

考察全校学生的平均身高，抽取n=30的样本，计算得到样本均值u=170，如何获取总体的均值？

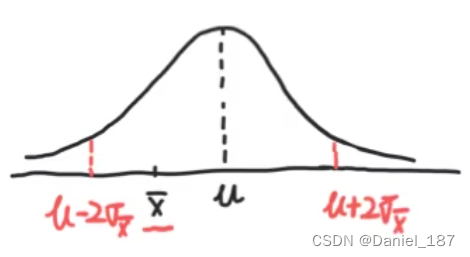
根据中心极限定理，$\overline{X}\sim N(\mu ,\frac{{\sigma }^2}{n})$，由正态分布的3sigma原则，我们有95%的把握认为：

$$\mu -2\frac{\sigma }{\sqrt{n}}\le \overline{X}\le \mu +2\frac{\sigma }{\sqrt{n}}$$
将不等式变形得到，我们有95%的把握认为：
$$\overline{X}-2\frac{\sigma }{\sqrt{n}}\le \mu \le \overline{X}+2\frac{\sigma }{\sqrt{n}}$$

对于单个正态分布总体的均值和方差的区间估计：

当${\sigma }^2$已知时，u的置信水平为1-$\alpha$的置信区间：

P { − Z α / 2 ≤ X ‾ − μ σ n ≤ Z α / 2 } = P { X ‾ − Z α / 2 σ n ≤ μ ≤ X ‾ + Z α / 2 σ n } = 1 − α P\{-Z_{\alpha/2}\le\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\le Z_{\alpha/2}\}\\=P\{\overline{X}-Z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\le\mu\le\overline{X}+Z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\}=1-\alpha P{−Zα/2​≤n ​σ​X−μ​≤Zα/2​}=P{X−Zα/2​n ​σ​≤μ≤X+Zα/2​n ​σ​}=1−α

当${\sigma }^2$未知时，使用t分布估计

---

假设检验

假设检验的思想：在目前的声称下，现实中观察到的事件的发生概率有多小

如果认为H0正确，导致了小概率事件的发生，我们就有理由推翻H0（小概率事件在一次试验中几乎不可能发生）

例题：某工厂生产一批钢材，已知这种钢材强度X服从正态分布$X\sim N(\mu ,{\sigma }^2)$，今从中抽取6件，测得数据如下：48.5, 49.0, 53.5, 49.5, 56.0, 52.5。问能否认为这批钢材的平均强度为52？

解：
H0：u=52；H1：u!=52

总体标准差未知，构造统计量$t=\frac{\overline{X}-\mu }{S/\sqrt{n}}\sim t(6-1)$

查表得$t_{0.05/2}(5)=2.571$，由此确定H0的拒绝域：|t|>2.571

求得$\overline{X}=51.5，s^2=8.9$，求得统计量t=0.41

t落在拒绝域之外，故应该接受H0假设，能认为这批钢材的平均强度为52

---

协方差和相关系数

协方差刻画了X和Y的同增同减的程度（正相关），相关系数用两个变量的标准差将其归一化

协方差：$Cov(X,Y)=E\{[X-E(X)]\ast [Y-E(Y)]\}$

相关系数：$\rho =\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$

---

均匀分布

若连续型随机变量X的概率密度函数为$f(x)$，则其数学期望定义为：$E(X)={\int }_{-\infty }^{+\infty }xf(x)\mathrm{d}x$

方差定义为：$D(X)=Var(X)=E\{[X-E(X){]}^2\}=E(X^2)-[E(X){]}^2$

对于概率密度为$f(x)$的连续型随机变量，其方差的计算公式为：

$$D(X)={\int }_{-\infty }^{+\infty }[x-E(X){]}^{2}f(x)\mathrm{d}x$$

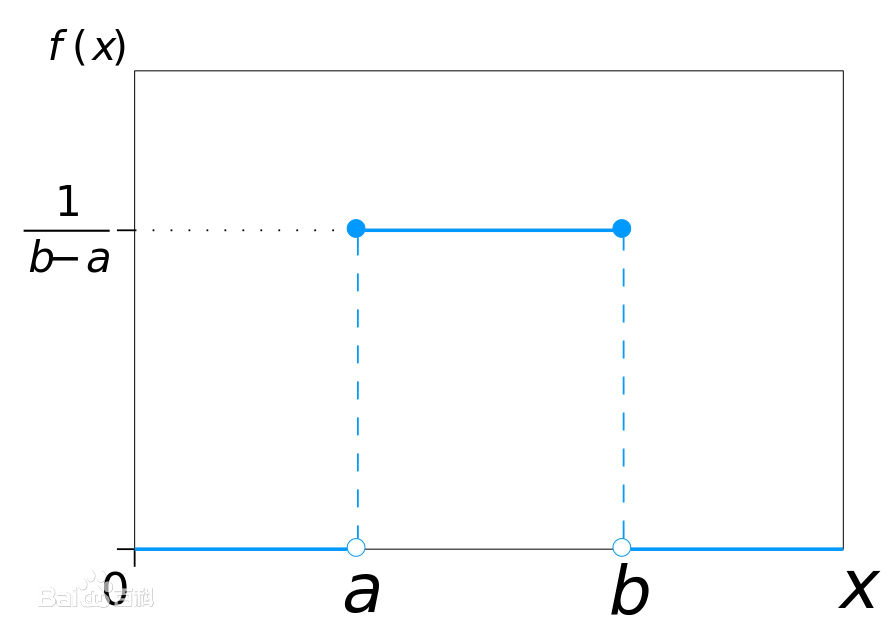
均匀分布的期望为$\frac{a+b}{2}$，方差为$\frac{(b-a{)}^2}{12}$（b-a刻画了数据的分散程度）

---

负二项分布

在伯努利实验中，成功的概率是p，一直做这个实验，直到得到第k次成功才停止，所需试验次数X的概率分布：

$$\begin{gathered} P(X=k)=\left(\genfrac{}{}{0ex}{}{n-1}{k-1}\right)p^{k-1}(1-p{)}^{n-k}p \\ =(\genfrac{}{}{0ex}{}{n-1}{k-1})p^k(1-p{)}^{n-k} \end{gathered}$$

期望：$E(X)=\frac{k}{p}$，方差：$D(X)=\frac{k(1-p)}{p^2}$

---

几何分布

在伯努利实验中，成功的概率是p，一直做这个实验，直到得到一次成功才停止，所需实验次数X的概率分布：

$$P(X=k)=(1-p{)}^{k-1}p$$

可见其概率分布是一个关于k的等比数列，因此得名几何分布

期望：$E(X)=\frac{1}{p}$，方差：$D(x)=\frac{1-p}{p^2}$

---

超几何分布

用于解决不放回的抽样问题：

$$P(x=3)=\frac{\left(\genfrac{}{}{0ex}{}{4}{3}\right)\left(\genfrac{}{}{0ex}{}{9}{2}\right)}{\left(\genfrac{}{}{0ex}{}{13}{5}\right)}=0.11$$
将问题一般化：

有N个小球，k个蓝色，N-k个红色，随机抽n个小球，每次抽一个且不放回，问抽到x个蓝球的概率

$$P(X=x)=\frac{\left(\genfrac{}{}{0ex}{}{k}{x}\right)\left(\genfrac{}{}{0ex}{}{N-k}{n-x}\right)}{\left(\genfrac{}{}{0ex}{}{N}{n}\right)}$$

当n<<N，超几何分布近似二项分布

期望：$E(X)=np$，方差$D(X)=\frac{N-n}{N-1}np(1-p)$

---

伯努利分布

又称0-1分布

---

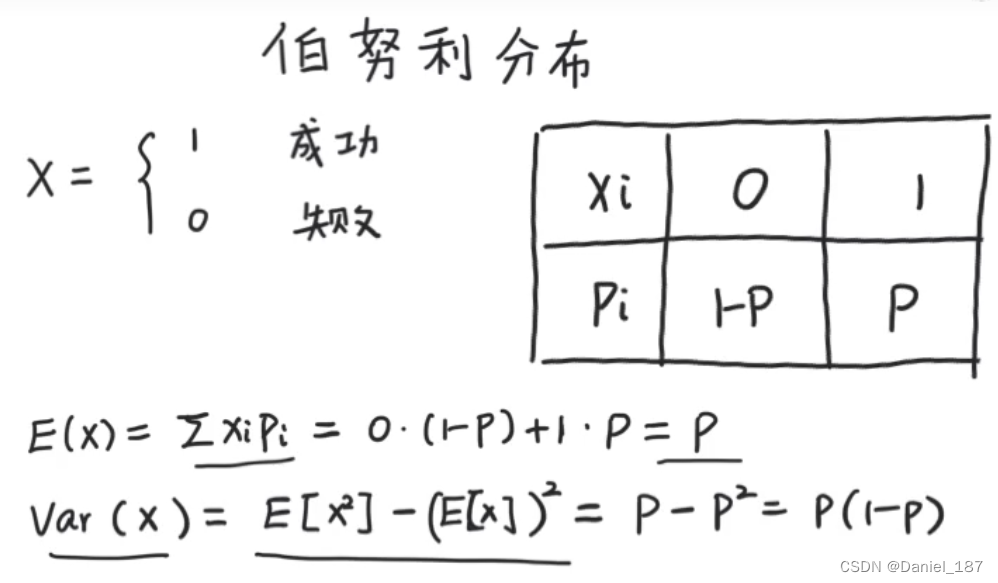
切比雪夫不等式

类似于正态分布的3$\sigma$原则，切比雪夫不等式在不限制数据分布的情况下，给出了数据分布的一个保守估计：
P { ∣ X − E ( X ) ∣ ≥ ε } ≤ D ( X ) ε 2 P\{|X-E(X)|\ge \varepsilon\}\le \frac{D(X)}{\varepsilon^2} P{∣X−E(X)∣≥ε}≤ε2D(X)​

或

P { ∣ X − E ( X ) ∣ ≤ ε } ≥ 1 − D ( X ) ε 2 P\{|X-E(X)|\le \varepsilon\}\ge 1-\frac{D(X)}{\varepsilon^2} P{∣X−E(X)∣≤ε}≥1−ε2D(X)​

其中$D(X)={\sigma }^2$，通常$\epsilon$取$\sigma$的整数倍，代表了随机变量距离均值中心有几个方差。

---

最大似然估计

核心思想：未知参数取何值时，样本的观测值出现的概率最大

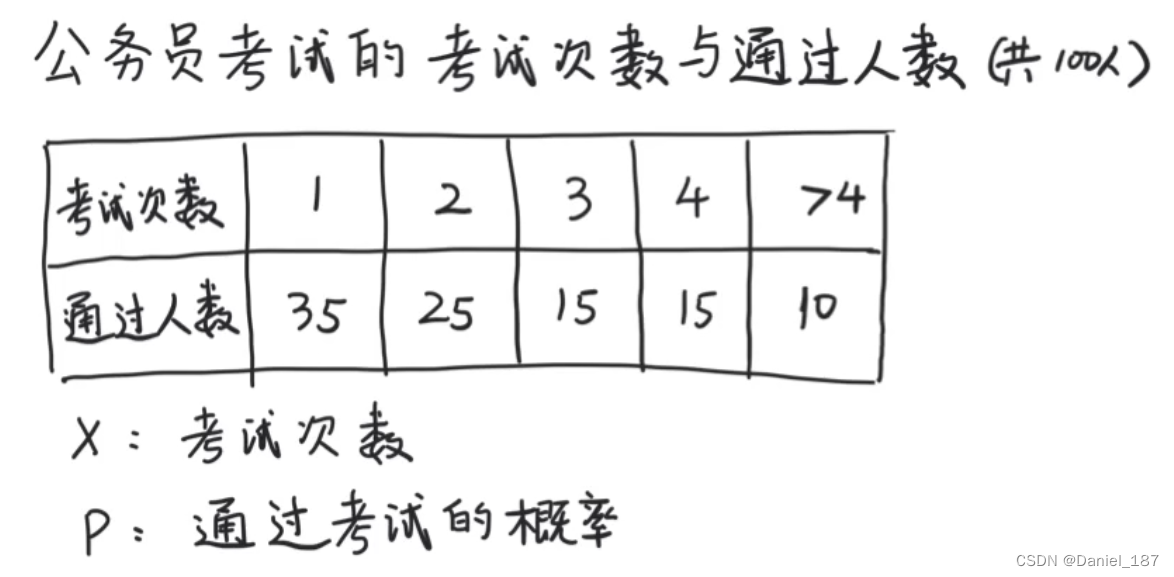
求考试的通过率$p$

X服从几何分布：$P(X=n)=(1-p{)}^{n-1}p$

构造最大似然函数：

$$L(p)=L(x_1,x_2,...x_{100};p)=P(x_1,x_2,...x_{100})$$

带入数值得：

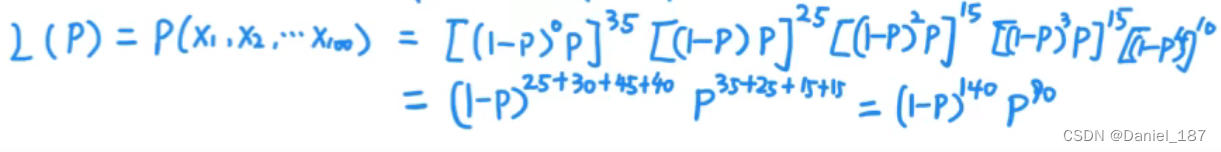
取对数求极值，得到p $\approx$ 0.39

---