LeetCode：二叉树的最大深度

1、题目描述

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

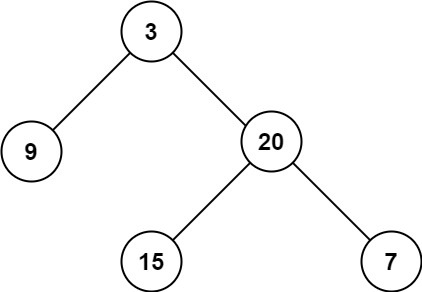
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。

• -100 <= Node.val <= 100

2、方法：递归法（深度优先DFS）

解题思路

递归法通过分解问题为子问题求解，分别计算左右子树的最大深度，再取较大值加 1（当前节点）。

步骤：

1. 终止条件：当前节点为 null 时，深度为 0。

2. 递归计算：

   • 计算左子树的最大深度 leftDepth。

   • 计算右子树的最大深度 rightDepth。

3. 返回结果：max(leftDepth, rightDepth) + 1。

时间复杂度：O(n)，空间复杂度：O(n) （调用栈）

public int maxDepth(TreeNode root) {
    if (root == null) return 0;  // 终止条件
    int leftDepth = maxDepth(root.left);   // 递归左子树
    int rightDepth = maxDepth(root.right); // 递归右子树
    return Math.max(leftDepth, rightDepth) + 1; // 当前节点深度
}

3、方法2：迭代法（广度优先BFS）

解题思路

迭代法通过队列按层遍历节点，每遍历完一层，深度加 1。

步骤：

1. 初始化：根节点入队，初始化深度 depth = 0。

2. 按层遍历：

   • 记录当前层的节点数 size。

   • 弹出 size 个节点，并将它们的子节点入队。

   • 每处理完一层，depth++。

3. 返回结果：队列为空时返回 depth。

时间复杂度：O(n)，空间复杂度：O(n) （栈空间）

public int maxDepth(TreeNode root) {
    if (root == null) return 0;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    int depth = 0;
    while (!queue.isEmpty()) {
        int size = queue.size();  // 当前层的节点数
        while (size-- > 0) {      // 处理当前层所有节点
            TreeNode currNode = queue.poll();
            if (currNode.left != null) queue.offer(currNode.left);
            if (currNode.right != null) queue.offer(currNode.right);
        }
        depth++;  // 层数增加
    }
    return depth;
}