POJ 3070 Fibonacci 【矩阵快速幂取模（模板）】_acm fibonacci 快速幂取模-优快云博客

本文介绍了一种利用矩阵快速幂取模的方法来高效计算斐波那契数列的大数值问题，并提供了一个具体的AC代码实现示例。

Fibonacci

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 13262		Accepted: 9430

Description

In the Fibonacci integer sequence, F₀ = 0, F₁ = 1, and F_n = F_n_{− 1} + F_n_{− 2} for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

Given an integer n, your goal is to compute the last 4 digits of F_n.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of F_n. If the last four digits of F_n are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print F_n mod 10000).

Sample Input

Sample Output

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

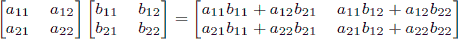Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

题意：用矩阵快速幂取模求斐波拉契的项；

思路：直接上模板就行，在相乘的过程中进行取模运算；

失误：矩阵快速幂的代码有点麻烦，尽量写的简化一点；

AC代码：

#include<cstdio>
#include<cstring>

typedef long long LL;
const LL MOD=10000;

struct Matrix{
	LL Mat[3][3];
};

Matrix ori,res;

Matrix Mat_mul(Matrix X,Matrix Y)
{
	Matrix Z; memset(Z.Mat,0,sizeof(Z.Mat));
	LL i=0,j=0,k=0;
	for(i=1;i<=2;++i)
	{
		for(k=1;k<=2;++k)
		{
			if(X.Mat[i][k]==0) continue;
			for(j=1;j<=2;++j)
			{
				Z.Mat[i][j]+=(X.Mat[i][k]*Y.Mat[k][j])%MOD;
				Z.Mat[i][j]%=MOD;
			}
		}
	}
	return Z; 
}

void Mat_Q(LL M)
{  
    ori.Mat[1][1]=1; ori.Mat[1][2]=1; 
    ori.Mat[2][1]=1; ori.Mat[2][2]=0;
    res.Mat[1][1]=res.Mat[2][2]=1;
	res.Mat[1][2]=res.Mat[2][1]=0;
	    
	while(M)
	{
		if(M&1) res=Mat_mul(res,ori);
		ori=Mat_mul(ori,ori);
		M>>=1;
	}
}
int main()
{
	LL N;
	while(~scanf("%lld",&N),~N)
	{	
	    if(N==0) printf("0\n");
		else if(N==1) printf("1\n");
		else {
	         Mat_Q(N-1);
			 printf("%lld\n",res.Mat[1][1]);		 
		}    
	} 
	return 0;
 }