四 分类：基本概念，决策树与模型评估1

4.1预备知识

元组（x，y）：x指属性集合，y指分类属性

目标函数又称为分类模型：描述性建模；预测性建模

4.2 解决分类问题的一般方法

分类技术是一种根据输入数据集建立分类模型的系统方法。
学习算法确定分类模型；泛化能力模型
训练集；检验集

分类模型性能评估：
1.正确错误计数（混淆矩阵）

2.错误率，正确率

4.3 决策树归纳

4.3.1 决策树的工作原理

决策树：根结点，内部结点（属性测试条件），叶结点（类标号）

4.3.2 如何建立决策树

属性集太大，决策树高度指数级，局部最优决策构造具有一定准确率的次优决策树
1.Hunt算法：（基本思想：已经确定了类别的结点不用继续分解下去）

2.决策树归纳的设计问题
如何分裂训练记录；如何停止分类过程

4.3.3 表示属性测试条件的方法

二元属性：二元划分
标称属性：二元划分或多路划分
序数属性：二元划分或多路划分，不能违背有序性
连续属性：测试条件选择比较测试二元输出；离散化策略

4.3.4 选择最佳划分的度量

选择最佳划分的度量通常是根据划分后子女结点不纯性的程度。不纯性度量方法：

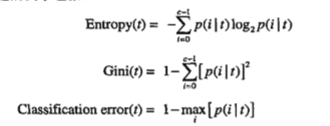
为确定测试条件的效果，需比较父节点和子女结点的不纯程度。差越大，测试条件越好。
增益：

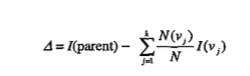
决策树归纳采用最大化增益的测试条件，即最小化子女结点的不纯性度量的加权平均。
当选择熵作为不纯度量时，熵的差就是信息增益。
1.二元属性的划分
2.标量属性的划分
3.连续属性的划分
4.增益率：决策树算法C4.5

4.3.5 决策树归纳算法

4.3.6 例子:Web机器人检测（反爬虫）

4.3.7 决策树归纳的特点

1.构建分类模型的非参数方法
2.NP完全问题
3.计算代价小
4.决策树容易解释
5.学习离散值
6.避免过分拟合
7.冗余数据不会造成影响
8.叶结点记录少，不具统计意义：数据碎片问题设置阈值
9.子树重复问题
10.测试条件只涉及一个属性：斜决策树
11.不纯度量方法影响小