统计学习笔记6—逻辑斯谛回归与最大熵模型

第六章 逻辑斯谛回归与最大熵模型

6.1 逻辑斯谛回归模型

6.1.1 逻辑斯谛分布

6.1.2 二项逻辑斯谛回归模型

模型定义：

将b加入到内积中：

几率定义：该事件发生的概率与不发生的概率的比值。
则逻辑斯谛回归的几率为：

6.1.3 模型参数估计

模型参数w估计：极大似然估计
求解过程：

6.1.4 多项逻辑斯谛回归

6.2 最大熵模型

6.2.1最大熵原理

鸡蛋篮子原理：在信息未知的条件下，等可能概率，即熵最大。

6.2.2 最大熵模型的定义

特征函数的经验分布期望和模型的期望相等，即为约束条件：

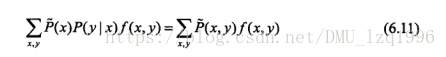
在满足约束条件下，求解熵最大称为熵最大模型：

参考笔记：https://blog.youkuaiyun.com/itplus/article/details/26550201

6.2.3 最大熵模型的学习

学习过程形式化为约束最优化问题，即：

求解过程：拉格朗日数乘法
求解结果：对偶函数的极大化
详细过程参考课本。

6.2.4 极大似然估计

对偶函数的极大化等价于最大熵模型的极大似然估计。
so，最大熵模型的学习问题转化为具体求解对数似然函数极大化问题。

6.3 模型学习的最优化算法

逻辑斯谛回归模型和最大熵模型学习归结为似然函数为目标函数的最优化问题。

6.3.1 改进的迭代尺度法IIS（最大熵模型学习的最优化算法）

6.3.2拟牛顿法BFGS算法