知识准备
极大似然估计
极大似然估计就是给定一个训练数据集T, 寻找模型的最优参数值θ, 达到一个这样的效果: 给模型输入训练集的X, 能以最大的概率输出其正确的分类Y. 求θ的过程就是最大化似然函数L(θ)的过程.
L(θ)=P(T|θ)=P(x1,...,xN|θ)=∏i=1NP(xi|θ)L(θ)=P(T|θ)=P(x1,...,xN|θ)=∏i=1NP(xi|θ) , 式中P(T|θ)是联合概率分布(训练集的样本都是独立同分布的).
求解方式: 一阶导数为0.
∑i=1N∇θlnP(xi|θ)=0∑i=1N∇θlnP(xi|θ)=0 , 该方程的解只是个估计值, 只有样本数目趋于无限多时, 它才接近真实值.
1. 逻辑斯谛回归模型
逻辑斯谛回归 = logistic regression
1.1 逻辑斯谛分布
定义: X是连续随机变量, 如果X满足下列的分布函数和密度函数, 则X服从逻辑斯谛分布
F(x)=P(X≤x)=11+e−(x−μ)/γF(x)=P(X≤x)=11+e−(x−μ)/γ
f(x)=F′(x)=e−(x−μ)/γ1+eγ((x−μ)/γ)2f(x)=F′(x)=e−(x−μ)/γ1+eγ((x−μ)/γ)2
(μ为位置参数, γ为形状参数)
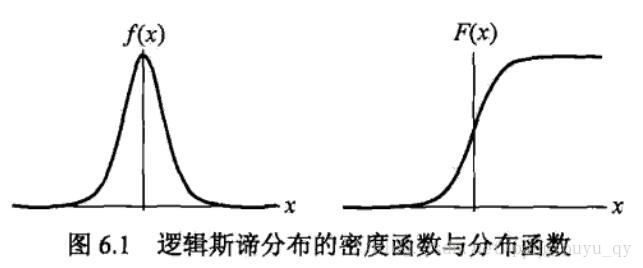
γ越小, F(x)中间增长的那一段就越陡.
1.2 二项逻辑斯谛回归模型
该模型是一种分类模型. 由条件概率P(Y|X)表示, X为实数, Y为0或1.
定义: 该模型是如下的条件概率分布.
P(Y=1|x)=exp(w⋅x+b)1+exp(w⋅x+b)P(Y=1|x)=exp(w·x+b)1+exp(w·x+b)
P(Y=0|x)=11+exp(w⋅x+b)P(Y=0|x)=11+exp(w·x+b)
w和b也可以写在一起
P(Y=1|x)=exp(w⋅x)1+exp(w⋅x)P(Y=1|x)=exp(w·x)1+exp(w·x)
P(Y=0|x)=11+exp(w⋅x)P(Y=0|x)=11+exp(w·x)
比较两个条件概率的大小, 将实例x分到概率值较大的那一类.
1.3 模型参数估计
可以应用极大似然估计法估计模型参数.
设: P(Y=1|x) = π(x), P(Y=0|x) = 1-π(x).
似然函数为: ∏i=1N[π(xi)]yi[1−π(xi)]1−yi∏i=1N[π(xi)]yi[1−π(xi)]1−yi
对数似然函数为: L(w)=∑i=1N[yi(w⋅xi)−log(1+exp(w⋅xi)]L(w)=∑i=1N[yi(w·xi)−log(1+exp(w·xi)]
参数(w)估计即为以对数似然函数为目标函数的最优化问题. 可以采用梯度下降法及牛顿法.
1.4 多项逻辑斯谛回归
多项逻辑斯谛回归模型可以表示为如下的形式:
P(Y=k|x)=exp(wk⋅x)1+∑k=1K−1exp(wk⋅x)P(Y=k|x)=exp(wk·x)1+∑k=1K−1exp(wk·x) , k=1,2,...,K−1k=1,2,...,K−1
P(Y=K|x)=11+∑k=1K−1exp(wk⋅x)P(Y=K|x)=11+∑k=1K−1exp(wk·x)
2. 最大熵模型
2.1 最大熵原理
原理表述: 在满足约束条件的模型集合中选取熵最大的模型.
设离散随机变量X的概率分布P(X), 则其熵为
H(P)=∑xP(x)logP(x)H(P)=∑xP(x)logP(x)
熵满足如下不等式: (|X|是X的取值个数)
0≤H(P)≤log|X|0≤H(P)≤log|X|
当且仅当X的分布是均匀分布时右边的等号成立, 即均匀分布的熵最大.
对最大熵原理的理解: 模型首先要满足约束条件(已有的事实), 在约束条件之外通常有不确定的部分, 对于这些部分, 我们认为他们是等可能的. Eg. X有四个取值{A, B, C, D}, 约束条件有2个:
P(A) + P(B) + P(C) +P(D) = 1
P(A) + P(B) = 0.4
我们用最大熵原理对X的概率分布进行估计的结果为: P(A) = P(B) = 0.2, P(C) = P(D) = 0.3
2.2 最大熵模型的定义
假设分类模型是一个条件概率分布P(Y|X).
给定训练集可以确定联合分布P(X,Y)的经验分布和边缘分布P(X)的经验分布, 分别以P^(X,Y)P^(X,Y)和P^(X)P^(X)来表示:
P^(X=x,Y=y)=v(X=x,Y=y)NP^(X=x,Y=y)=v(X=x,Y=y)N
P^(X=x)=v(X=x)NP^(X=x)=v(X=x)N
定义一个特征函数f(x,y)描述输入x和输出y之间的某个事实:
f(x,y)={1,0,x与y满足某一事实否则f(x,y)={1,x与y满足某一事实0,否则
特征函数关于经验分布P~(X,Y)P~(X,Y)的期望值为:
EP~(f)=∑x,yP~(x,y)f(x,y)EP~(f)=∑x,yP~(x,y)f(x,y)
特征函数关于模型P(Y|X)与经验分布P^(X)P^(X)的期望值为:
EP(f)=∑x,yP^(x)P(y|x)f(x,y)EP(f)=∑x,yP^(x)P(y|x)f(x,y)
如果模型能准确获取训练数据中的信息, 那么这两个期望应该是相等的.
∑x,yP~(x,y)f(x,y)=∑x,yP^(x)P(y|x)f(x,y)∑x,yP~(x,y)f(x,y)=∑x,yP^(x)P(y|x)f(x,y)
上式即为模型的约束条件, 有n个特征函数就有n个约束条件. 满足此约束条件且条件熵H(P)最大的模型即为最大熵模型
H(P)=−∑x,yP^(x)P(y|x)logP(y|x)H(P)=−∑x,yP^(x)P(y|x)logP(y|x)
2.3 最大熵模型的学习
最大熵模型的学习等价于约束最优化问题:
约束条件为: EP(fi)−EP^(fi)=0EP(fi)−EP^(fi)=0 且 ∑yP(y|x)=1∑yP(y|x)=1
最优化的目标为: minP∈C−H(p)=∑x,yP^(x)P(y|x)logP(y|x)minP∈C−H(p)=∑x,yP^(x)P(y|x)logP(y|x)
推导过程略(利用了拉格朗日函数)
推导结果(归结为求对偶函数的极大化)
2.4 极大似然估计
对偶函数的极大化等价于最大熵模型的极大似然估计.(证明略)
3. 模型学习的最优化算法
逻辑斯谛回归模型, 最大熵模型学习归结为以似然函数为目标函数的最优化问题, 求解方式通常为迭代算法. 此节提出更优化的算法.





 本文介绍极大似然估计的基本概念及其在逻辑斯谛回归和最大熵模型中的应用,并探讨了模型学习的最优化算法。
本文介绍极大似然估计的基本概念及其在逻辑斯谛回归和最大熵模型中的应用,并探讨了模型学习的最优化算法。
















 399
399

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








