人工智能之图像识别----卷积网络

卷积网络

卷积网络，也叫做卷积神经网络，是一种专门用来处理具有类似网络结构的数据的神经网络，例如时间序列数据（认为是在时间轴上有规律的采样形成的一维网络）和图像数据（可以看作二维的像素网络）。

理论教学环节

卷积运算

定义：我们称(f *g)(n)是 f，g的卷积
其连续的定义是(f *g)(n) = ${\int }_{-\infty }^{\infty }$f(t) g(n-t) dt
其离散的定义是(f *g)(n) = ${\sum }_{t=-\infty }^{\infty }$f(t) g(n-t)
这两个式子有一个共同特征：

那么又有什么规律呢？
如果我们令x = t, y = (n-t)，那么我们就可以得到x+y = n这条直线

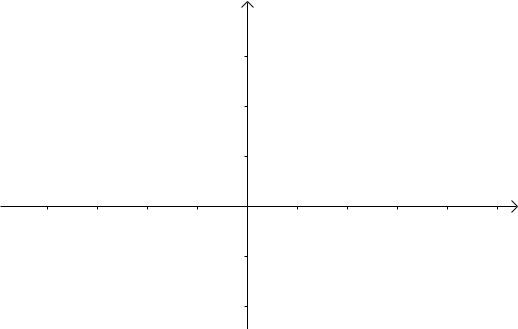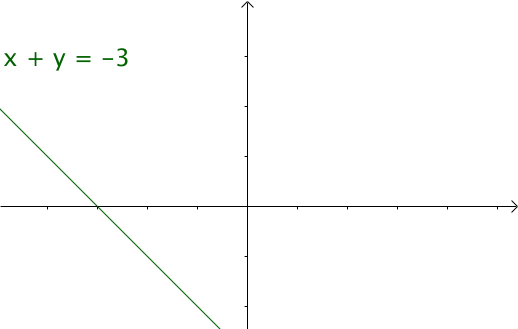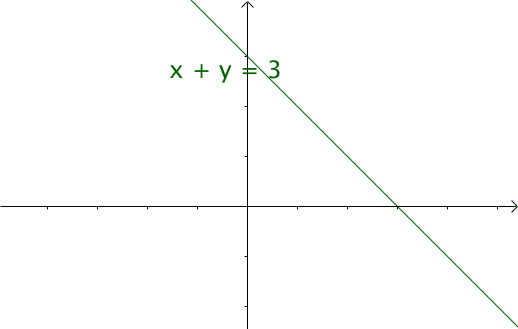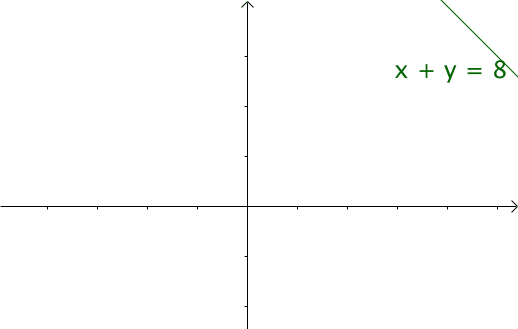
如果遍历这条直线，那么就像卷毛巾一样沿着角卷起来，这样卷出来的毛巾在将毛巾铺平后留下的卷痕的直线都是满足这个方程的。

而卷积的过程即可以看成是在卷毛巾，而结果则是卷毛巾的过程中根据毛巾的长宽范围内卷出来的面积

而在神经网络中，我们会用一个相关的函数，称为互相关函数
如下将会展示一个二维卷积的例子：
如图的二维输入的大小是3*4，而卷积核（wxyz）则为2*2的，卷积核则是卷积过程中的第二个参数，也就是上面所讲的g（n-t），我们只对核完全处在图像中的位置进行输出，于是就会按照卷积核的大小在输入上进行移动计算，从左到右，从上到下，得出如输出所示的六个值

卷积运算的动机

卷积运算通过三个重要的思想来优化改进机器学习系统：稀疏交互、参数共享、等变表示

稀疏交互

传统的神经网络通过矩阵乘法来建立输入与输出的连接关系，其中参数矩阵的每一个参数都描述了一个输入单元和一个输出单元的交互，这使得连接的效率大大降低。而卷积网络采用的稀疏交互的特征，使核的大小远远小于输入的大小，这意味着我们可以用更少的存储参数来保存更多有意义的边缘参数，不仅减少了存储需求，还提高了统计效率，例如卷积核为3*3的方式，下图的x为输入层，s为输出层：

其中上面的为稀疏交互，可以看到，每一个输入最多对应了三个输出，而对于下面的矩阵乘法的方式，每一个输入都对应了所有的输出，使得运算量与复杂程度远远大于稀疏交互的方式

参数共享

参数共享指的是一个模型的多个函数使用相同的参数，同样的，在矩阵乘法的方式中，每一个输出函数都将所有的输入参数对应起来，此时任何一个参数改变都会影响输出结果；而在卷积网络中，每一个函数对应最多只有卷积核的宽度个参数，在这里最多只有三个参数会影响最终结果的输出，这使得存储需求和统计效率方面极大的优于稠密矩阵的乘法运算，下图展示了参数共享的实现过程：

那么可能有同学就要问了，“如果我想对应起所有的参数怎么办呢”
对应的，我们可以使输出函数层处于神经网络中更深层的位置，因为处于更深的层中的单元的接受域是比浅层的单元的接受域更大的，所以尽管在卷积网络中是稀疏连接的，处于更深层的单元依然可以间接的连接到全部或大部分输入内容，过程如下：

等变表示

等变表示可以理解成当输入产生变化时，其结果也会产生相同的变化，例如将图片的输入像素向右调整一位，那么卷积之后表示出来的结果也必然会以同样的方式向右移动一位

好的，我们大致知道卷积运算是个什么东西之后，那么我们要怎么用它呢

实战教学环节

首先我们需要安装mxnet，用python 的pip安装即可：

	pip install mxnet

首先，卷积窗口肯定是从左到右，从上到下的顺序，依次在输入数组滑动的，滑动到某一位置时，窗口中的输入子数组与核数组按元素相乘求和，得出输出数组中对应位置的元素，所以可以由图分别得到：

00+11+32+43 = 19
10+21+42+53 = 25
30+41+62+73 = 37
40+51+72+83 = 43

综上所述我们可以写一个函数实现

from mxnet import nd
#二维互相关运算,X为输入数组，k为卷积核
def corr2d(X,k):
	#h为卷积核的高height，w为卷积核的宽width
    h,w = k.shape
    #Y为输出数组，其中输出数组的高为 输入数组的高-卷积核的高+1， 输出数组的宽为输入数组的宽-卷积核的宽+1
    Y = nd.zeros((X.shape[0]-h+1,X.shape[1]-w+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
        	#对输入数组中的高为i~i+h，宽为j~j+w的子数组进行卷积运算
            Y[i,j] = (X[i:i+h,j:j+w]*k).sum()
    return Y

于是我们就可以根据这个函数进行实验

X = nd.array([[0,1,2],[3,4,5],[6,7,8]])
k = nd.array([[0,1],[2,3]])
corr2d(X,k)

得出如下结果，与原图结果相同

[[19. 25.]
 [37. 43.]]
<NDArray 2x2 @cpu(0)>

填充和步幅

填充

就像上面那样，我们输出的数组与输入的数组的大小是不一样的，那么如果我们需要使他们大小一样那该咋办呢？这时候就需要用上填充的方法啦
填充是指在输入高和宽的两侧填充元素（通常是0元素）
如果我们在上面那个图所示的上方和左方填充一排0，那么我们就会得到下图所示

最终结果也将被填充成输入的3*3的样式，那么填充有什么规律呢？

一般来说，假设输入形状是n_h x n_w，卷积核窗口形状是k_h x k_w，在高的两侧一共填充p_h行，在宽的两侧一共填充p_w列，那么输出的形状则是：
(n_h - k_h + p_h+1) x (n_w - k_w + p_w + 1)

我们来一个例子解释一下:

from mxnet import nd
from mxnet.gluon import nn

#这边用到了一个nn里边创建卷积计算的方法Conv2D,不是上边自己创建的那个,其中大小是(5,3)的核
conv2d = nn.Conv2D(1,kernel_size = (5,3))
#conv2d = nn.Conv2D(1,kernel_size = (5,3),padding = (2,1))
#初始化conv2d
conv2d.initialize()
'''
#填充的时候使用的是padding,若带有两个参数则分别是高和宽,若带有一个参数则是四周
#其中高和宽都是两边添加参数位数行或列的值,比如(8,8)的数组padding为(2,1)则会变成(12,10)再进行卷积
'''

#创建一个8*8的数组,然后把参数默认设置成(1,1)
#因为再Conv2D(X)里参数X需要一个四维的数组,前面两个分别是批量和通道,我们下次再讲
X = nd.random.uniform(shape = (8,8))
X = X.reshape((1,1) + X.shape)
#处理完之后X应该是(1,1,8,8)

Y = conv2d(X)
Y.shape
#输出为(1,1,4,6),只需要关心后面两位,前面的是批量和通道,4 = 8 - 5 + 1, 6 = 8 - 3 + 1
#添加padding后输出为(1,1,8,8),高8 = 8 + 2*2 - 5 + 1, 宽8 = 8 + 1*2 - 3 + 1

步幅

有了填充来增加输出的数组大小，那么对应的也有用来减小输出的数组大小的方法,称为步幅
在之前的例子里,我们采取的步幅都为1，所以每次卷积核只会往下一步移动一格，当我们的步幅变为2时，每一次移动就会移动两格，使输出的大小减半，那么我们同样来探寻规律

一般来说，假设输入形状是n_h x n_w，卷积核窗口形状是k_h x k_w，在高的两侧一共填充p_h行，在宽的两侧一共填充p_w列，高上步幅为s_h，宽上步幅为s_w,那么输出的形状则是：
[(n_h - k_h + p_h+s_h)/s_h] x [(n_w - k_w + p_w + s_w)/s_w]

那么我们以实验带过，承上启下，我们还用之前的那一套，但是我们在conv2d初始化那块再加一个步幅strides

conv2d = nn.Conv2D(1,kernel_size = (5,3),padding = (2,1),strides = 2)
#然后其他原样输出，结果就改变了
#结果变成（1，1，4，4）

至此，卷积网络的简单理解介绍完毕