数据线性拟合优化之路

最近接到一个问题：

线性拟合是怎么实现的
线性拟合怎么优化

当时一时兴起的我就马上跑去百度谷歌了一番，发现似乎并没有想象的这么简单，于是先简单总结一下：

线性拟合是什么？

线性拟合是曲线拟合的一种形式。设x和y都是被观测的量，且y是x的函数：y=f(x; b)，曲线拟合就是通过x,y的观测值来寻求参数b的最佳估计值，及寻求最佳的理论曲线y=f(x; b)。当函数y=f(x; b)为关于b的i线性函数时，称这种曲线拟合为线性拟合。（摘自百度百科）

说白了，就是将一堆包含x，y值的坐标点放在一个二维平面，然后用尽可能接近每个点的一条曲线去描述它，鉴于问题太多，我这里就先讲讲直线的拟合叭

作为一组数据（x，y各一组应该是两组才对），应该有自己的想法，自己上二维数组的画板才对了呀（python可以用matplotlib.pyplot里的方法简易实现）

好的那么它上去了，我们继续。

线性拟合怎么实现？

这是个好问题，我们想将数据拟合成一条直线，如果是用纸笔我们会怎么做呢
“哎，这么简单，不就是用尺子量到差不多然后画一笔就好了嘛”
“像这样是吧，那我要怎么判断这条线是不是拟合的线呢？”

“你看一哈子不就好咯”

好啦，言归正传，要将这个直线画出来呢，我们都知道一条直线可以用方程表述出来，也就是y = kx + b；其中呢，k 为直线的斜率，b 就是这条直线的 y 截距啦（没别的，就y = kx + b）

最小二乘法

作为一条直线，最重要的就是斜率和截距，作为一个耿直boy，那就直一点，直接将直线的斜率和截距求出来，这时候我们就用到了最小二乘法，而它是干嘛的呢：

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。（摘自百度百科）

简单的说，就是求点到直线的垂直距离，根据横坐标来计算点到直线上垂直距离的差值。对这个点的值和拟合直线的距离求和，然后分别对k和b求导的方法来算出k和b的值。具体的求解过程可以看另一篇文章：

文章链接，还没有写，写后修改

距离图就如下啦

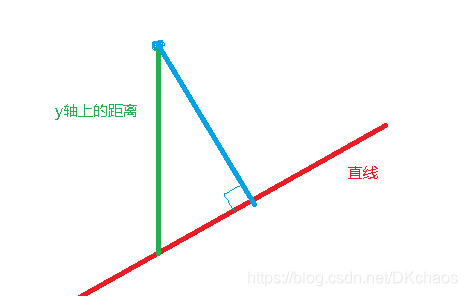
#python代码如下：传入x和y两个数组，就会通过求平方和的方式得出结果，b,k的算法原理我会写在最小二乘法的原理上
def linefit(x,y):
    N=int(len(x))
    sumx,sumy,sumx2,sumxy=0,0,0,0
    for i in range(0,N): 
        sumx+=x[i]
        sumy+=y[i]
        sumx2+=x[i]**2
        sumxy+=x[i]*y[i]
    b=(sumy*sumx2-sumx*sumxy)/(N*sumx2-sumx**