QAM映射中功率归一化因子的理解

2011-03-08

转自http://www.dsplog.com/2007/09/23/scaling-factor-in-qam/

 

When QAM (Quadrature Amplitude Modulation) is used, typically one may find a scaling factor associated with the constellation mapping operation. It may be reasonably obvious that this scaling factor is for normalizing the average energy to one.

This post attempts to compute the average energy of the 16-QAM, 64-QAM and M-QAM constellation (where  is a power of 2), thanks to the nice example 5.16 in [DIG-COMM-BARRY-LEE-MESSERSCHMITT].

Consider a typical 16-QAM modulation scheme where the alphabets

 are used.

 

 

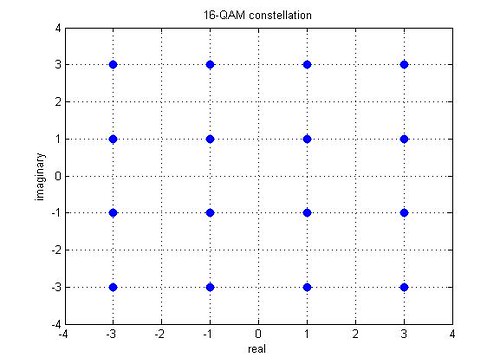
Figure: 16QAM constellation mapping

Observations:

1. The number/type of the used constellation points in all the four quadrants are similar. Hence average energy computed over one quadrant is same as the energy over all the quadrants. The mean power can be computed over 16/4 = 4 constellation points.

2. The same alphabet set is used for real and imaginary axis. Hence energy of real and imaginary components are the same.

3. In each quadrant, the elements of each alphabet is used  times by real and imaginary part respectively.

Considering so the average energy of 16-QAM is,

.

Hence the constellation points of 16-QAM are normalized with the factor  to ensure that the average energy over all symbols is one.

Consider a 64-QAM modulation scheme with the alphabets

 

 

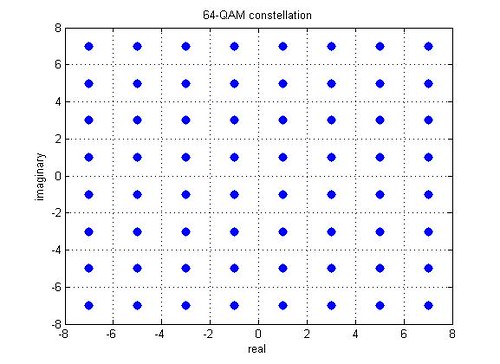
Figure: 64QAM constellation mapping

Observations for 64-QAM:

1. Each quadrant has 16 constellation points

2. The energy of real and imaginary components are the same.

3. In each quadrant, the elements of each alphabet is used  times by real and imaginary part respectively.

Hence the constellation points of 64-QAM are normalized with the factor  to ensure that the average energy over all symbols is one.

Extending this to a general M-QAM constellation mapping, where  is a power of 2. The elements of the alphabet are

, where .

1. Each quadrant has  constellation points

2. The energy of real and imaginary components are the same.

3. In each quadrant, the elements of each alphabet is used  times by real and imaginary part respectively.

.

% Simple Matlab example

% QAM scaling factor
clear
clc
alpha_16qam = [-3 -1 1 3];
N = 10^5;
const_16qam = randsrc(1,N,alpha_16qam) + j*randsrc(1,N,alpha_16qam); % generating 16-QAM constellation points
energy_16qam = const_16qam*const_16qam’/N

alpha_64qam = [-7 -5 -3 -1 1 3 5 7];
const_64qam = randsrc(1,N,alpha_64qam) + j*randsrc(1,N,alpha_64qam); % generating 16-QAM constellation points
energy_64qam = const_64qam*const_64qam’/N

Can observe that energy_16qam and energy_64qam takes values close to 10 and 42 respectively.

Hope this helps.

Krishna

Reference

[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt

Please click here to SUBSCRIBE to newsletter and download the FREE e-Book on probability of error in AWGN. Thanks for visiting! Happy learning.