二叉树_2(一文搞懂二叉树遍历)

3.1 二叉树的存储

        二叉树的存储结构分为： 顺序存储 和 类似于链表的链式存储 。

顺序存储在下节介绍。

        二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方式，具体如下：

// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}

3.2 二叉树的遍历

3.2.1遍历

        遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所作的操作依赖于具体的应用问题（比如：打印结点内容，结点内容+1）。遍历是二叉树最重要的操作之一，是二叉树上进行其他运算的基础。

3.2.2 前 中 后 序遍历

        如果用N代表根结点，L代表根结点的左子树，R代表根结点的右子树，则根据根结点的先后次序有以下遍历方式：

        NLR：前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树（根左右）。

        LNR：中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树（左根右）。

        LRN：后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点（左右根）。

        三种遍历的图解：        由上图可知：树是递归定义的，每一棵树的遍历 都是以同样的方式进行遍历的，前 中 后 序遍历走的路线的相同的，不过是访问根结点的顺序不同。         

       下面我们先通过一道题来认识这三种遍历：请写出以下二叉树的3种遍历方式：

        前序遍历：A B D E H C F G

        中序遍历：D B E H A F C G

        后序遍历：D H E B F G C A

 3.2.3 层序遍历

         层序遍历就是从二叉树的根出发，从上到下，自左至右的逐层逐个访问树的结点。

 3.2.4 选择题

1.某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为(  )   

A: ABDHECFG   B: ABCDEFGH   C: HDBEAFCG   D: HDEBFGCA  

        依题意，可画出图如下： 

        前序遍历是根左右，所以结果是：ABDHECFG，选择：A。 

2. 二叉树的先序遍历和中序遍历如下：先序遍历： EFHIGJK; 中序遍历： HFIEJKG. 则二叉树根结点为 (  )

A: E     B: F     C: G     D: H

        因为先序遍历的第一个就是根节点，所以答案是：A。那么，下面对这道题进行一个变形：

二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树后序遍历的顺序为： 

        因为先序遍历（根左右） ：E F H I G J K,中序遍历（左根右）：H F I E J K G,根据上面根节点为E，在E的左边的是左子树的节点，在E的右边的是右子树的节点：

        接下来我们可以通过先序遍历确定节点出现的顺序，通过中序遍历确定它是左节点还是右节点 ：可以看到在先序遍历中E后出现的是F，中序遍历中F在E的左边，所以F为E的左节点；后面出现的是H和I，H在F的左边，所以H是F左子树，而I在F的右边，所以I是F的右子树。

        接下来处理J、K、G，由先序遍历可知出现的顺序是G、J、K，又由中序遍历J是G的左节点，K是J的右节点。画出图如下：

        由图，可得后序遍历： H I F K J G E .

  3.设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为()

A: adbce       B: decab       C: debac       D: abcde

        上题我们讲到通过先序遍历判断节点出现的先后顺序，通过中序遍历判断左右节点。那么在这一题上就变成了：通过后序遍历判断节点出现的先后顺序，通过中序遍历判断左右节点，这里因为是后序遍历（左右根），所以出现的顺序是逆序出现，也就是说a是我们的根节点。又由中序遍历：b属于a的左子树，d、c、e属于a的右子树，先处理右子树：出现的顺序是c、e、d，e是c的右孩子，d是c的左孩子，最后，a左子树只有一个节点b。

        易得前序遍历abcde，选择A选项。 

4.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出(同一层从左到右)的序列为()

A: FEDCBA     B: CBAFED     C: DEFCBA     D: ABCDE

        后序遍历最后一个结点是F，F为根结点，中序遍历中 A B C D E均在F左侧，为F的左子树 

        易得二叉树如图：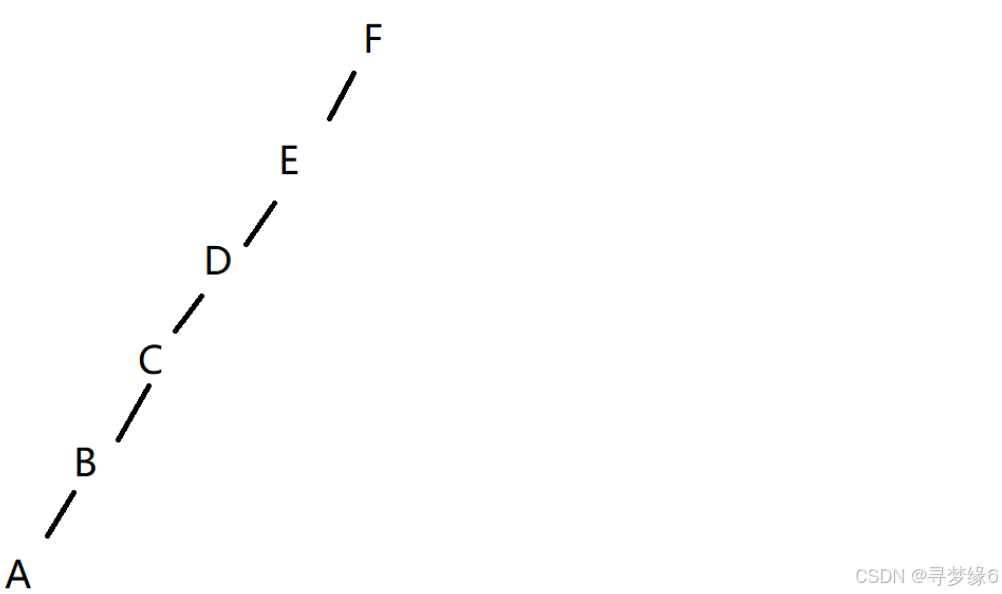

        层次序列为：F E D C B A ，选择A选项。

3.3 二叉树遍历的代码实现

        上文我们提到二叉树是通过递归定义的，下面我们通过递归来实现二叉树的遍历：

3.3.1 前序遍历

        前序遍历：是先输出根节点的值，然后递归左边，最后递归右边的一种遍历，注意这里的出递归的条件是当（root == null）时返回。

   public void preOrder(TreeNode root){
        if(root == null) return;    //出递归的条件
        System.out.print(root.val + " ");
        preOrder(root.left);//递归左边
        preOrder(root.right);//递归右边
    }

        我们也可以将前序遍历的结果存储到线性表中： 由于这是一棵字符树，所以返回一个字符型的顺序表。

public List<Character> preOrder3(TreeNode root){
        //创建线性表
        List<Character> ret = new ArrayList<>();
        //递归出口    
        if(root == null) return ret;
        //添加根
        ret.add(root.val);
        List<Character> leftTree = preOrder3(root.left);
        //添加左树        因为这里返回值是一个线性表所以需要使用addAll（）
        ret.addAll(leftTree);
        List<Character> rightTree = preOrder3(root.right);
         //添加右树 
        ret.addAll(rightTree);
        return ret;
    }

 3.3.2 中序遍历

    public void inOrder(TreeNode root){
        if(root == null) return;
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    }

    public List<Character> inorderTraversal(TreeNode root) {
        List<Character> ret = new ArrayList();
        if(root == null) return ret;
        List<Character> leftTree =  inorderTraversal(root.left);
        ret.addAll(leftTree);
        ret.add(root.val);
        List<Character> rightTree =  inorderTraversal(root.right);
        ret.addAll(rightTree);
        return ret;
    }

3.3.3 后序遍历 

    public void postOrder(TreeNode root){
        if(root == null) return;
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val + " ");
    }

 //后序遍历存储的是值
    public List<Character> postorderTraversal(TreeNode root) {
        List<Character> ret = new ArrayList();
        if(root == null) return ret;
        List<Character> leftTree = postorderTraversal(root.left);
        ret.addAll(leftTree);
        List<Character> rightTree = postorderTraversal(root.right);
        ret.addAll(rightTree);
        ret.add(root.val);
        return ret;
    }