二叉树 1-优快云博客

本文链接：https://blog.youkuaiyun.com/CxK6666667/article/details/146116708

1、树型结构

1.1 概念（了解）

树是一种非线性 的数据结构，它是由 n （ n>=0 ）个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看

起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的 。它具有以下的特点：

1、有一个特殊的节点，称为根节点，根节点没有前驱节点

2、除根节点外，其余节点被分成M(M > 0) 个互不相交的集合 T1 、 T2 、 ...... 、 Tm ，其中每一个集合 Ti (1 <= i <= m) 又是一棵与树类似的子树。每棵子树的根节点有且只有一个前驱，可以有 0 个或多个后继

3、树是递归定义的。

这是大自然中的一棵树：

这是数据结构的一棵树：

二者相比，可以看到数据结构的树就像是大自然中的树倒过来。注意：在树型结构中，子树之间不能有交集，否则就不是树型结构。

树与非树的判定：

1、子树是不相交的：如图1：孩子结点C与D间存在交集，所以不是树型结构。

2、除了根结点没有父节点外，每个节点有且仅有一个父节点：如图，每个结点有且仅有一个父节点。

3、一棵有N个结点的树有N - 1条边。（下面证明二叉树性质要用）如图3，有8个结点，应该有7条边，但图中有8条，则图3不是树型结构。

1.2 概念（重要）

结点的度 ：一个结点含有子树的个数称为该结点的度；如上图： A 的度为 6

树的度 ：一棵树中，所有结点度的最大值称为树的度；如上图：树的度为 6

叶子结点或终端结点 ：度为 0 的结点称为叶结点；如上图： B 、 C 、 H 、 I... 等节点为叶结点

双亲结点或父结点 ：若一个结点含有子结点，则这个结点称为其子结点的父结点；如上图：A是 B 的父结点。

孩子结点或子结点 ：一个结点含有的子树的根结点称为该结点的子结点；如上图： B 是 A 的孩子结点。

根结点 ：一棵树中，没有双亲结点的结点；如上图： A

结点的层次 ：从根开始定义起，根为第 1 层，根的子结点为第 2 层，以此类推。

树的高度或深度：树中结点的最大层次；如上图：树的高度为4

树的以下概念只需了解，在看书时只要知道是什么意思即可：

非终端结点或分支结点 ：度不为 0 的结点；如上图： D 、 E 、 F 、 G... 等节点为分支结点

兄弟结点 ：具有相同父结点的结点互称为兄弟结点；如上图： B 、 C 是兄弟结点

堂兄弟结点 ：双亲在同一层的结点互为堂兄弟；如上图： H 、 I 互为兄弟结点

结点的祖先 ：从根到该结点所经分支上的所有结点；如上图： A 是所有结点的祖先

子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是 A 的子孙

森林：由 m （ m>=0 ）棵互不相交的树组成的集合称为森林

1.3 树的表示形式（了解）

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式，如：双亲表示法，孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。代码：

classNode{
    int value;//树中存储的数据
    Node ﬁrstChild;//第一个孩子引用
    Node nextBrother;//下一个兄弟引用
}

1.4 树的应用

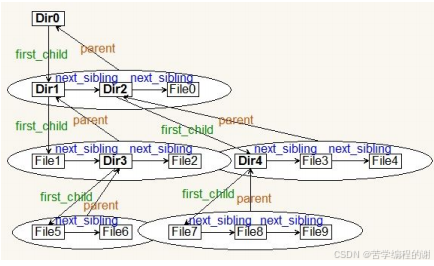
用于文件系统管理（目录和文件）

下图是linux系统模拟，windows系统的应用，就是打开我的电脑，不同盘下面的不同文件。

2、二叉树（重点！！！）

2.1 概念

一棵二叉树是结点的一个有限集合，该集合：

1. 或者为空

2. 或者是由一个根节点加上两棵别称为 左子树 和右子树的二叉树组成

由上图可以看出：

1. 二叉树不存在度大于 2 的结点

2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树（这里的有序并不是指大小有序而是逻辑上的左子树和右子树）。

注意：对于任意的二叉树都是由以下几种情况复合而成的：

2.2 两种特殊的二叉树

1. 满二叉树 : 一棵二叉树，如果 每层的结点数都达到最大值，则这棵二叉树就是满二叉树 。也就是说， 如果一棵满二叉树的层数为K，其 结点总数是2 ^ k - 1，则它就是满二叉树。

2. 完全二叉树：完全二叉树是效率很高的数据结构， 完全二叉树是由满二叉树引出的。 对于深度为K，有n个结点的二叉树，当且仅当其 每一个结点都与深度为K的满二叉树中编号从0至n - 1的结点一一对应时称之为完全二叉树。（这里的概念可能有些难理解：通俗易懂地说就是从上到下，从左到右依次排布结点地一棵树。） 注意：满二叉树是完全二叉树的一个特殊情况。

2.3 二叉树的性质（做题要用！！！）

1、若规定根结点的层数为1，则一棵非空二叉树的第 i 层上最多有 2 ^ (i - 1) (i > 0)个结点。（满二叉树）。

2、若规定只有根节点的二叉树的深度为1，则深度为K的二叉树的最大结点数是 2 ^ k -1 (k >= 0) （每个结点都存在2个左右孩子）。

3.对任意一棵二叉树，如果其叶结点（度为0的结点）的个数为n0，度为2的非叶结点个数为n2，则有 n0 = n2 + 1（翻译：对于任何一棵二叉树，叶子结点的个数永远比度为2的非叶子结点的个数多一个）。证明过程如下：

4. 具有 n 个结点的完全二叉树的深度 k 为向上取整

5.对于具有 n 个结点的完全二叉树，如果按照从上至下从左到右的顺序对所有结点从0开始编号，则对于序号为 i 的结点有（这个性质在优先级队列中要用到）：

5.1、已知父亲下标为 i 求孩子结点下标：左孩子：(2 * i) + 1 右孩子：(2 * i) + 2。

5.2、已知孩子下标 i 求父亲结点下标：(i - 1) / 2。

2.4 二叉树题目（性质相关）

1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为多少？

由性质3：叶子节点永远比度为2的节点多1个，所以一共有200个叶子节点。

2.在具有 2n 个结点的完全二叉树中，叶子结点个数为几？

因为二叉树有2n个节点，所以节点个数为偶数个，这里画图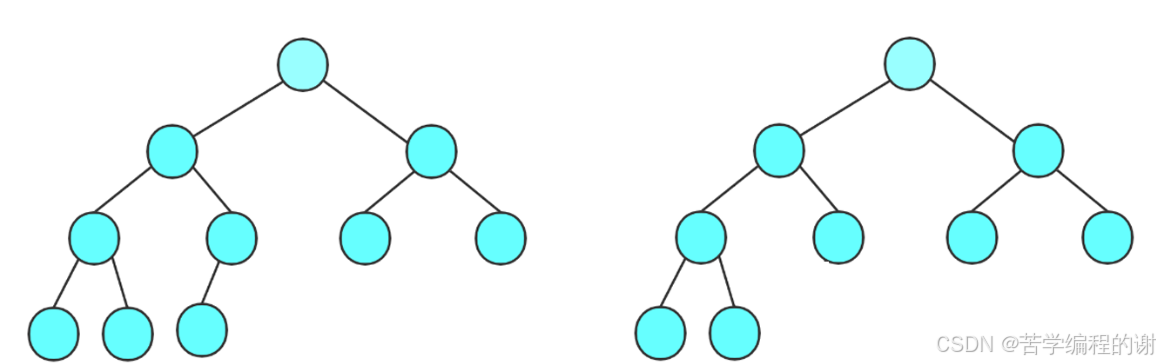：第一幅图的节点为偶数个，第二幅图节点为奇数个，我们知道一棵二叉树是由n0(度为0的节点)+n1(度为1的节点)+n2（度为2的节点构成）。由图可知：当节点为偶数个时，n1=1;当节点为奇数个时，n1=0。又根据n0 = n2+1,则有:2n = n0+n1+n2 = n0+1+n0-1,化简得：n0 = n。所以这里叶子节点个数为n。