LeetCode：2617. 网格图中最少访问的格子数（优先级队列 Java）

最新推荐文章于 2025-12-17 23:41:09 发布

原创最新推荐文章于 2025-12-17 23:41:09 发布 · 810 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #java #算法

文章讲述了如何利用优先级队列和动态规划方法解决网格图中从左上角到右下角的最少步数问题，通过维护行和列堆来确定可行路径并更新步数。

2617. 网格图中最少访问的格子数

题目描述：

给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。

当你在格子 (i, j) 的时候，你可以移动到以下格子之一：

满足 j < k <= grid[i][j] + j 的格子 (i, k) （向右移动），或者
满足 i < k <= grid[i][j] + i 的格子 (k, j) （向下移动）。

请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数，如果无法到达右下角格子，请你返回 -1 。

示例 1：

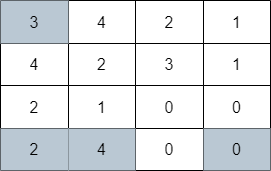
输入：grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]]
输出：4
解释：上图展示了到达右下角格子经过的 4 个格子。

示例 2：

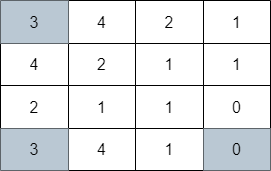
输入：grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]]
输出：3
解释：上图展示了到达右下角格子经过的 3 个格子。

示例 3：

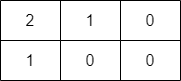
输入：grid = [[2,1,0],[1,0,0]]
输出：-1
解释：无法到达右下角格子。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 105
1 <= m * n <= 105
0 <= grid[i][j] < m * n
grid[m - 1][n - 1] == 0

实现代码与解析：

优先级队列

import java.util.Arrays;
import java.util.PriorityQueue;

class Solution {
    public int minimumVisitedCells(int[][] grid) {

        int n = grid.length, m = grid[0].length;
        int[][] d = new int[n][m]; // 到每个单元格的步数
        // 初始化
        for (int i = 0; i < n; i++) {
            Arrays.fill(d[i], -1);
        }
        // int[0] 步数 int[1] 行或列号,行堆存的列号，列堆存的行号，确定位置
        PriorityQueue<int[]>[] pqrs = new PriorityQueue[n]; // pq rows
        PriorityQueue<int[]>[] pqcs = new PriorityQueue[m]; // pq cols
        for (int i = 0; i < n; i++) {
            pqrs[i] = new PriorityQueue<>((a, b) -> a[0] - b[0]); // 小根堆，按到该位置的步数
        }
        for (int i = 0; i < m; i++) {
            pqcs[i] = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        }
        d[0][0] = 1; // 起始
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {

                // 行
                // 不能到i， j的弹出直接，因为不能一步到，剩下的同行格更不可能一步到
                while (!pqrs[i].isEmpty() && grid[i][pqrs[i].peek()[1]] + pqrs[i].peek()[1] < j) {
                    pqrs[i].poll();
                }

                // 如果最后行堆中有剩余，堆顶就是我们当前单元格的一个方向的答案,比较取最小，当然在-1时直接赋值即可
                if (!pqrs[i].isEmpty()) {
                    d[i][j] = d[i][j] == -1 || d[i][pqrs[i].peek()[1]] + 1 < d[i][j] ? d[i][pqrs[i].peek()[1]] + 1 : d[i][j];
                }

                // 列
                while (!pqcs[j].isEmpty() && pqcs[j].peek()[1] + grid[pqcs[j].peek()[1]][j] < i) {
                    pqcs[j].poll();
                }
                if (!pqcs[j].isEmpty()) {
                    d[i][j] = d[i][j] == -1 || d[pqcs[j].peek()[1]][j] + 1 < d[i][j] ? d[pqcs[j].peek()[1]][j] + 1 : d[i][j];
                }

                // 如果可以到达，加入到堆中
                if (d[i][j] != -1) {
                    pqrs[i].offer(new int[]{d[i][j], j});
                    pqcs[j].offer(new int[]{d[i][j], i});
                }
            }
        }
        return d[n - 1][m - 1];
    }
}