目录
问题描述:
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
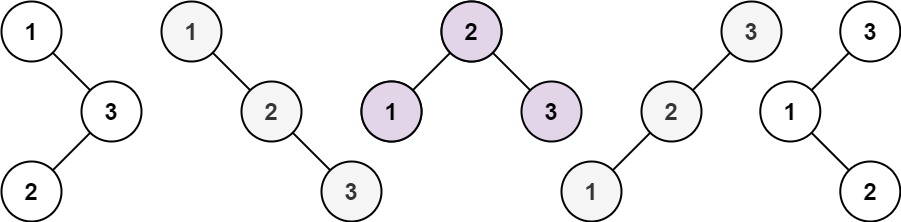
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
实现代码与解析:
动态规划:
class Solution {
public:
int numTrees(int n)
{
vector<int> dp(n+1,0);
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i < n + 1; i++)
{
for(int j = 1; j < i + 1; j++)
{
dp[i] += dp[i - j] * dp[j - 1];//各种情况加起来
}
}
return dp[n];
}
};原理思路:
代码很好写,但是用动态规划来解题其实是很难想到的,而且动态规划的递推公式也不太容易找出,如果没有提前写过,其实是很难做出来的。
主要讲讲递推公式怎么来的,首先dp数组就是表示 i 个结点的二叉搜索树的种树,头节点为 1 ~ i 的树,因为头结点已经占了一个结点,我们就把 i - 1 的结点分割在左右子树上,左右子树当然也有不同种类但结点个数相同的树,所以一种分割方式求出来的结果是相乘求出来的,最后不同分割方式相加就得到了最终结果。
其实仅仅文字这样解释依旧还是挺难想到和理解到的,画了个图,大家可以理解一下,注意不要在意结点里的值,只要符合二叉搜索树的规则就行,这里的种类仅仅是指的结构,结点值不同但结构相同的是一种。

大家可以发现画红框的是不是就是我们已经推导过的种类啊,用代码写出就是:
dp[i] += dp[i - j] * dp[j - 1];//各种情况加起来大家可以带入数字验证,顺便再次理解一下。
数学法:
class Solution {
public:
int numTrees(int n) {
long long C = 1;
for (int i = 0; i < n; ++i)
{
C = C * 2 * (2 * i + 1) / (i + 2);
}
return (int)C;
}
};
原理思路:
用的数学中的卡塔兰数,大家可以自己网上查一下。
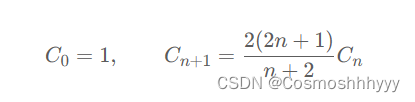





 文章探讨了如何计算给定节点数n的不同二叉搜索树的种类。主要介绍了动态规划和数学中的卡塔兰数两种方法来解决这个问题。动态规划解法通过递推公式dp[i]=Σ(dp[i-j]*dp[j-1])求解,而数学法直接利用卡塔兰数的公式进行计算。这两种方法都需要对二叉搜索树的性质有深入理解。
文章探讨了如何计算给定节点数n的不同二叉搜索树的种类。主要介绍了动态规划和数学中的卡塔兰数两种方法来解决这个问题。动态规划解法通过递推公式dp[i]=Σ(dp[i-j]*dp[j-1])求解,而数学法直接利用卡塔兰数的公式进行计算。这两种方法都需要对二叉搜索树的性质有深入理解。

















 643
643


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?









