
【导读】
这篇文章深入浅出地讲解了计算机视觉中重要的通道注意力机制——Squeeze and Excitation Networks (SENet),并提供了从理论理解到代码实现的完整指南。
当我们谈论计算机视觉中的注意力机制时,你首先想到的可能是 Vision Transformer (ViT) 架构中使用的那种。事实上,这并不是我们处理图像数据时唯一的注意力机制。还有另一种叫做挤压激励网络(Squeeze and Excitation Network, SENet)。如果说 ViT 中的注意力是空间上的操作(即给图像的不同块分配权重),那么 SENet 提出的注意力机制则是通道维度的(channel-wise),即给不同的通道分配权重。——在本文中,我们将讨论挤压激励(Squeeze and Excitation, SE)架构的工作原理、如何从零开始实现它,以及如何将该网络集成到 ResNeXt 模型中。
一、挤压激励模块
SENet 首次在题为《Squeeze-and-Excitation Networks》的论文中提出,它本身并非像 VGG、Inception 或 ResNet 那样的独立网络。相反,它是一个可以放置在现有网络中的构建块。在基于 CNN 的模型中,我们假设空间上彼此接近的像素具有高度相关性,这也是我们使用小尺寸卷积核来捕获这些相关性的原因。这种假设基本上是 CNN 的归纳偏置(inductive bias)。另一方面,SENet 引入了一种新的归纳偏置,作者假设每个图像通道对预测特定类别的贡献程度不同。通过将 SE 模块应用于 CNN,模型不仅依赖于空间模式,还能捕获每个通道的重要性。为了更好地说明这一点,我们可以想象一张火的图像,理论上红色通道对最终预测的贡献会比蓝色和绿色通道更大。
SE 模块本身的结构如图 1 所示。正如网络名称所示,该模块主要执行两个步骤:挤压(squeeze)和激励(excitation)。挤压部分对应于表示为 F_sq 的操作,而激励部分包括 F_ex 和 F_scale。另一方面,F_tr 操作实际上并不是 SE 模块的一部分。它代表了一个转换函数,原本属于应用 SE 模块的模型。例如,如果我们要将这个 SE 模块放在 ResNet 上,F_tr 操作指的是瓶颈块(bottleneck block)内的卷积层堆栈。
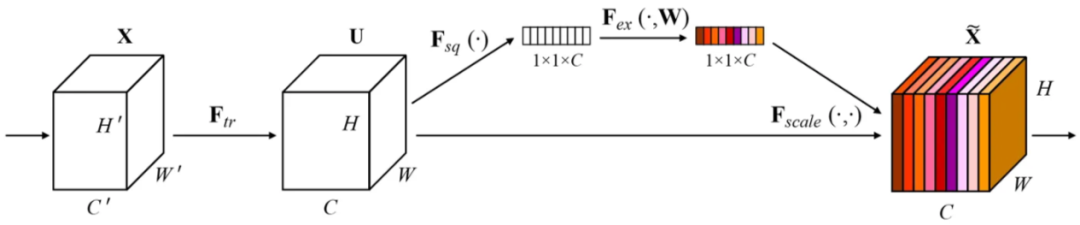
图 1. 挤压激励模块的结构
更具体地谈谈 F_sq 操作,它本质上通过利用全局平均池化(global average pooling)机制来工作,用于捕获每个通道整个空间维度的信息。通过这样做,输入张量的每个通道将由一个单一数字表示,这基本上就是对应通道的平均值。作者将此操作称为全局信息嵌入(global information embedding)。用数学语言来说,这可以正式地写成图 2 所示的公式,我们基本上将高度 H 和宽度 W 上的所有值求和,然后最终除以该通道内的像素数 (H×W)。
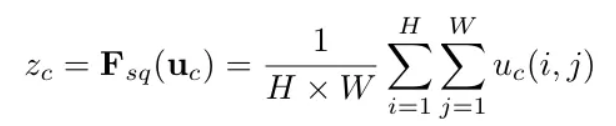
图 2. SE 模块中全局平均池化机制的数学表达式
同时,激励和缩放操作都被称为自适应重校准(adaptive recalibration),因为它们本质上所做的是根据每个通道的重要性动态调整输入张量中每个通道的权重。事实上,图 1 中的图表并未完全描绘出整个 SENet 架构。你可以在图中看到 F_ex 看起来像是一个单一操作,但它实际上由两个线性层组成,每个后面都跟着一个激活函数。详情参见下面的图 3。
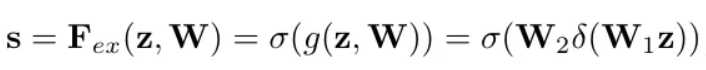
图 3. F_ex 操作的数学公式
两个线性层表示为 W_1 和 W_2,而 δ 和 σ 分别表示 ReLU 和 sigmoid 激活函数。因此,基于这个数学定义,我们稍后在实现中基本上需要做的就是将张量 z(平均池化后的张量)传递通过第一个线性层,然后是 ReLU 激活函数,第二个线性层,最后是 sigmoid 激活函数。请记住,sigmoid 函数将输入值归一化到 0 到 1 的范围内。在这种情况下,我们将把得到的输出视为每个通道的权重,其中接近 1 的值表示相应通道包含重要信息,因此我们允许模型更多地关注该通道。否则,如果结果数字接近 0,则表示相应通道对输出的贡献不大。
为了利用这些通道权重,我们可以执行 F_scale 操作,这基本上只是原始张量 u 和权重张量 s 的乘法,如下图 4 所示。通过这样做,我们本质上保留了重要通道中的值,同时抑制了不重要通道的值。

图 4. 缩放过程只是原始张量和权重张量的乘法
顺便说一下,抱歉这里有点太数学化了,哈哈。但我相信这将有助于你理解后面实现部分的代码。
二、SE 模块的放置位置
在像 VGG 这样的普通 CNN 模型上应用 SE 模块很容易,我们可以简单地将它放在每个卷积层之后。然而,在 Inception 或 ResNet 的情况下,由于这两个网络中存在并行分支,这可能就不那么直接了。为了解决这个困惑,作者提供了一个指南,专门说明如何在这两个模型上实现 SE 模块,如下图 5 所示。

图 5. SE 模块在 Inception 和 ResNet 中的放置位置
对于 Inception 模型,我们没有将 SE 模块放在每个卷积层之后,而是将输入张量通过整个 Inception 块(包括内部的所有分支),然后将 SE 模块附加在后面。相同的方法也适用于 ResNet,但请记住,跳跃连接(skip connection)中的张量与主流程之间的求和操作发生在主张量被 SE 模块处理之后。
正如我前面提到的,激励阶段本质上包含两个线性层。如果我们仔细观察上述结构,可以看到第一个线性层的输出形状是 1×1×C/r。变量 r 称为缩减比例(reduction ratio),它在通过第二个线性层最终投影回 1×1×C 之前,降低了权重张量的维度。第一个层完成的降维作为一个瓶颈操作,有助于限制模型复杂性并提高泛化能力。作者对不同 r 值进行了实验,他们发现 r = 16 在准确性和复杂性之间取得了最佳平衡。
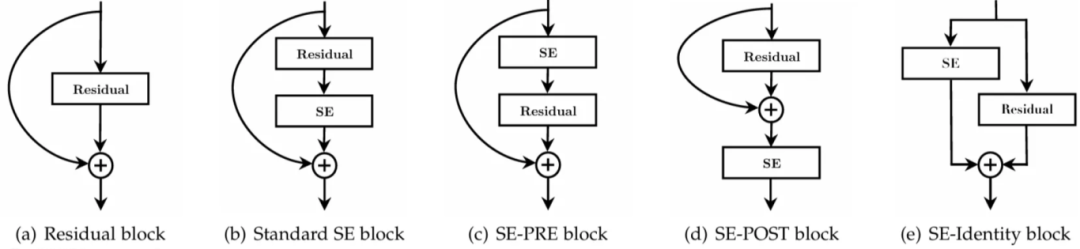
图 6. 在 ResNet 中附加 SE 模块的几种可能方式
除了在 ResNet 中实现 SE 模块之外,从图 6 可以看出,实际上有几种方法可以实现。根据图 7 中的实验结果,看起来标准 SE、SE-PRE 和 SE-Identity 块获得了相似的结果,同时它们都显著优于 SE-POST。这表明 SE 模块的放置位置会影响模型在准确性方面的性能。基于这些发现,作者认为,只要我们在逐元素求和操作之前应用 SE 模块,就会获得良好的结果。在后面的编码部分,我将演示如何实现标准的 SE 块。
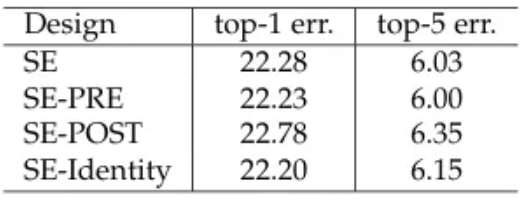
图 7. 不同 SE 模块集成策略的实验结果
三、更多实验结果
论文中实际上讨论了更多的实验结果。其中之一是一个表格,显示了将 SE 模块应用于现有基于 CNN 的模型时准确率的提高。我指的表格显示在下图 8 中。
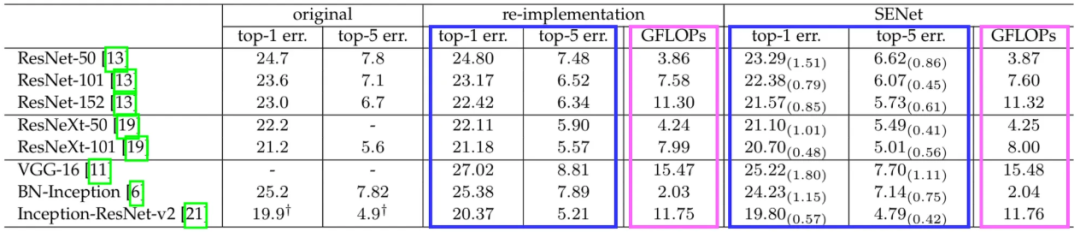
图 8. 在不同模型上应用 SE 模块的实验结果
蓝色高亮的列代表每个模型的错误率,粉色高亮的列表示以 GFLOPs 衡量的计算复杂度。重新实现(re-implementation)列指的是作者自己实现的普通模型,而 SENet 列代表配备了 SE 模块的相同模型。该表清楚地显示,当应用 SE 模块时,top-1 和 top-5 错误率都降低了。重要的是要知道,虽然添加 SE 模块会导致 GFLOPs 变高,但与错误率的降低相比,这种增加是相对微不足道的。
接下来,我们实际上可以通过在推理阶段打印 SE 模块中包含的值来揭示有趣的见解。让我们看一下下面的图 9 中的图表以便更好地说明这一点。这些图表的 x 轴表示通道号,y 轴表示根据其重要性每个通道拥有的权重,线条的颜色表示正在预测的类别。
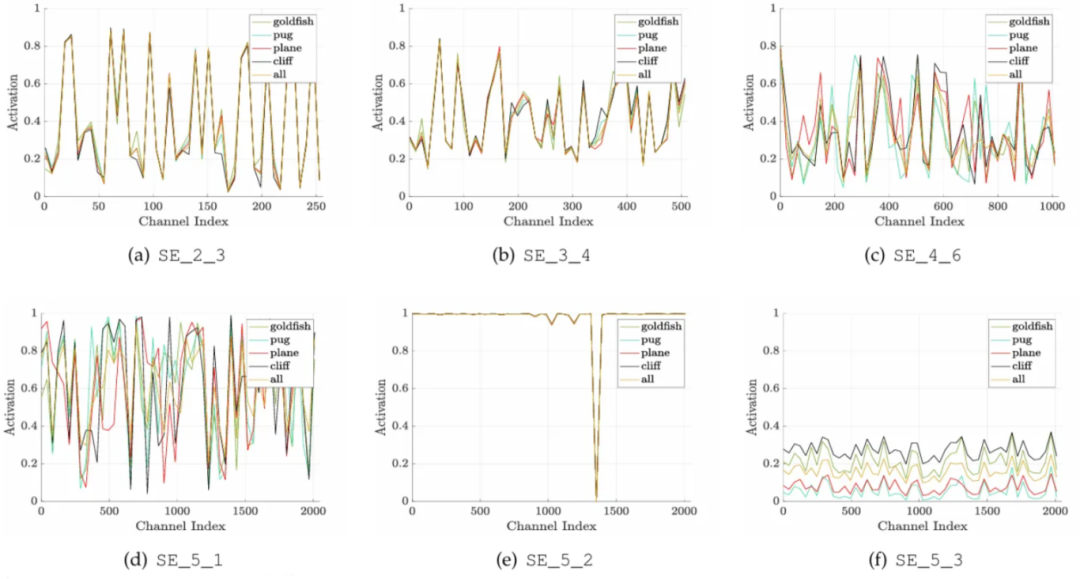
图 9. 不同网络深度下 SE 模块的激活情况
在较浅的层中,SE 模块捕获的特征是类别无关的(class-agnostic),这基本上意味着它捕获了预测所有类别所需的通用信息。称为 (a) 和 (b) 的图表,它们来自 ResNet 第 2 和第 3 阶段的 SE 模块,显示从一个类别到另一个类别的通道活动没有太大差异,表明这两个模块没有捕获关于特定类别的信息。情况在更深层的 SE 模块中实际上有所不同,即第 4 阶段 (c) 和第 5 阶段 (d) 的模块。我们可以看到这两个模块根据预测的类别不同而不同地调整通道权重。这本质上是更深层的 SE 模块被称为类别特定(class-specific)的原因。然而,作者承认,在某些 SE 模块中可能会发生异常行为,这发生在第 5 阶段的第 2 个块中 (e)。这里的 SE 模块没有显示出有意义的通道重校准行为,表明它的贡献不如我们之前讨论的那些模块大。
四、详细架构
在本文中,我们将实现 SE-ResNeXt-50 (32×4d) 模型,在图 10 中它对应于最右边的一列。ResNeXt 模型本身与 ResNet 类似,只是每个块内第二个卷积层的组参数被设置为 32。如果你熟悉 ResNeXt,这本质上是实现所谓基数(cardinality)的最简单但有效的方法。
仔细看这个架构,SE-ResNet-50 与 ResNet-50 的区别仅在于 SE 模块的存在。同样的情况也适用于 SE-ResNeXt-50 (32×4d) 与 ResNeXt-50 (32×4d) 的比较(未在表格中显示)。注意在下图中,带有 SE 模块的模型在每个块内的最后一个卷积层之后附加了一个 fc 层,其中对应的两个数字表示 SE 模块内部的第一和第二个全连接层。
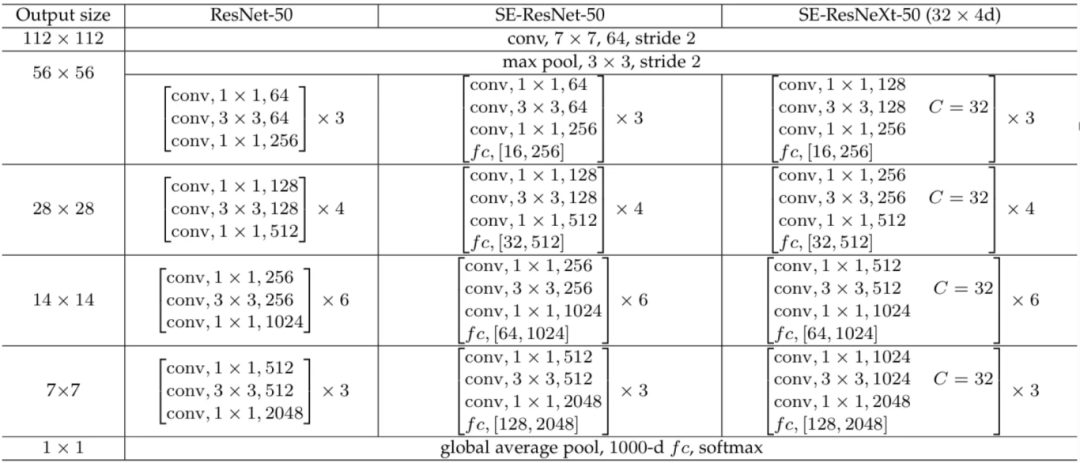
图 10. ResNet-50、SE-ResNet-50 和 SE-ResNeXt-50 (32×4d) 的完整架构
五、从零开始实现
请记住,我们这里要将 SE 模块集成到 ResNeXt 上,所以我们需要从头开始实现它们两者。从技术上讲,实际上可以直接从 PyTorch 获取 ResNeXt 架构,然后手动将 SE 模块附加上去。然而,这里我决定使用我上一篇文章中的 ResNeXt 实现,因为我觉得它比 PyTorch 的实现更容易理解。请注意,这里我将重点放在构建 SE 模块以及如何将其附加到 ResNeXt 模型上,而不是解释 ResNeXt 本身。
现在让我们通过导入所需的模块来开始编码。
# 代码块 1
import torch
import torch.nn as nn
-
挤压激励模块
下面的 SE 模块实现遵循图 5(右)所示的图表。值得注意的是,下面的 SEModule 类不包括跳跃连接(弯曲的箭头),因为整个 SE 模块是在初始分支之后但在合并(求和)之前应用的。
这个类的 __init__() 方法接受两个参数:num_channels 和 r,如代码块 2a 中的行 #(1) 所示。我们肯定希望这个 SE 模块可以在整个网络中使用。因此,我们需要将 num_channels 参数设置为可调整的,因为输出通道的数量在不同阶段的 ResNeXt 块之间是不同的,如图 10 所示。同时,尽管我们通常在整个网络的 SE 模块中使用相同的缩减比例 r,但从技术上讲,我们可以为不同的阶段使用不同的 r,这可能是一个有趣的事情来实验。所以,这基本上就是我为什么也将 r 参数设置为可调整的原因。
# 代码块 2a
class SEModule(nn.Module):
def __init__(self, num_channels, r): #(1)
super().__init__()
self.global_pooling = nn.AdaptiveAvgPool2d(output_size=(1,1)) #(2)
self.fc0 = nn.Linear(in_features=num_channels, #(3)
out_features=num_channels//r,
bias=False)
self.relu = nn.ReLU() #(4)
self.fc1 = nn.Linear(in_features=num_channels//r, #(5)
out_features=num_channels,
bias=False)
self.sigmoid = nn.Sigmoid() #(6)
我们需要在 __init__() 方法内部初始化 5 个层。我按照图 5 中给出的顺序编写它们,即全局平均池化层 (#(2))、线性层 (#(3))、ReLU 激活函数 (#(4))、另一个线性层 (#(5)) 和 sigmoid 激活函数 (#(6))。在这里你可以看到,第一个线性层通过将通道数从 num_channels 缩减到 num_channels//r 来执行降维,然后第二个线性层将其扩展回 num_channels。请注意,我们将两个线性层的偏置项(bias)设置为 False,这实质上意味着我们将只使用权重张量。两个层中偏置项的缺失迫使 SE 模块学习一个通道与其他通道的相关性,而不是仅仅添加固定的调整。
仍然是 SEModule 类,现在让我们转到 forward() 方法来定义网络流。你可以在代码块 2b 中的行 #(1) 看到,我们从单个输入 x 开始,在 ResNeXt 的情况下,它本质上是由同一 ResNeXt 块内的第三个卷积层产生的张量。如图 5 所示,我们接下来需要做的是将网络分支出来。这里我们直接使用 global_pooling 层处理分支,我将结果张量命名为 squeezed (#(2))。原始输入张量 x 本身将保持不变,因为在缩放阶段之前我们不会对它执行任何操作。接下来,我们需要使用 torch.flatten() 去掉 squeezed 张量的空间维度 (#(3))。这基本上是因为我们想用行 #(4) 和 #(5) 的线性层进一步处理它,这些层只能处理单维张量。空间维度然后在行 #(6) 被重新引入,允许我们在行 #(7) 执行 x(原始张量)和 excited(通道权重)之间的乘法。这整个过程产生了 x 的重校准版本,我们称之为 scaled。这里我在每一步之后打印出张量维度,以便你更好地理解这个 SE 模块的流程。
# 代码块 2b
def forward(self, x): #(1)
print(f'original\t\t: {x.size()}')
squeezed = self.global_pooling(x) #(2)
print(f'after avgpool\t\t: {squeezed.size()}')
squeezed = torch.flatten(squeezed, 1) #(3)
print(f'after flatten\t\t: {squeezed.size()}')
excited = self.relu(self.fc0(squeezed)) #(4)
print(f'after fc0-relu\t\t: {excited.size()}')
excited = self.sigmoid(self.fc1(excited)) #(5)
print(f'after fc1-sigmoid\t: {excited.size()}')
excited = excited[:, :, None, None] #(6)
print(f'after reshape\t\t: {excited.size()}')
scaled = x * excited #(7)
print(f'after scaling\t\t: {scaled.size()}')
return scaled
现在我们将通过传递一个虚拟张量(dummy tensor)来测试我们是否正确实现了网络。在下面的代码块 3 中,我初始化了一个 SE 模块,并将其配置为接受 512 个通道的图像张量,并具有 16 的缩减比例 (#(1))。如果你查看图 10 中的 SE-ResNeXt 架构,这个 SE 模块基本上对应于第三阶段中的那个(输出大小为 28×28)。因此,在行 #(2) 我们需要相应地调整虚拟张量的形状。然后我们使用行 #(3) 的代码将这个张量输入网络。
# 代码块 3
semodule = SEModule(num_channels=512, r=16) #(1)
x = torch.randn(1, 512, 28, 28) #(2)
out = semodule(x) #(3)
# 代码块 3 输出
original : torch.Size([1, 512, 28, 28]) #(1)
after avgpool : torch.Size([1, 512, 1, 1]) #(2)
after flatten : torch.Size([1, 512]) #(3)
after fc0-relu : torch.Size([1, 32]) #(4)
after fc1-sigmoid : torch.Size([1, 512]) #(5)
after reshape : torch.Size([1, 512, 1, 1]) #(6)
after scaling : torch.Size([1, 512, 28, 28]) #(7)
你可以看到原始张量形状与我们的虚拟张量完全匹配,即 1×512×28×28 (#(1))。顺便说一下,我们可以忽略第 0 轴上的数字 1,因为它本质上表示批次大小(batch size),在这种情况下我假设一个批次中只有一张图像。在被池化后,空间维度坍缩为 1×1,因为现在每个通道由一个单一数字表示 (#(2))。我之前解释的展平操作(flatten)的目的是去掉两个空轴 (#(3)),因为后续的线性层只能处理单维张量。在这里你可以看到,第一个线性层将张量维度减少到 32,这要归功于我们之前设置为 16 的缩减比例 (#(4))。这个张量的长度然后被第二个线性层扩展回 512 (#(5))。接下来,我们 unsqueeze 张量,以便取回我们的 1×1 空间维度 (#(6)),允许我们将其与输入张量相乘 (#(7))。基于这个详细的流程,你可以看到一个 SE 模块基本上保留了原始张量维度,证明这个模块可以附加到任何基于 CNN 的模型上,而不会破坏网络的原始流程。
-
ResNeXt
既然我们已经理解了如何从零开始实现 SE 模块,现在我将向你展示如何将它附加到 ResNeXt 模型上。在这样做之前,我们需要初始化实现 ResNeXt 架构所需的参数。在下面的代码块 4 中,前四个变量是根据 ResNeXt-50 (32×4d) 变体确定的,而最后一个 (R) 代表 SE 模块的缩减比例。
# 代码块 4
CARDINALITY = 32
NUM_CHANNELS = [3, 64, 256, 512, 1024, 2048]
NUM_BLOCKS = [3, 4, 6, 3]
NUM_CLASSES = 1000
R = 16
代码块 5a 和 5b 中定义的 Block 类来自我之前的文章。在 __init__() 方法中我们实际上做了很多事情,但总体思路是,我们初始化三个卷积层,称为 conv0 (#(1))、conv1 (#(2)) 和 conv2 (#(3)),然后在行 #(4) 初始化 SE 模块。我们将根据图 10 所示的 SE-ResNeXt 架构来配置这些层。
# 代码块 5a
class Block(nn.Module):
def __init__(self,
in_channels,
add_channel=False,
channel_multiplier=2,
downsample=False):
super().__init__()
self.add_channel = add_channel
self.channel_multiplier = channel_multiplier
self.downsample = downsample
if self.add_channel:
out_channels = in_channels*self.channel_multiplier
else:
out_channels = in_channels
mid_channels = out_channels//2
if self.downsample:
stride = 2
else:
stride = 1
if self.add_channel or self.downsample:
self.projection = nn.Conv2d(in_channels=in_channels,
out_channels=out_channels,
kernel_size=1,
stride=stride,
padding=0,
bias=False)
nn.init.kaiming_normal_(self.projection.weight, nonlinearity='relu')
self.bn_proj = nn.BatchNorm2d(num_features=out_channels)
self.conv0 = nn.Conv2d(in_channels=in_channels, #(1)
out_channels=mid_channels,
kernel_size=1,
stride=1,
padding=0,
bias=False)
nn.init.kaiming_normal_(self.conv0.weight, nonlinearity='relu')
self.bn0 = nn.BatchNorm2d(num_features=mid_channels)
self.conv1 = nn.Conv2d(in_channels=mid_channels, #(2)
out_channels=mid_channels,
kernel_size=3,
stride=stride,
padding=1,
bias=False,
groups=CARDINALITY)
nn.init.kaiming_normal_(self.conv1.weight, nonlinearity='relu')
self.bn1 = nn.BatchNorm2d(num_features=mid_channels)
self.conv2 = nn.Conv2d(in_channels=mid_channels, #(3)
out_channels=out_channels,
kernel_size=1,
stride=1,
padding=0,
bias=False)
nn.init.kaiming_normal_(self.conv2.weight, nonlinearity='relu')
self.bn2 = nn.BatchNorm2d(num_features=out_channels)
self.relu = nn.ReLU()
self.semodule = SEModule(num_channels=out_channels, r=R) #(4)
forward() 方法本身通常也与原始 ResNeXt 模型相同,只是这里我们需要在逐元素求和之前放置 SE 模块,如下面代码块 5b 中的行 #(1) 所示。请记住,这个实现遵循图 6 (b) 中的标准 SE 块架构。
# 代码块 5b
def forward(self, x):
print(f'original\t\t: {x.size()}')
if self.add_channel or self.downsample:
residual = self.bn_proj(self.projection(x))
print(f'after projection\t: {residual.size()}')
else:
residual = x
print(f'no projection\t\t: {residual.size()}')
x = self.conv0(x)
x = self.bn0(x)
x = self.relu(x)
print(f'after conv0-bn0-relu\t: {x.size()}')
x = self.conv1(x)
x = self.bn1(x)
x = self.relu(x)
print(f'after conv1-bn1-relu\t: {x.size()}')
x = self.conv2(x)
x = self.bn2(x)
print(f'after conv2-bn2\t\t: {x.size()}')
x = self.semodule(x) #(1)
print(f'after semodule\t\t: {x.size()}')
x = x + residual
x = self.relu(x)
print(f'after summation\t\t: {x.size()}')
return x
通过上述实现,每次我们实例化一个 Block 对象时,我们将得到一个已经配备了 SE 模块的 ResNeXt 块。现在我们将测试上面的类,看看我们是否正确地实现了它。这里我将模拟第三阶段内的一个 ResNeXt 块。add_channel 和 downsample 参数设置为 False,因为我们希望保留输入张量的通道数和空间维度。
# 代码块 6
block = Block(in_channels=512, add_channel=False, downsample=False)
x = torch.randn(1, 512, 28, 28)
out = block(x)
下面是输出的样子。在这里你可以看到,我们的第一个卷积层成功地将通道数从 512 减少到 256 (#(1)),然后由第三个卷积层扩展回其原始维度 (#(2))。之后,张量通过 SE 块,其输出大小与其输入相同,就像我们之前在代码块 3 中看到的那样 (#(3))。随着 SE 模块处理的完成,我们最终可以执行主分支的张量与跳跃连接中的张量之间的逐元素求和 (#(4))。
original : torch.Size([1, 512, 28, 28])
no projection : torch.Size([1, 512, 28, 28])
after conv0-bn0-relu : torch.Size([1, 256, 28, 28]) #(1)
after conv1-bn1-relu : torch.Size([1, 256, 28, 28])
after conv2-bn2 : torch.Size([1, 512, 28, 28]) #(2)
after semodule : torch.Size([1, 512, 28, 28]) #(3)
after summation : torch.Size([1, 512, 28, 28]) #(4)
下面是我实现整个架构的方式。我们本质上需要做的就是根据图 10 中的架构堆叠多个 SE-ResNeXt 块。事实上,因为 SE-ResNeXt 与原始 ResNeXt 的不同之处仅在于我们之前讨论的 Block 类中存在 SE 模块。
# 代码块 7
class SEResNeXt(nn.Module):
def __init__(self):
super().__init__()
# conv1 stage
self.resnext_conv1 = nn.Conv2d(in_channels=NUM_CHANNELS[0],
out_channels=NUM_CHANNELS[1],
kernel_size=7,
stride=2,
padding=3,
bias=False)
nn.init.kaiming_normal_(self.resnext_conv1.weight,
nonlinearity='relu')
self.resnext_bn1 = nn.BatchNorm2d(num_features=NUM_CHANNELS[1])
self.relu = nn.ReLU()
self.resnext_maxpool1 = nn.MaxPool2d(kernel_size=3,
stride=2,
padding=1)
# conv2 stage
self.resnext_conv2 = nn.ModuleList([
Block(in_channels=NUM_CHANNELS[1],
add_channel=True,
channel_multiplier=4,
downsample=False)
])
for _ in range(NUM_BLOCKS[0]-1):
self.resnext_conv2.append(Block(in_channels=NUM_CHANNELS[2]))
# conv3 stage
self.resnext_conv3 = nn.ModuleList([Block(in_channels=NUM_CHANNELS[2],
add_channel=True,
downsample=True)])
for _ in range(NUM_BLOCKS[1]-1):
self.resnext_conv3.append(Block(in_channels=NUM_CHANNELS[3]))
# conv4 stage
self.resnext_conv4 = nn.ModuleList([Block(in_channels=NUM_CHANNELS[3],
add_channel=True,
downsample=True)])
for _ in range(NUM_BLOCKS[2]-1):
self.resnext_conv4.append(Block(in_channels=NUM_CHANNELS[4]))
# conv5 stage
self.resnext_conv5 = nn.ModuleList([Block(in_channels=NUM_CHANNELS[4],
add_channel=True,
downsample=True)])
for _ in range(NUM_BLOCKS[3]-1):
self.resnext_conv5.append(Block(in_channels=NUM_CHANNELS[5]))
self.avgpool = nn.AdaptiveAvgPool2d(output_size=(1,1))
self.fc = nn.Linear(in_features=NUM_CHANNELS[5],
out_features=NUM_CLASSES)
def forward(self, x):
print(f'original\t\t: {x.size()}')
x = self.relu(self.resnext_bn1(self.resnext_conv1(x)))
print(f'after resnext_conv1\t: {x.size()}')
x = self.resnext_maxpool1(x)
print(f'after resnext_maxpool1\t: {x.size()}')
for i, block in enumerate(self.resnext_conv2):
x = block(x)
print(f'after resnext_conv2 #{i}\t: {x.size()}')
for i, block in enumerate(self.resnext_conv3):
x = block(x)
print(f'after resnext_conv3 #{i}\t: {x.size()}')
for i, block in enumerate(self.resnext_conv4):
x = block(x)
print(f'after resnext_conv4 #{i}\t: {x.size()}')
for i, block in enumerate(self.resnext_conv5):
x = block(x)
print(f'after resnext_conv5 #{i}\t: {x.size()}')
x = self.avgpool(x)
print(f'after avgpool\t\t: {x.size()}')
x = torch.flatten(x, start_dim=1)
print(f'after flatten\t\t: {x.size()}')
x = self.fc(x)
print(f'after fc\t\t: {x.size()}')
return x
随着整个 SE-ResNeXt-50 (32×4d) 架构的完成,我们现在将通过传递一个大小为 1×3×224×224 的张量来测试它,模拟一个大小为 224×224 的单个 RGB 图像。你可以在下面代码块 8 的输出中看到,模型似乎工作正常,因为张量成功通过了 seresnext 模型内的所有层而没有返回任何错误。因此,我相信这个模型现在可以训练了。顺便说一下,如果你想实际训练这个模型,不要忘记根据数据集中类的数量更改输出通道中的神经元数量。
# 代码块 8
seresnext = SEResNeXt()
x = torch.randn(1, 3, 224, 224)
out = seresnext(x)
# 代码块 8 输出
original : torch.Size([1, 3, 224, 224])
after resnext_conv1 : torch.Size([1, 64, 112, 112])
after resnext_maxpool1 : torch.Size([1, 64, 56, 56])
after resnext_conv2 #0 : torch.Size([1, 256, 56, 56])
after resnext_conv2 #1 : torch.Size([1, 256, 56, 56])
after resnext_conv2 #2 : torch.Size([1, 256, 56, 56])
after resnext_conv3 #0 : torch.Size([1, 512, 28, 28])
after resnext_conv3 #1 : torch.Size([1, 512, 28, 28])
after resnext_conv3 #2 : torch.Size([1, 512, 28, 28])
after resnext_conv3 #3 : torch.Size([1, 512, 28, 28])
after resnext_conv4 #0 : torch.Size([1, 1024, 14, 14])
after resnext_conv4 #1 : torch.Size([1, 1024, 14, 14])
after resnext_conv4 #2 : torch.Size([1, 1024, 14, 14])
after resnext_conv4 #3 : torch.Size([1, 1024, 14, 14])
after resnext_conv4 #4 : torch.Size([1, 1024, 14, 14])
after resnext_conv4 #5 : torch.Size([1, 1024, 14, 14])
after resnext_conv5 #0 : torch.Size([1, 2048, 7, 7])
after resnext_conv5 #1 : torch.Size([1, 2048, 7, 7])
after resnext_conv5 #2 : torch.Size([1, 2048, 7, 7])
after avgpool : torch.Size([1, 2048, 1, 1])
after flatten : torch.Size([1, 2048])
after fc : torch.Size([1, 1000])
此外,我们还可以使用以下代码打印出该模型拥有的参数数量。在这里你可以看到,代码块返回 27,543,848。这个参数数量略高于原始 ResNeXt 模型的对应物,后者只有 25,028,904 个参数。模型大小的这种增加肯定是合理的,因为由于 SE 模块的存在,整个网络中的 ResNeXt 块现在有了更多的层。
# 代码块 9
def count_parameters(model):
return sum([params.numel() for params in model.parameters()])
count_parameters(seresnext)
最后总结
关于挤压激励模块的内容就这些了。我确实鼓励你从这里开始探索,在你自己的数据集上训练这个模型,这样你就会看到论文中提出的发现是否也适用于你的情况。不仅如此,如果你尝试自己将 SE 模块实现到其他神经网络架构(如 VGG 或 Inception)上,我认为也会很有趣。
希望你今天学到了一些新东西。感谢阅读!






















 55
55

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








