单片空间后方交会（最详细原理、代码、结果分析）

是白的小宇

已于 2024-06-05 11:07:02 修改

阅读量6.1k

点赞数 42

CC 4.0 BY-SA版权

分类专栏：摄影测量学文章标签：算法 c++ 图像处理数码相机空间计算

于 2024-06-05 11:03:37 首次发布

本文链接：https://blog.youkuaiyun.com/Compass_love/article/details/139420150

摄影测量学专栏收录该内容

4 篇文章

订阅专栏

使用数据：控制点物方空间坐标、控制点像平面量测坐标

误差方程式：共线条件方程

误差方程观测值：像点量测坐标

误差方程未知数（改正值），本文我使用最全面的改正方程：外方位元素、内方位元素、畸变系数（可根据需求减少未知数，删除未知数改正值和对应的系数即可）

程序流程：打开控制点物方坐标文件、控制点像点坐标文件读取数据，并根据合适的控制点，按照共线条件方程的空间后方交会误差方程形式，将像点坐标观测值作为观测值，将外方位元素改正值、内方位元素改正值、畸变系数改正值作为未知数，并设定合适的起算数据进行迭代解算。计算相片的内外方位元素和畸变系数（k1，k2，p1，p2）。并计算统计精度，保证中误差和残差在一定限度内。

统计计算精度：单位权中误差、未知数中误差、像点观测值残差。

一、单片空间后方交会原理

使用控制点物方坐标文件、控制点像点量测坐标文件，读入数据并保存在二维点、三维点数据结构中。然后将对应点的像平面坐标和物方坐标连接，保存成一条数据，便于后续使用。根据共线条件方程误差方程的空间后方交会形式，将像点量测值作为观测值，将内外方位元素、畸变系数（k1，k2，p1，p2）的改正值作为未知数，设定一个未知数的起算估计值进行迭代，求解最终的相片内外方位元素和畸变系数（k1，k2，p1，p2）。

1.1误差方程构建

定义旋转矩阵为：

基于共线条件方程：

线性化后得到误差方程的一般形式，其中未知数为：

误差方程一般式为：

（其中At为外方位元素、BcXc为控制点、BuXu为待定点、DadXad为畸变系数的系数及改正值，L为观测值误差项）

而后方交会的误差方程式将内外方位元素和畸变系数作为未知数：

1.2误差方程系数填充

其中：

畸变模型选用：

各系数的定义如下：

Dad即使用畸变模型对应未知数改正值前的系数即可。

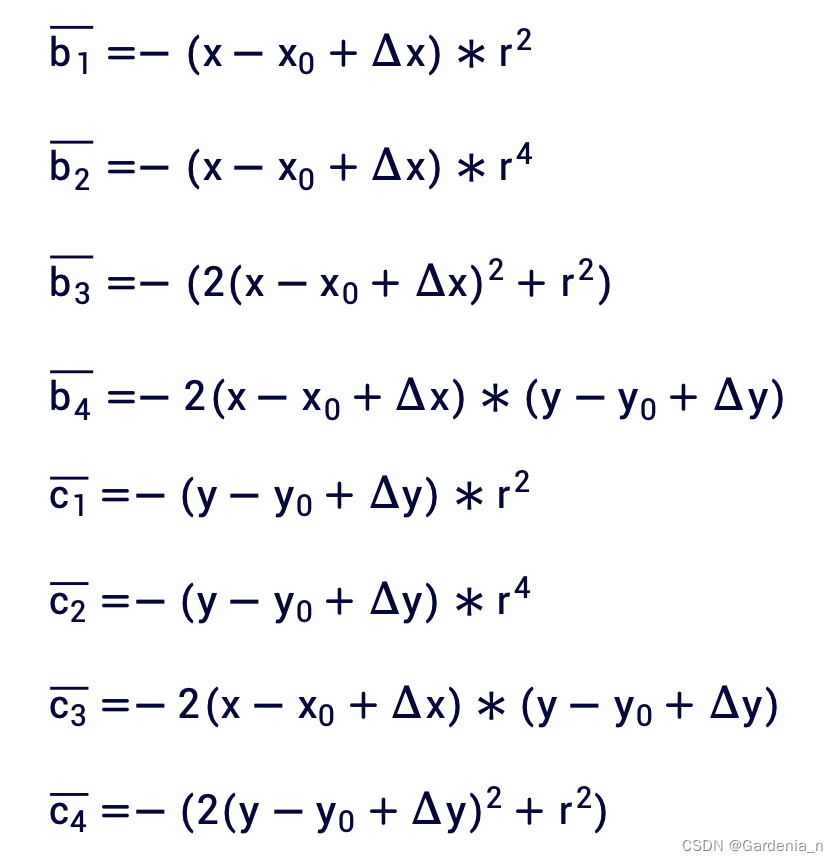
系数求解中使用到的 $\bar{Z}$ 为像空间坐标系下的物方点坐标，故首先需要将控制点的物方坐标从物方坐标系转换到像空间坐标系S-xyz下：

观测值误差项， $\Delta x$ 与 $\Delta y$ 使用畸变模型求解：

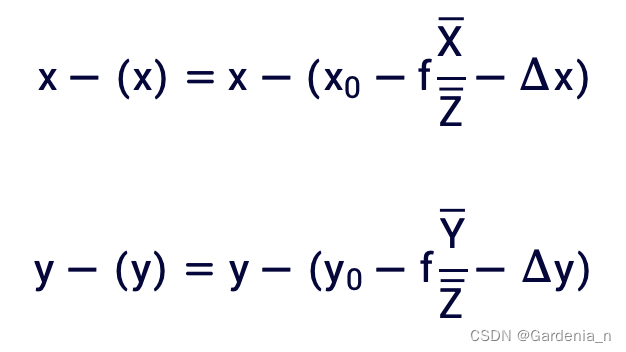
1.3初始值（起算值）设置

1.4逐点计算，合并系数矩阵

将所有的像点都计算得到一个误差方程，计算每一个像点对应的误差方程未知数系数和误差项，并将所有的系数阵放在一起求解，系数合并为大系数阵A，大小为（2*num_of_points）*13（13为未知数/改正数的个数，结合实际求解未知数设置），观测值误差阵合并为L，L矩阵大小为（2*num_of_points）*1。

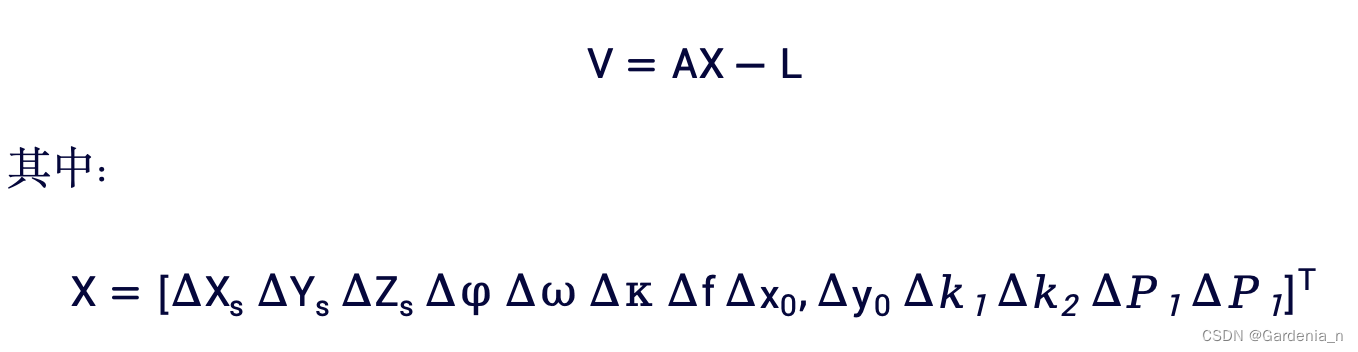
1.5迭代计算求最优解

最后利用最小二乘平差原理，计算未知数改正值：

将所有的未知数加上计算得到的改正数，得到新的值，再次代回第一步迭代计算，直到每一项的改正值小于某一个阈值为止（我设置的是0.0001）。输出最后得到的未知数平差计算结果。

1.6精度统计

二、单片空间后方交会代码

#include <opencv2/highgui.hpp>  
#include <opencv2/core.hpp>  
//#include <iostream>
#include <math.h>
#include<fstream>
#include<sstream>
#include<vector>
#include<iostream>
#include<iomanip>

using namespace std;
using namespace cv;
//  控制场平面坐标系
//  ^ X
//  |
//  |
//  |——————> Y(左手系和右手系的转换）



#define Pi 3.14159265
#define ROWS 4160
#define COLS 6240
#define PIXSIZE 0.00376 
//--------------------------结构体申明--------------------------------------

struct ControlPoint
{
	int flag;
	double X;
	double Y;
	double Z;
};

struct imgPoint
{
	int flag;
	double x;
	double y;
};

struct merge_point
{
	int flag;
	double X;
	double Y;
	double Z;
	double x;
	double y;
};

//方位元素和畸变系数
struct orienParam {
	//内方位元素
	double x0 = 0;
	double y0 = 0;
	double f = 0;
	//畸变系数
	double k1 = 0;
	double k2 = 0;
	double p1 = 0;
	double p2 = 0;
	//外方位元素
	double Phi = 0;
	double Omega = 0;
	double Kappa = 0;
	double Xs = 0;
	double Ys = 0;
	double Zs = 0;
};

//------------------坐标文件读取与坐标系变换---------------------

//  标志点量测坐标定义       标志点像平面坐标定义
//  --------> x(pixel)            ^ y(mm)  -(y-COLS/2)
//  |                             |    
//  |                             |            
//  |                     -----------------> x (x-ROWS/2)
//  |                             |
//   y                            |    
// 

void Pixel2Img_with_co_change(vector<imgPoint>& imgPoints)
{
	for (int i = 0; i < imgPoints.size(); i++)
	{
		imgPoints[i].x = (imgPoints[i].x - COLS / 2) * PIXSIZE;
		imgPoints[i].y = -1.0 * (imgPoints[i].y - ROWS / 2) * PIXSIZE;
	}
}


void readctrl_ptData(char* file, vector<ControlPoint>& ControlPoints)
{
	ifstream inFile(file);
	if (!inFile)
	{
		cout << "文件读取失败，请检查文件路径" << endl;
		return;
	}
	string line;
	string firstLine;
	getline(inFile, firstLine);
	while (getline(inFile, line)) {
		ControlPoint ctrl_pt;
		istringstream iss(line);
		iss >> ctrl_pt.flag;
		//坐标系转换
		iss >> ctrl_pt.Z;
		iss >> ctrl_pt.X;
		iss >> ctrl_pt.Y;
		ctrl_pt.Z = -1.0 * ctrl_pt.Z;
 /* Z                  Y
	|  X               | 
	| /         =>     |______>X
	|/                /
	————————>Y       /Z              */
		ControlPoints.push_back(ctrl_pt);
	}
	inFile.close();
}

void readImgData(char* file, vector<imgPoint>& imgPoints)
{
	ifstream inFile(file);
	if (!inFile)
	{
		cout << "文件读取失败，请检查文件路径" << endl;
		return;
	}
	string line;
	while (getline(inFile, line)) {
		imgPoint img_pt;
		istringstream iss(line);
		iss >> img_pt.flag;
		iss >> img_pt.x;
		iss >> img_pt.y;
		imgPoints.push_back(img_pt);
	}
	inFile.close();
}

void Merge_Point(vector<imgPoint>& imgPoints, vector<ControlPoint>& ControlPoints, vector<merge_point>& merge_points)
{
	merge_point pair;
	for (int i = 0; i < imgPoints.size(); i++)
	{
		for (int j = 0; j < ControlPoints.size(); j++)
		{
			if (imgPoints[i].flag == ControlPoints[j].flag)
			{
				pair.flag = imgPoints[i].flag;
				pair.X = ControlPoints[j].X;
				pair.Y = ControlPoints[j].Y;
				pair.Z = ControlPoints[j].Z;
				pair.x = imgPoints[i].x;
				pair.y = imgPoints[i].y;
				merge_points.push_back(pair);
				break;
			}
		}
	}
}

//-----------------误差方程建立------------------------

void cal_Coefficient(Mat& A, Mat& l, vector<merge_point>& merge_points, orienParam& orien)
{
	double x0 = orien.x0;
	double y0 = orien.y0;
	double f = orien.f;
	double k1 = orien.k1;
	double k2 = orien.k2;
	double p1 = orien.p1;
	double p2 = orien.p2;
	double Phi = orien.Phi;
	double Omega = orien.Omega;
	double Kappa = orien.Kappa;
	double Xs = orien.Xs;
	double Ys = orien.Ys;
	double Zs = orien.Zs;
	//计算旋转矩阵
	Mat R = Mat::zeros(3, 3, CV_64FC1);
	R.at<double>(0, 0) = cos(Phi) * cos(Kappa) - sin(Phi) * sin(Omega) * sin(Kappa);
	R.at<double>(0, 1) = -1.0 * cos(Phi) * sin(Kappa) - sin(Phi) * sin(Omega) * cos(Kappa);
	R.at<double>(0, 2) = -1.0 * sin(Phi) * cos(Omega);
	R.at<double>(1, 0) = cos(Omega) * sin(Kappa);
	R.at<double>(1, 1) = cos(Omega) * cos(Kappa);
	R.at<double>(1, 2) = -1.0 * sin(Omega);
	R.at<double>(2, 0) = sin(Phi) * cos(Kappa) + cos(Phi) * sin(Omega) * sin(Kappa);
	R.at<double>(2, 1) = -1.0 * sin(Phi) * sin(Kappa) + cos(Phi) * sin(Omega) * cos(Kappa);
	R.at<double>(2, 2) = cos(Phi) * cos(Omega);
	for (int i = 0; i < merge_points.size(); i++)
	{
		double X = merge_points[i].X;
		double Y = merge_points[i].Y;
		double Z = merge_points[i].Z;
		double x = merge_points[i].x;
		double y = merge_points[i].y;
		double r_2 = pow(x - x0, 2) + pow(y - y0, 2);
		double delta_x = (x - x0) * (k1 * r_2 + k2 * r_2 * r_2) + p1 * (r_2 + pow((x - x0), 2)) + 2 * p2 * (x - x0) * (y - y0);
		double delta_y = (y - y0) * (k1 * r_2 + k2 * r_2 * r_2) + p2 * (r_2 + pow((y - y0), 2)) + 2 * p1 * (x - x0) * (y - y0);
		double Xbar = R.at<double>(0, 0) * (X - Xs) + R.at<double>(1, 0) * (Y - Ys) + R.at<double>(2, 0) * (Z - Zs);
		double Ybar = R.at<double>(0, 1) * (X - Xs) + R.at<double>(1, 1) * (Y - Ys) + R.at<double>(2, 1) * (Z - Zs);
		double Zbar = R.at<double>(0, 2) * (X - Xs) + R.at<double>(1, 2) * (Y - Ys) + R.at<double>(2, 2) * (Z - Zs);
		//外方位元素系数->线元素
		double a11 = (R.at<double>(0, 0) * f + R.at<double>(0, 2) * (x - x0 + delta_x)) / Zbar;
		double a12 = (R.at<double>(1, 0) * f + R.at<double>(1, 2) * (x - x0 + delta_x)) / Zbar;
		double a13 = (R.at<double>(2, 0) * f + R.at<double>(2, 2) * (x - x0 + delta_x)) / Zbar;
		double a21 = (R.at<double>(0, 1) * f + R.at<double>(0, 2) * (y - y0 + delta_y)) / Zbar;
		double a22 = (R.at<double>(1, 1) * f + R.at<double>(1, 2) * (y - y0 + delta_y)) / Zbar;
		double a23 = (R.at<double>(2, 1) * f + R.at<double>(2, 2) * (y - y0 + delta_y)) / Zbar;
		//外方位元素系数->角元素
		double a14 = (y - y0 + delta_y) * sin(Omega) - (((x - x0 + delta_x) / f) * ((x - x0 + delta_x) * cos(Kappa) - (y - y0 + delta_y) * sin(Kappa)) + f * cos(Kappa)) * cos(Omega);
		double a15 = -f * sin(Kappa) - ((x - x0 + delta_x) / f) * ((x - x0 + delta_x) * sin(Kappa) + (y - y0 + delta_y) * cos(Kappa));
		double a16 = y - y0 + delta_y;
		double a24 = -1.0 * (x - x0 + delta_x) * sin(Omega) - (((y - y0 + delta_y) / f) * ((x - x0 + delta_x) * cos(Kappa) - (y - y0 + delta_y) * sin(Kappa)) - f * sin(Kappa)) * cos(Omega);
		double a25 = -f * cos(Kappa) - ((y - y0 + delta_y) / f) * ((x - x0 + delta_x) * sin(Kappa) + (y - y0 + delta_y) * cos(Kappa));
		double a26 = -1.0 * (x - x0 + delta_x);
		//内方位元素系数
		double a17 = (x - x0 + delta_x) / f;
		double a18 = 1;
		double a19 = 0;
		double a27 = (y - y0 + delta_y) / f;
		double a28 = 0;
		double a29 = 1;
		//畸变系数
		double a110 = -1.0 * (x - x0 + delta_x) * r_2;                      //k1
		double a111 = -1.0 * (x - x0 + delta_x) * r_2 * r_2;				//k2
		double a112 = -1.0 * (2 * pow((x - x0 + delta_x), 2) + r_2);	    //p1
		double a113 = -2.0 * (y - y0 + delta_y) * (x - x0 + delta_x);		//p2
		double a210 = -1.0 * (y - y0 + delta_y) * r_2;                      //k1
		double a211 = -1.0 * (y - y0 + delta_y) * r_2 * r_2;                //k2        
		double a212 = -2.0 * (y - y0 + delta_y) * (x - x0 + delta_x);	    //p1
		double a213 = -1.0 * (2 * pow((y - y0 + delta_y), 2) + r_2);        //p2

		//组合为系数阵
		A.at<double>(2 * i, 0) = a11; A.at<double>(2 * i + 1, 0) = a21;
		A.at<double>(2 * i, 1) = a12; A.at<double>(2 * i + 1, 1) = a22;
		A.at<double>(2 * i, 2) = a13; A.at<double>(2 * i + 1, 2) = a23;
		A.at<double>(2 * i, 3) = a14; A.at<double>(2 * i + 1, 3) = a24;
		A.at<double>(2 * i, 4) = a15; A.at<double>(2 * i + 1, 4) = a25;
		A.at<double>(2 * i, 5) = a16; A.at<double>(2 * i + 1, 5) = a26;
		A.at<double>(2 * i, 6) = a17; A.at<double>(2 * i + 1, 6) = a27;
		A.at<double>(2 * i, 7) = a18; A.at<double>(2 * i + 1, 7) = a28;
		A.at<double>(2 * i, 8) = a19; A.at<double>(2 * i + 1, 8) = a29;
		A.at<double>(2 * i, 9) = a110; A.at<double>(2 * i + 1, 9) = a210;
		A.at<double>(2 * i, 10) = a111; A.at<double>(2 * i + 1, 10) = a211;
		A.at<double>(2 * i, 11) = a112; A.at<double>(2 * i + 1, 11) = a212;
		A.at<double>(2 * i, 12) = a113; A.at<double>(2 * i + 1, 12) = a213;
		//观测值
		l.at<double>(2 * i, 0) = x - (x0 - f * Xbar / Zbar - delta_x);
		l.at<double>(2 * i + 1, 0) = y - (y0 - f * Ybar / Zbar - delta_y);
	}
}
//---------------------误差方程迭代求解--------------------

void calcu_left(char ctrl_path[],char left_path[])
{
	vector<ControlPoint> ControlPoints;
	vector<imgPoint> left_imgPoints;

	readctrl_ptData(ctrl_path, ControlPoints);
	readImgData(left_path, left_imgPoints);

	//定义两张相片的内外方位元素
	orienParam left_orien;
	left_orien.x0 = 0;
	left_orien.y0 = 0;
	left_orien.f = 27;
	left_orien.Xs = 1500;
	left_orien.Ys = -200;
	left_orien.Zs = -1000;
	left_orien.Kappa = 0;
	left_orien.Omega = 0;
	left_orien.Phi = 0.3;
	left_orien.k1 = 0;
	left_orien.k2 = 0;
	left_orien.p1 = 0;
	left_orien.p2 = 0;

	//将像素坐标(pixel)转换为图像坐标(mm)
	Pixel2Img_with_co_change(left_imgPoints);

	//生成点对
	vector<merge_point> left_merge_points;
	Merge_Point(left_imgPoints, ControlPoints, left_merge_points);

	//构建左片系数阵A和常数项l
	Mat A(2 * left_merge_points.size(), 13, CV_64FC1);
	Mat l(2 * left_merge_points.size(), 1, CV_64FC1);
	Mat X(13, 1, CV_64FC1);
	int i = 0;
	while (true)
	{
		i++;
		printf("%d", i);
		//填充系数阵
		cal_Coefficient(A, l, left_merge_points, left_orien);
		//cout << "L = " << l << endl;
		//最小二乘
		X = (A.t() * A).inv() * A.t() * l;
		//更新外方位元素
		left_orien.Xs += X.at<double>(0, 0);
		left_orien.Ys += X.at<double>(1, 0);
		left_orien.Zs += X.at<double>(2, 0);
		left_orien.Phi += X.at<double>(3, 0);
		left_orien.Omega += X.at<double>(4, 0);
		left_orien.Kappa += X.at<double>(5, 0);
		left_orien.f += X.at<double>(6, 0);
		left_orien.x0 += X.at<double>(7, 0);
		left_orien.y0 += X.at<double>(8, 0);
		left_orien.k1 += X.at<double>(9, 0);
		left_orien.k2 += X.at<double>(10, 0);
		left_orien.p1 += X.at<double>(11, 0);
		left_orien.p2 += X.at<double>(12, 0);
		if (abs(X.at<double>(0, 0)) < 0.0001 && abs(X.at<double>(1, 0)) < 0.0001 && abs(X.at<double>(2, 0)) < 0.0001 &&
			abs(X.at<double>(3, 0)) < 0.0001 && abs(X.at<double>(4, 0)) < 0.0001 && abs(X.at<double>(5, 0)) < 0.0001 &&
			abs(X.at<double>(6, 0)) < 0.0001 && abs(X.at<double>(7, 0)) < 0.0001 && abs(X.at<double>(8, 0)) < 0.0001 &&
			abs(X.at<double>(9, 0)) < 0.0001 && abs(X.at<double>(10, 0)) < 0.0001 && abs(X.at<double>(11, 0)) < 0.0001 &&
			abs(X.at<double>(12, 0)) < 0.0001)
			break;
	}
	//输出定位参数left_orien
	cout << "内外方位元素和畸变系数：" << endl;
	cout << "Xs: " << left_orien.Xs << endl;
	cout << "Ys: " << left_orien.Ys << endl;
	cout << "Zs: " << left_orien.Zs << endl;
	cout << "Phi: " << left_orien.Phi << endl;
	cout << "Omega: " << left_orien.Omega << endl;
	cout << "Kappa: " << left_orien.Kappa << endl;
	cout << "f: " << left_orien.f << endl;
	cout << "x0: " << left_orien.x0 << endl;
	cout << "y0: " << left_orien.y0 << endl;
	cout << "k1: " << left_orien.k1 << endl;
	cout << "k2: " << left_orien.k2 << endl;
	cout << "p1: " << left_orien.p1 << endl;
	cout << "p2: " << left_orien.p2 << endl;
	cout << "----------------------------------" << endl;
	Mat V = A * X - l;
	Mat vtv = V.t() * V;
	double sigma0 = sqrt(vtv.at<double>(0, 0) / (2 * left_merge_points.size() - 13));//单位权中误差
	cout << "单位权中误差: " << endl << sigma0 << "mm" << " or " << sigma0 / PIXSIZE << "pixel" << endl;
	cout << "----------------------------------" << endl;
	//精度统计 --> 各未知数的中误差
	Mat Qxx = (A.t() * A).inv();
	vector<string> str = { "Xs", "Ys", "Zs", "Phi", "Omega", "Kappa", "f", "x0", "y0", "k1", "k2", "p1", "p2" };
	cout << "未知数中误差：" << endl;
	for (int i = 0; i < 13; i++)
	{
		double sigmaXi = sqrt(Qxx.at<double>(i, i)) * sigma0;
		cout << str[i] << ": " << sigmaXi << endl;
	}
	cout << "----------------------------------" << endl;
	//精度统计 --> 单位权中误差
	cout << "像点观测值残差/pixel" << endl;
	cout << "id" << "    vx  " << "	   vy" << endl;
	for (int i = 0; i < left_merge_points.size(); i++)
	{
		cout << left_merge_points[i].flag << "  " << setiosflags(ios::right) << fixed << setprecision(5) << V.at<double>(2 * i, 0) / PIXSIZE << "	" << setiosflags(ios::right) << fixed << setprecision(5) << V.at<double>(2 * i + 1, 0) / PIXSIZE << endl;
	}
}

void calcu_right(char ctrl_path[], char right_path[])
{
	vector<ControlPoint> ControlPoints;
	vector<imgPoint> right_imgPoints;

	readctrl_ptData(ctrl_path, ControlPoints);
	readImgData(right_path, right_imgPoints);

	//定义两张相片的内外方位元素
	orienParam right_orien;
	right_orien.x0 = 0;
	right_orien.y0 = 0;
	right_orien.f = 27;
	right_orien.Xs = 4500;
	right_orien.Ys = 200;
	right_orien.Zs = -1000;
	right_orien.Kappa = 0;
	right_orien.Omega = 0;
	right_orien.Phi = -0.2678;
	right_orien.k1 = 0;
	right_orien.k2 = 0;
	right_orien.p1 = 0;
	right_orien.p2 = 0;

	//将像素坐标(pixel)转换为图像坐标(mm)
	Pixel2Img_with_co_change(right_imgPoints);

	//生成点对
	vector<merge_point> right_merge_points;
	Merge_Point(right_imgPoints, ControlPoints, right_merge_points);

	//构建左片系数阵A和常数项l
	Mat A(2 * right_merge_points.size(), 13, CV_64FC1);
	Mat l(2 * right_merge_points.size(), 1, CV_64FC1);
	Mat X(13, 1, CV_64FC1);
	int i = 0;
	while (true)
	{	
		i++;
		printf("%d", i);
		//填充系数阵
		cal_Coefficient(A, l, right_merge_points, right_orien);
		//cout << "L = " << l << endl;
		//最小二乘
		X = (A.t() * A).inv() * A.t() * l;
		//更新外方位元素
		right_orien.Xs += X.at<double>(0, 0);
		right_orien.Ys += X.at<double>(1, 0);
		right_orien.Zs += X.at<double>(2, 0);
		right_orien.Phi += X.at<double>(3, 0);
		right_orien.Omega += X.at<double>(4, 0);
		right_orien.Kappa += X.at<double>(5, 0);
		right_orien.f += X.at<double>(6, 0);
		right_orien.x0 += X.at<double>(7, 0);
		right_orien.y0 += X.at<double>(8, 0);
		right_orien.k1 += X.at<double>(9, 0);
		right_orien.k2 += X.at<double>(10, 0);
		right_orien.p1 += X.at<double>(11, 0);
		right_orien.p2 += X.at<double>(12, 0);
		if (abs(X.at<double>(0, 0)) < 0.0001 && abs(X.at<double>(1, 0)) < 0.0001 && abs(X.at<double>(2, 0)) < 0.0001 &&
			abs(X.at<double>(3, 0)) < 0.0001 && abs(X.at<double>(4, 0)) < 0.0001 && abs(X.at<double>(5, 0)) < 0.0001 &&
			abs(X.at<double>(6, 0)) < 0.0001 && abs(X.at<double>(7, 0)) < 0.0001 && abs(X.at<double>(8, 0)) < 0.0001 &&
			abs(X.at<double>(9, 0)) < 0.0001 && abs(X.at<double>(10, 0)) < 0.0001 && abs(X.at<double>(11, 0)) < 0.0001 &&
			abs(X.at<double>(12, 0)) < 0.0001)
			break;
	}
	//输出定位参数right_orien
	cout << "内外方位元素和畸变系数：" << endl;
	cout << "Xs: " << right_orien.Xs << endl;
	cout << "Ys: " << right_orien.Ys << endl;
	cout << "Zs: " << right_orien.Zs << endl;
	cout << "Phi: " << right_orien.Phi << endl;
	cout << "Omega: " << right_orien.Omega << endl;
	cout << "Kappa: " << right_orien.Kappa << endl;
	cout << "f: " << right_orien.f << endl;
	cout << "x0: " << right_orien.x0 << endl;
	cout << "y0: " << right_orien.y0 << endl;
	cout << "k1: " << right_orien.k1 << endl;
	cout << "k2: " << right_orien.k2 << endl;
	cout << "p1: " << right_orien.p1 << endl;
	cout << "p2: " << right_orien.p2 << endl;
	cout << "----------------------------------" << endl;
	Mat V = A * X - l;
	Mat vtv = V.t() * V;
	double sigma0 = sqrt(vtv.at<double>(0, 0) / (2 * right_merge_points.size() - 13));//单位权中误差
	cout << "单位权中误差: " << endl << sigma0 << "mm" << " or " << sigma0 / PIXSIZE << "pixel" << endl;
	cout << "----------------------------------" << endl;
	//精度统计 --> 各未知数的中误差
	Mat Qxx = (A.t() * A).inv();
	vector<string> str = { "Xs", "Ys", "Zs", "Phi", "Omega", "Kappa", "f", "x0", "y0", "k1", "k2", "p1", "p2" };
	cout << "未知数中误差：" << endl;
	for (int i = 0; i < 13; i++)
	{
		double sigmaXi = sqrt(Qxx.at<double>(i, i)) * sigma0;
		cout << str[i] << ": " << sigmaXi << endl;
	}
	cout << "----------------------------------" << endl;
	//精度统计 --> 单位权中误差
	cout << "像点观测值残差/pixel" << endl;
	cout << "id" << "    vx  " << "	   vy" << endl;
	for (int i = 0; i < right_merge_points.size(); i++)
	{
		cout << right_merge_points[i].flag << "  " << setiosflags(ios::right) << fixed << setprecision(5) << V.at<double>(2 * i, 0) / PIXSIZE << "	" << setiosflags(ios::right) << fixed << setprecision(5) << V.at<double>(2 * i + 1, 0) / PIXSIZE << endl;
	}
}
//------------------------主函数------------------------

int main()
{
	//读取控制点数据和左右片标志点的像素坐标
	
	
	char ctrl_ptfile[] = "C:/Users/LENOVO/Desktop/近景摄影测量/2024实习_近景控制场_20240515.txt";
	//char left_file[] = "C:/Users/LENOVO/Desktop/近景摄影测量/coordinates.txt";
	//char right_file[] = "C:/Users/LENOVO/Desktop/近景摄影测量/coordinates_right.txt";
	char left_file[] = "C:/Users/LENOVO/Desktop/近景摄影测量/datapt/points_imgL.txt";
	char right_file[] = "C:/Users/LENOVO/Desktop/近景摄影测量/datapt/points_imgR.txt";
	printf("-----------左片-----------------\n");
	calcu_left(ctrl_ptfile,left_file);
	printf("-----------右片-----------------\n");
	calcu_right(ctrl_ptfile, right_file);
	

	
	return 0;
}

// 运行程序: Ctrl + F5 或调试 >“开始执行(不调试)”菜单
// 调试程序: F5 或调试 >“开始调试”菜单

// 入门使用技巧: 
//   1. 使用解决方案资源管理器窗口添加/管理文件
//   2. 使用团队资源管理器窗口连接到源代码管理
//   3. 使用输出窗口查看生成输出和其他消息
//   4. 使用错误列表窗口查看错误
//   5. 转到“项目”>“添加新项”以创建新的代码文件，或转到“项目”>“添加现有项”以将现有代码文件添加到项目
//   6. 将来，若要再次打开此项目，请转到“文件”>“打开”>“项目”并选择 .sln 文件

三、单片空间后方交会结果与分析

在这一步我设立了两组数据运行计算，分别利用81(左）/63（右）对控制点和9（左）/19（右）对控制点进行控制计算。

3.1未知数求解结果

表1 未知数求解结果

未知数	81左片	9左片	63右片	19右片
Xs	1480.28	1468.2	3734.31588	3733.75331
Ys	-61.0423	-63.0068	-63.01434	-66.35926
Zs	-1569.29	-1565.43	-1439.08581	-1421.84848
Phi	0.380894	0.386272	-0.27555	-0.26203
Omega	-0.0746003	-0.0756672	-0.06311	-0.05947
Kappa	-0.0222901	-0.0222292	-0.02232	-0.02173
f	28.0798	28.2235	27.94212	28.07034
x0	0.153123	0.227625	-0.06787	0.26542
y0	-0.0704426	-0.119314	-0.08808	-0.01218
k1	2.78244e-05	0.000144189	0.00006	0.00009
k2	6.55726e-08	-1.12597e-06	-0.00000	-0.00000
p1	-0.000103156	-0.000236663	0.00003	-0.00022
p2	1.41688e-05	1.1339e-05	0.00002	-0.00006

3.2精度统计-中误差

表2 中误差

未知数	81左片	9左片	63右片	19右片
$\sigma 0$ /mm	0.0084879	0.00189872	0.00549	0.00233
Xs	1.31468	8.51379	0.99255	1.14192
Ys	0.763872	2.39405	0.66409	0.97752
Zs	2.6982	23.6963	2.55542	5.26219
Phi	0.00264403	0.00483118	0.00210	0.00198
Omega	0.00156104	0.00297731	0.00139	0.00152
Kappa	0.000203308	0.000290429	0.00014	0.00012
f	0.0243822	0.188117	0.02080	0.04314
x0	0.0734404	0.145106	0.05773	0.05455
y0	0.0432928	0.0890243	0.03780	0.03927
k1	1.22928e-05	3.4379e-05	0.00001	0.00001
k2	6.32626e-08	4.50327e-07	0.00000	0.00000
p1	3.40386e-05	5.49139e-05	0.00003	0.00003
p2	2.11434e-05	3.7823e-05	0.00002	0.00002

3.3精度统计-像点量测残差

第一组81左片/63右片结果（单位/pixel）：

表3 像点量测残差

左片点号	x残差	y残差	右片点号	x残差	y残差
433	-0.62095	0.13756	310	-1.61662	0.15782
432	-1.74451	-0.33490	311	-1.65273	-0.03667
431	-1.57404	-0.88220	404	0.28651	0.32884
430	-0.64663	-1.14805	403	0.22159	0.07376
336	4.10305	1.22820	402	0.40321	-0.28741
335	-2.75036	-13.00877	215	1.02983	-0.13605
334	2.64072	0.36014	214	1.05181	-0.32796
333	2.41191	-0.46022	213	1.17226	0.07413
332	1.11780	12.39554	212	0.88652	0.10367
331	3.15618	0.04941	211	1.12198	0.56216
330	4.12387	-0.22648	210	1.53278	0.72635
444	0.60272	1.37030	414	0.02529	0.47771
443	-0.23673	0.09315	413	0.03613	0.10312
442	-1.13555	-0.33010	412	-0.09874	-0.12480
440	-0.63237	-0.76098	411	0.07119	-0.39951
136	-2.11843	0.74448	325	-0.17913	0.07580
135	-2.89531	0.15862	324	-0.66040	0.05828
134	-3.22999	0.42433	323	-0.83549	0.17139
133	-3.29503	-0.17951	322	-0.80437	0.09284
132	-3.09568	0.08364	321	-0.35824	0.01338
453	-0.88193	0.17537	320	-0.03015	0.68011
452	-0.65304	-0.48186	136	-2.25057	-0.26022
451	-0.80316	-0.36406	135	-2.53939	0.21181
450	-0.76020	-0.29134	133	-3.17127	0.01906
224	1.52084	0.40592	132	-2.26306	0.82028
223	2.14544	-0.91089	336	1.91394	1.14509
463	-0.11589	-0.61793	335	-3.01975	-10.80008
462	0.16913	-1.13554	334	1.79462	1.10271
461	0.07715	0.88509	330	2.08414	-0.52604
460	-0.29776	-0.39359	224	1.24655	0.79333
146	1.78857	0.13480	223	1.85110	-0.52165
145	0.79470	-1.26319	444	-0.06183	1.48511
144	0.26271	-1.34149	443	0.13676	0.08278
143	-0.04321	1.51644	442	0.56908	-0.43631
142	0.69686	1.16097	441	0.46921	0.77800
141	1.92899	0.76305	146	0.68535	0.78576
474	0.78046	0.42144	145	0.84569	-0.43364
473	-0.68182	-0.78100	144	0.75879	-0.39842
472	-1.80948	-1.36192	143	0.65972	1.38616
471	-1.88643	0.64618	141	1.23218	1.48388
470	-0.28885	-0.25348	346	-1.97358	0.68904
356	2.60846	0.46893	345	-1.85002	1.12666
355	2.13113	0.12746	344	-2.03743	-0.16791
354	0.35235	-0.56942	341	-1.81012	1.11004
353	-0.31778	-1.14439	340	-0.73490	0.61732
352	-0.60365	0.37041	453	0.41776	0.41752
351	0.05741	0.74650	452	-0.62342	-0.47697
350	2.88141	-1.32786	451	-0.17934	0.46867
484	1.16442	0.25661	450	0.94827	-0.75538
483	0.09229	0.06645	463	0.55684	0.44397
482	-1.70831	-0.78474	460	0.07882	0.31811
481	-1.77769	-0.15765	156	-0.52812	-1.24965
480	0.09904	-0.89155	155	-0.22708	-0.82278
156	1.46885	-0.23315	356	0.92845	-0.36385
155	0.17655	-0.47601	355	1.03540	-0.57469
154	0.22224	0.15310	354	1.26388	-0.13377
153	0.05616	0.04002	353	1.93696	0.41072
152	-0.13849	0.30598	352	1.90560	0.41165
365	2.09570	0.17810	474	-0.62630	-0.43816
364	1.03931	-0.02909	473	-0.33119	-0.42915
504	1.76054	0.61336	472	-0.15612	-0.28829
503	0.40505	-0.27191	471	-0.09200	0.03536
502	-0.81404	0.53433	470	-0.44685	0.54694
501	-0.37033	-0.38926
514	1.24532	0.59151
512	0.50862	-0.31846
511	0.51372	-0.80161
510	1.14079	-1.02934
375	-0.93836	0.29956
374	-1.76864	0.12483
373	-1.48539	13.58485
372	-2.59171	-0.75417
371	-1.77049	-0.72716
370	-1.18541	-1.05700
166	0.31974	-0.72051
165	-0.41795	-0.58058
164	-0.54549	-0.40483
163	-0.36945	-0.52229
162	0.15837	-0.54022
161	0.18199	-1.35793

第二组9左片/19右片结果（单位/pixel）：

表4 像点量测残差

左片点号	x残差	y残差	右片点号	x残差	y残差
135	-0.04707	-0.21176	215	0.10675	0.58274
134	-0.20008	0.06572	214	-0.01231	-0.62148
133	0.09252	0.01435	213	-0.10637	-0.44505
224	0.55707	0.07368	212	-0.29370	-0.24348
222	-0.35796	-0.42383	211	0.59302	0.26874
144	0.19882	-0.10329	136	0.16293	-0.49429
143	0.03227	0.44675	135	-0.55786	-0.51933
155	-0.05753	0.41565	133	-1.62403	0.21016
153	-0.21803	-0.27728	132	-0.33377	0.77563
			224	0.74483	-0.12368
			223	-0.01780	-0.26971
			146	0.25347	0.01180
			145	0.82920	-0.46231
			144	0.00581	-0.16244
			143	0.14427	0.60631
			156	0.71564	-0.37473
			155	-0.76909	0.57903
			354	0.06517	0.29899
			352	0.09385	0.38309

四、误差剔除

观察表1未知数求解结果，可以发现，使用较少的控制点和较多的控制点得到的结果相差较大，外方位元素可相差数十毫米，但整体解求结果无明显错误。

观察表2可知，利用较少的控制点得到的结果误差较明显，例如Zs中误差，使用较少控制点得到的中误差达到了23.6963mm，而使用较多控制点得到的中误差减小到了2.6982mm。使用较多控制点计算得到的结果虽然误差明显下降且误差较小，外方位元素中误差可达到2~3mm以内，像点量测单位权中误差控制在了亚像素级别，但是像点量测单位权中误差却比使用较少控制点得到的误差大，我认为是较多的控制点中有一些量测误差过大的点。

观察表3、4可以看出，两组实验得到的像点观测值残差都能基本保持在一个像素以内，而且正如上述观点，使用较多的控制点计算时，有许多像点量测误差过大的点，存在明显的量测错误，需要剔除或修改，否则影响整体精度。例如左片的：432、332、335、373、143号点，右片的：335、135、136、133号点，他们的量测误差达到了2~3个像元，尤其是335号点达到了数十个像元。

我通过剔除与重新量测这些点来解决这个问题,剔除这些点后，单位权中误差减小到了和使用较少控制点相近的误差值，且所有未知数的误差值均有所下降，达到较为理想的结果。

表5 剔除粗差前后中误差

未知数	81左片	剔除后左片	63右片	剔除后右片
$\sigma 0$ /mm	0.0084879	0.0024506	0.00549	0.00213
Xs	1.31468	0.58721	0.99255	0.55265
Ys	0.763872	0.326306	0.66409	0.39534
Zs	2.6982	1.1931	2.55542	1.53021
Phi	0.00264403	0.00123878	0.00210	0.00120
Omega	0.00156104	0.000752514	0.00139	0.00080
Kappa	0.000203308	9.35626e-05	0.00014	0.00008
f	0.0243822	0.0107238	0.02080	0.01171
x0	0.0734404	0.0344217	0.05773	0.03311
y0	0.0432928	0.0210118	0.03780	0.02168
k1	1.22928e-05	5.32986e-06	0.00001	0.00001
k2	6.32626e-08	2.78141e-08	0.00000	0.00000
p1	3.40386e-05	1.58742e-05	0.00003	0.00002
p2	2.11434e-05	9.89134e-06	0.00002	0.00001

最终得到的未知数结算结果为（其他未知数变化微小，在上述表中已经展示过，此处不再重复，仅展示外方位线元素）：

表6 剔除误差前后未知数结果（单位/mm）

未知数	81左片	剔除后左片	63右片	剔除后右片
Xs	1480.28	1479.45	3734.31588	3733.87481
Ys	-61.0423	-60.9722	-63.01434	-63.01913
Zs	-1569.29	-1566.85	-1439.08581	-1443.43854

五、误差来源分析

经过误差剔除与重新测量（手动平移对准点）后的结果达到了较为理想的值，我将粗差较大的点记录下来，返回到像点量测程序中去再次框选查看，发现这些粗差点有一些规律：

位于影像边缘或倾斜程度较大，呈现椭圆形或变形。
标志点受光照射，有反光。
像点量测程序定位点存在明显偏差，需要手动调整

所以像点量测程序其实也有待优化，可以使用其他的算法对抗这些存在的问题。

六、误差影响分析

若手动加入一个很大的粗差，究竟会对整体求解造成哪些影响？我将后方交会程序中的左片的433号点的x坐标从41.38改到1000，手动加入了一个非常大的粗差，运行代码，发现会造成以下问题：

迭代次数变多：从18次增加到了47次收敛
未知数计算值明显变化：

表7 加入粗差前后未知数值

未知数	后方交会	加入粗差
Xs	1480.28	1569.57
Ys	-61.0423	-70.1796
Zs	-1569.29	-1710.93

3.统计误差变大

表8 加入粗差前后中误差

未知数	误差值	未知数	误差值
$\sigma 0$ /pixel	73.34	y0	1.6432928
Xs	46.9177	k1	0.000340061
Ys	25.5392	k2	8.70585e-07
Zs	91.357	p1	0.00104376
Phi	0.08264403	p2	0.000760362
Omega	0.06456104
Kappa	0.008203308
f	0.8243822
x0	2.1734404

像点量测残差变大，且带动周围点残差变大

表9 加入粗差前后像点量测残差

像点号左	x残差/mm	y残差/mm
433	-763.86253	-10.21276
431	37.21429	16.95733
444	86.36103	-21.28834
443	103.39708	-7.70386
442	94.48565	16.12521
440	2.89685	13.26422
136	23.68336	2.66507
135	33.94583	6.55190
134	27.81508	16.64054
133	-3.13424	18.49584
453	77.65230	-20.22846
452	71.50186	11.07310
451	46.72870	31.99060
450	4.75211	25.33406
224	27.32684	-17.38990
223	26.81550	3.32593
463	43.51226	-25.44046
462	39.26717	6.16854