排序算法之归并排序

归并排序

        归并排序是利用归并的思想实现的排序方法，该算法采用经典的分治的策略。

        下图就是我们归并排序的整体流程，有一个划分的过程，也有一个合并的过程，在合并的时候，会按照数字大小依次排序。我们每进行依次划分，都要进行合并排序。

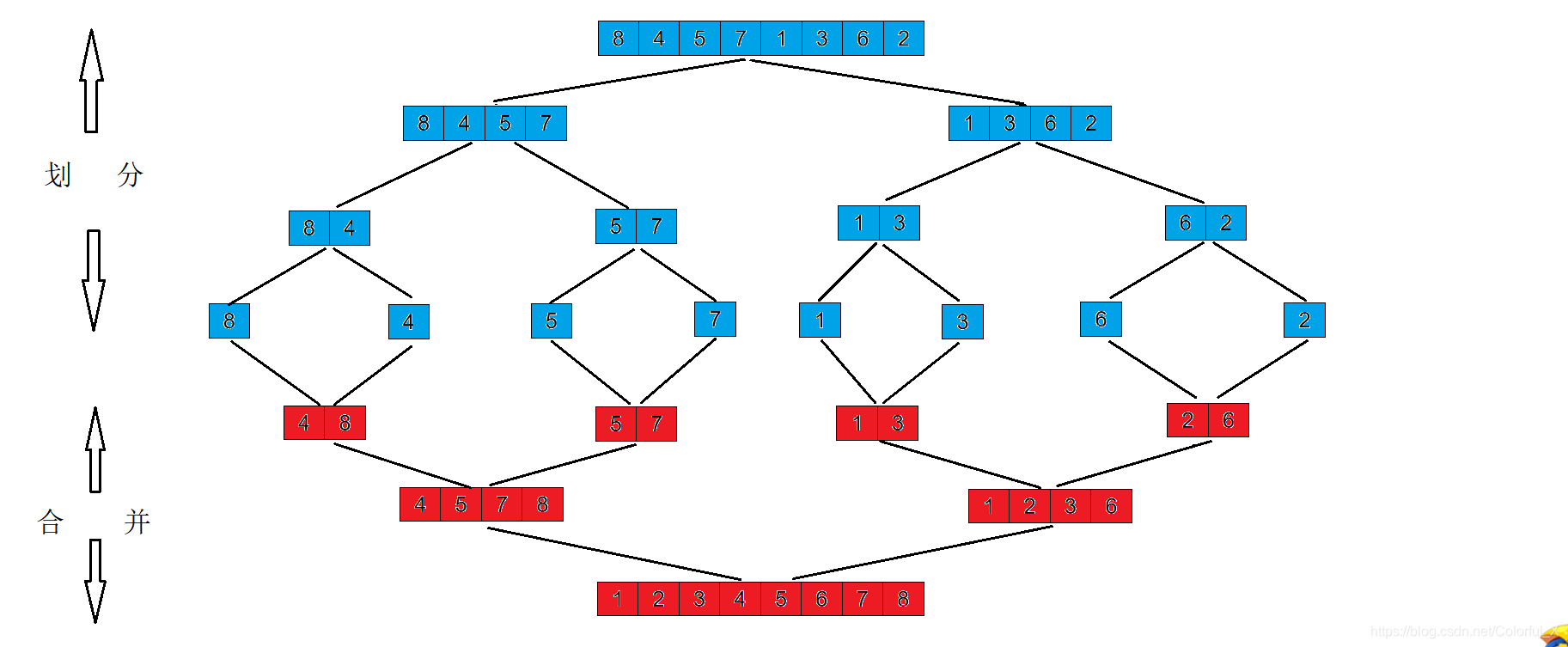
        我们下面通过图示，来演示是怎么进行合并的，以上述图中， {4,5,7,8}和{1,2,3,6}这两个有序序列举例来说明合并的过程：

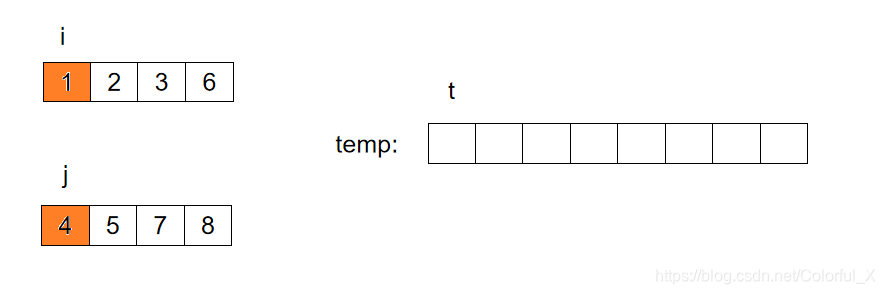
        合并两个数组，我们需要借助一个临时的数组temp，用来存放合并以后的数据。如下图所示：

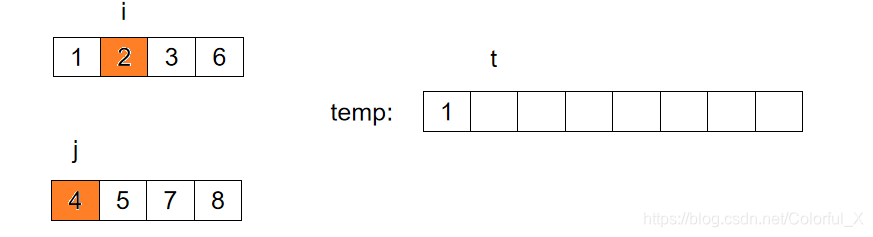
        比较 i 和 j 位置上的数据，如果 i 指向的数据 小于 j 指向的数据，则将 i 指向的数据放入temp中，通过 i++，t++。如下图：

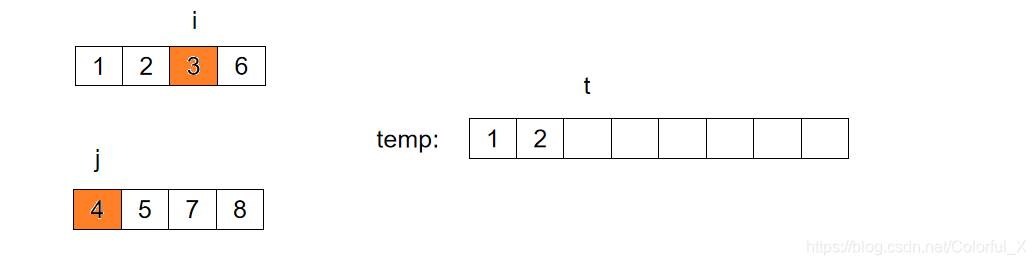
        同理，继续比较，如下图所示：

        继续比较，如图所示：

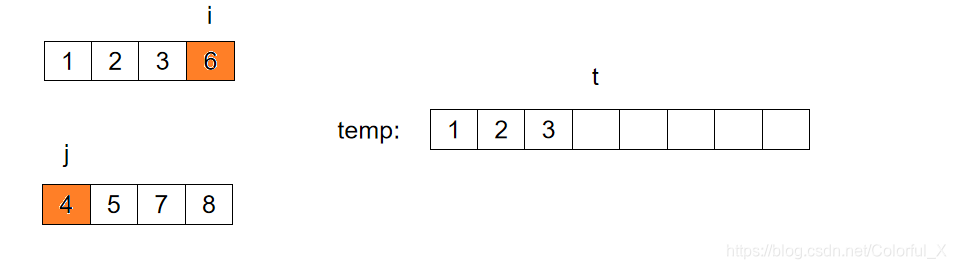
         比较后，如上图所示，此时 i 指向的数据为6，j指向的数据为4， 所以将 j 指向的数据放入temp中，并将 j++，如下图：

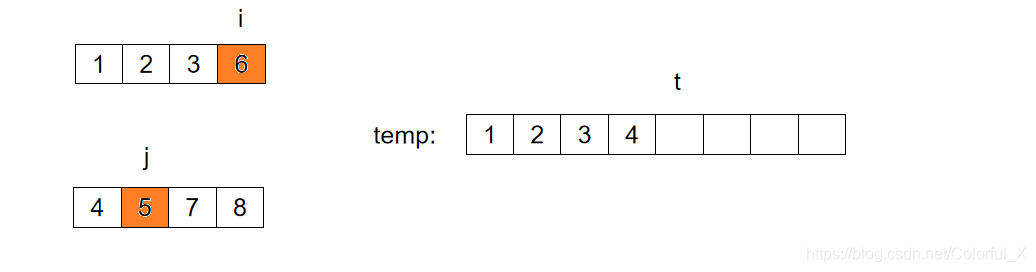
        继续比较：

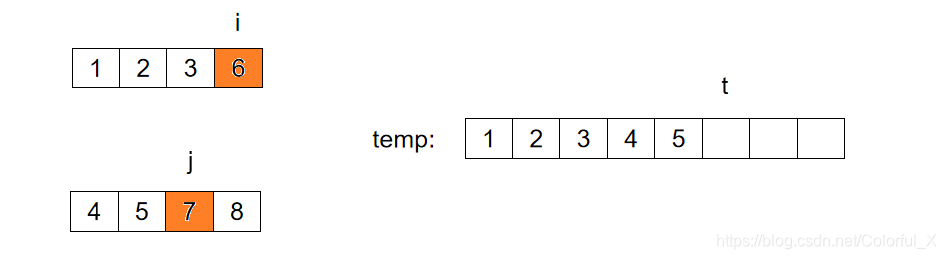
        此时，i 指向的数据为6，j 指向的数据为7。我们又要将 i 指向的数据 放入temp中，并将 i++， t++。

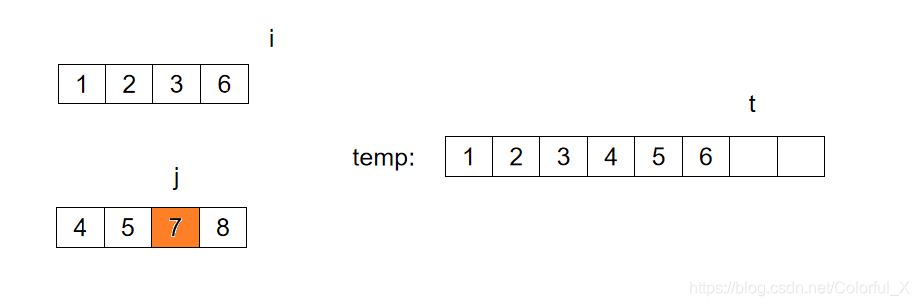
        此时，i已经超过了数组的范围，所以，我们无需再比较i 和 j 谁指向的值大了，我们可以直接将j指向的数据以及j之后的数据全部依次放入到temp中，如下图：
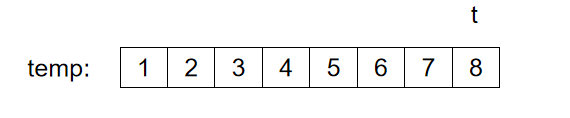        此时，我们得到的temp数组，就是一个有序的数组了。

        特别注意：上述过程只是最后一次合并的过程，在整个归并排序中，我们每拆分一次，对应的就要合并一次。而且，我们是将已经排好序的元素放在临时数组中，所以还需要将临时数组中的数据又拷贝回原数组中。

代码实现：

    /**
     * 合并的过程
     * @param ar ：待排序的数组
     * @param left：待排序数组的初始位置
     * @param mid：中间位置
     * @param right：终止位置
     * @param temp：临时数组
     */
    public static void mergeSort(int[]ar,int left,int mid,int right,int[]temp){
        int i = left;
        int j = mid+1;
        int t = 0;
        // 合并的过程
        while(i<=mid && j<=right){
            if (ar[i] >= ar[j]){
                temp[t++] = ar[j++];
            }else{
                temp[t++] = ar[i++];
            }
        }

        while(i<=mid){
            temp[t++] = ar[i++];
        }

        while(j<=right){
            temp[t++] = ar[j++];
        }

        // 拷贝回原数组
        t = 0;
        int tempLeft = left;
        while(tempLeft<=right) {
            ar[tempLeft++] = temp[t++];
        }

    }

//不断地划分数组，分一次 就要 合并一次
    public static void merge(int[]ar,int left,int right){
        int [] temp = new int[ar.length];
        if (left<right) {
            int mid = (left + right) / 2;
            merge(ar, left, mid);
            merge(ar, mid + 1, right);
            mergeSort(ar, left, mid, right, temp);
        }
    }