石子合并多种解法

线性朴素n^3

using ll = long long;

int dp1[305][305], dp2[305][305];
int main() {
	int n;
	std::cin >> n;
	std::vector<int>a(n + 1), sum(n + 1);
	//扩增,计算前缀和
	for (int i = 1; i <= n; i++) {
		std::cin >> a[i];
		sum[i] = sum[i - 1] + a[i];
	}
	//i是区间
	for (int i = 1; i < n; i++) {
		//j是左端点
		for (int j = 1; j + i <= n; j++) {
			//e是右端点
			int e = i + j;
			dp1[j][e] = 1e9;
			dp2[j][e] = -1;
			//k是分隔点
			for (int k = j; k + 1 <= e; k++) {
				dp1[j][e] = std::min(dp1[j][e], dp1[j][k] + dp1[k + 1][e] + sum[e] - sum[j - 1]);
				dp2[j][e] = std::max(dp2[j][e], dp2[j][k] + dp2[k + 1][e] + sum[e] - sum[j - 1]);
			}

		}
	}
	std::cout << dp1[1][n] << '\n' << dp2[1][n];
	return 0;
}

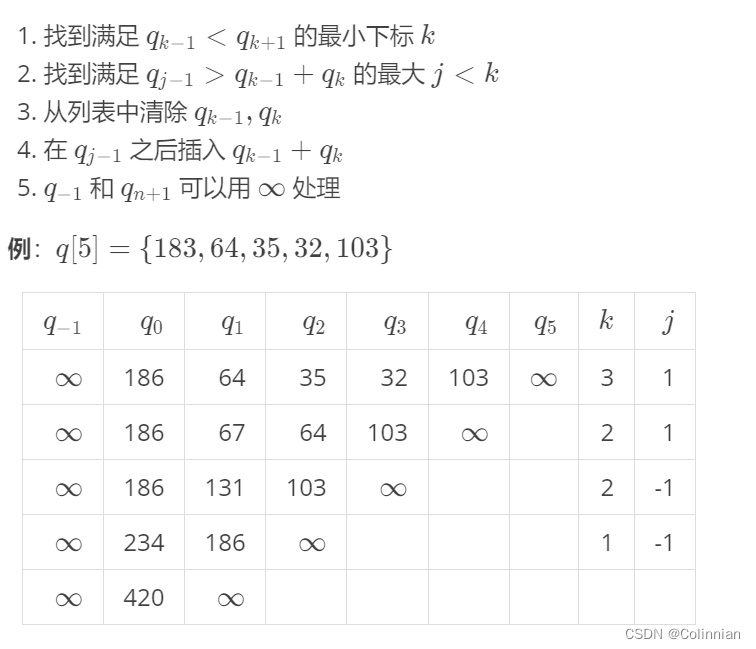
nlogn解法

int n, k, j;
int ans, sum;

int main()
{
    std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
    std::cin >> n;
    std::vector<int>v(n + 2);
    v[0]=INT_MAX - 1,v[n + 1] = INT_MAX;
    for (int i = 1; i <= n; i++)std::cin >> v[i];

    while (n > 1)
    {
        //第一步找到最小的k-1<k+1的项
        for (k = 1; k <= n; k++)
            if (v[k - 1] < v[k + 1])
                break;
        //sum+v[k]+v[k-1]
        sum = v[k] + v[k - 1];
        //第二步找到满足j>k+k-1的最大j且j<=k-1
        for (j = k - 1; j >= 0; j--)
            if (v[j] > v[k] + v[k - 1])
                break;
        //从列表中清除k-1和k
        v.erase(v.begin() + k - 1);
        v.erase(v.begin() + k - 1);
        //在j+1后插入sum
        v.insert(v.begin() + j + 1, sum);
        //答案加上sum
        ans += sum;
        n--;
    }

    printf("%d", ans);
    return 0;
}

 环型石子合并n^3

using ll = long long;

int dp1[205][205], dp2[205][205];
int main() {
	int n;
	std::cin >> n;
	std::vector<int>a(2 * n + 1), sum(2 * n + 1);
	//扩增,计算前缀和
	for (int i = 1; i <= 2 * n; i++) {
		if (i <= n) {
			std::cin >> a[i];
			a[i + n] = a[i];
		}
		sum[i] = sum[i - 1] + a[i];
	}
	//i是区间
	for (int i = 1; i < n; i++) {
		//j是左端点
		for (int j = 1; j + i <= 2 * n; j++) {
			//e是右端点
			int e = i + j;
			dp1[j][e] = 1e9;
			dp2[j][e] = -1;
			//k是分隔点
			for (int k = j; k + 1 <= e; k++) {
				dp1[j][e] = std::min(dp1[j][e], dp1[j][k] + dp1[k + 1][e] + sum[e] - sum[j - 1]);
				dp2[j][e] = std::max(dp2[j][e], dp2[j][k] + dp2[k + 1][e] + sum[e] - sum[j - 1]);
			}

		}
	}
	int min_val = 1e9, max_val = 0;
	for (int i = 1; i <= n; i++) {
		min_val = std::min(min_val, dp1[i][i + n - 1]);
		max_val = std::max(max_val, dp2[i][i + n - 1]);
	}
	std::cout << min_val << '\n' << max_val;
	return 0;
}