算法实习笔记——DBSCAN聚类算法

DBSCAN聚类算法

DBSCAN是基于密度的带噪声应用的空间聚类算法。

DBSCAN 是通过点的密度来识别聚类集群。聚类通常位于高密度区域，而异常值往往位于低密度区域。使用该算法的 3 个主要优势（根据该算法的先驱者的说法）是：它只需要最少的领域知识，可以发现任意形状的聚类，并且对于大型数据库来说非常高效

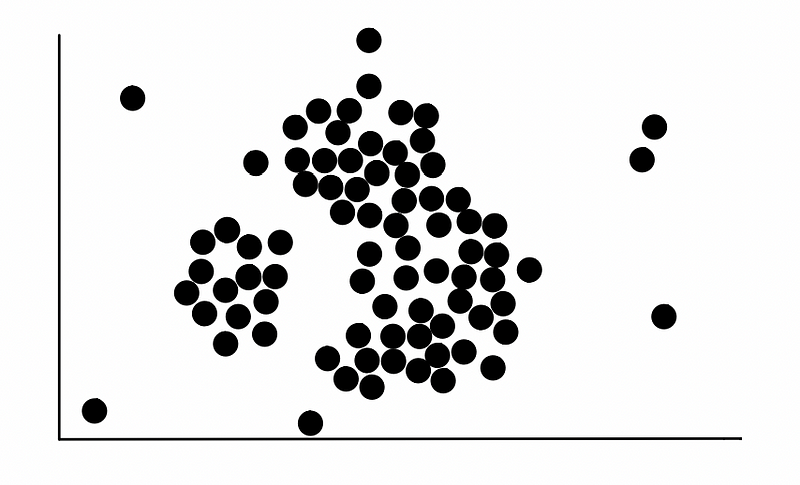
如上图所示是一个数据集，有众多的离散点，其中每一点都代表一个样本。

1.中心圆探测半径

设置eps参数，对于每一个样本点进行中心元探测，探测圆内其他样本点的个数，如下图所示。

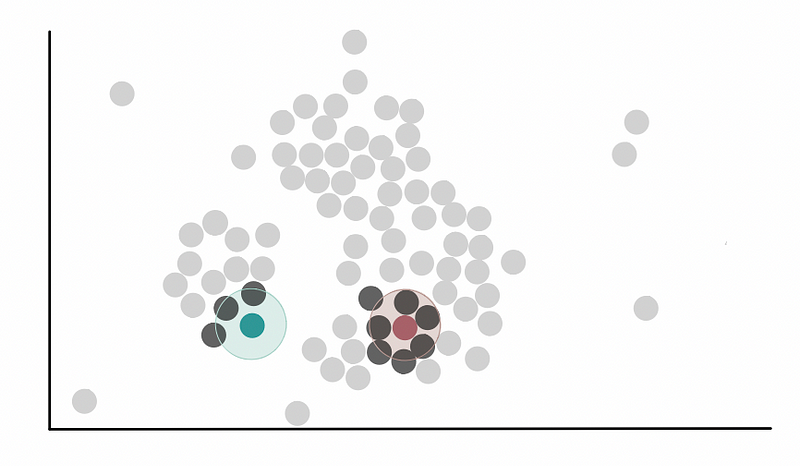
左侧绿色小圈的中心点的中心圆内有三个样本点，而右侧红色小圈的中心点的中心圆内有七个样本点，

2.核心点和非核心点

设置第二个参数minPoints，我们认定当某个中心点的中心圆内样本点数目少于minPoints，则该点定义为非核心点，反之则为核心点。

一般来说，minPoints ≥数据集的维数+ 1。对于有噪声的数据集来说，较大的值通常更好。minPoints 的最小值必须是 3，但数据集越大，minPoints 值就必须越大。

通过划分核心点和非核心点，大概如下图所示：

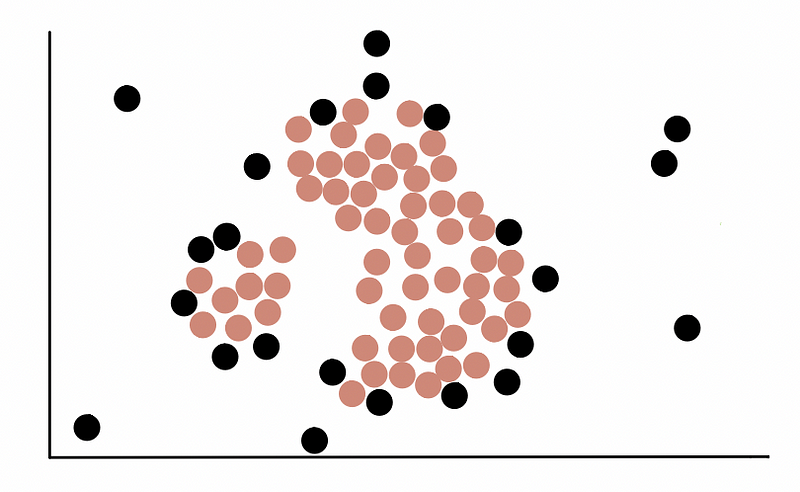
3.群组划分

while(未分配标签的核心点不为空)
{
	随机选取一个核心点加入队列q.push(x)，为其分配群组名
	while(!q.empty())
	{
        将队首中心圆内的所有点（包括核心点和非核心点）分配同一群组名
        q.pop();
        q.push(队首中心圆内的其余核心点)//加入队列
	}
}

注意到，我们不会扩散非核心点中心圆内的其他非核心点，只针对核心点的中心圆内的所有点进行扩散命名

群组划分结果如下：

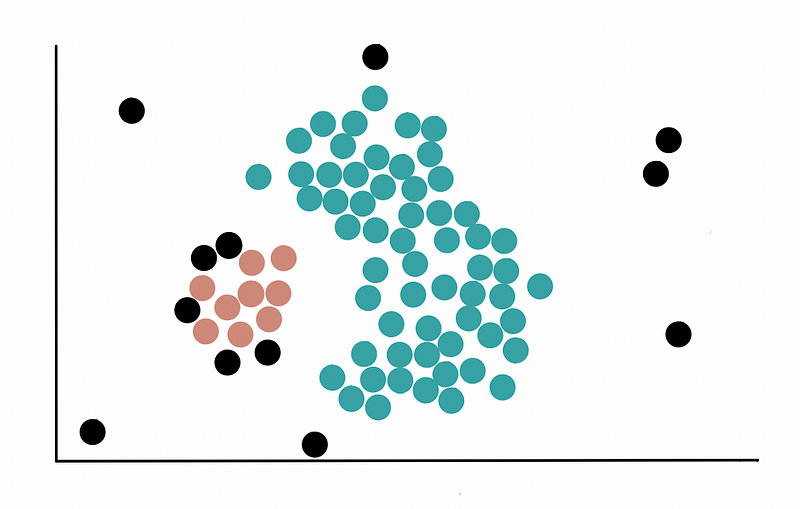
其中红色是还未划分的点，所以会进行第二轮划分，最终结果如下：

就这样，我们完成了DBSCAN的2个群组集群聚类，并发现了7个异常离群值。

知识扩展：聚类算法

一、DBSCAN vs K-means

对比维度	K-means	DBSCAN
核心思想	基于距离，最小化簇内方差	基于密度，寻找高密度区域
是否需要指定簇数	✅ 需要预设 K 值	❌ 自动确定
簇的形状	只能识别球形/凸形簇	可识别任意形状
能否识别噪声	❌ 所有点必须归类	✅ 能标记离群点为噪声
对异常值敏感度	高（会拉偏中心点）	低（异常值标记为噪声）
计算复杂度	O(n·k·t) 较快	O(n²) 或 O(n log n)

图示对比

数据分布：                K-means结果：           DBSCAN结果：

  ****                    ****                    ****
 ******      ···         ██████      ███         ██████      ···
  ****       ···          ████       ███          ████       噪声
             ···                     ███                     
    ▲▲▲                    ▲▲▲                    ▲▲▲
   ▲▲▲▲▲                  ▲▲▲▲▲                  ▲▲▲▲▲
    ▲▲▲                    ▲▲▲                    ▲▲▲

                         (错误地把噪声           (正确识别3个簇
                          归入某个簇)             + 噪声点)

二、常见聚类算法全览

算法	类型	优点	缺点	适用场景
K-means	划分式	快速、简单、可扩展	需预设K，只能球形簇，对异常值敏感	大数据、簇大小均匀
DBSCAN	密度式	自动确定簇数，识别噪声，任意形状	对密度不均匀敏感，参数敏感	噪声多、形状不规则
层次聚类	层次式	可视化树状图，不需预设K	计算慢O(n³)，不可逆	小数据、需要层次结构
GMM	概率式	软聚类（概率归属），椭圆形簇	需预设K，计算较慢	簇有重叠、需要概率
OPTICS	密度式	DBSCAN改进，适应不同密度	更复杂，需要后处理	密度不均匀
Mean Shift	密度式	自动确定簇数，无需预设	计算慢，带宽敏感	图像分割
谱聚类	图论式	处理复杂形状，效果好	计算慢，需预设K	图结构、复杂形状

三、算法选择依据判断

需要预设簇数？
├─ 是 → 簇形状规则？
│       ├─ 是 → K-means
│       └─ 否 → 谱聚类 / GMM
│
└─ 否 → 数据有噪声？
        ├─ 是 → 密度均匀？
        │       ├─ 是 → DBSCAN
        │       └─ 否 → OPTICS
        └─ 否 → 层次聚类 / Mean Shift

参考文献：
一文弄懂DBSCAN聚类算法 - 知乎