Leetcode Hot100|84. 柱状图中最大的矩形 Python

最新推荐文章于 2025-12-28 22:03:12 发布

原创最新推荐文章于 2025-12-28 22:03:12 发布 · 361 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法

Algorithm 专栏收录该内容

18 篇文章

订阅专栏

本文分享了一道较难的编程题的解题思路及代码实现。该问题通过使用单调栈来解决最大矩形面积的问题，并引入哨兵简化边界条件处理。文章详细解释了算法逻辑并提供了Python代码。

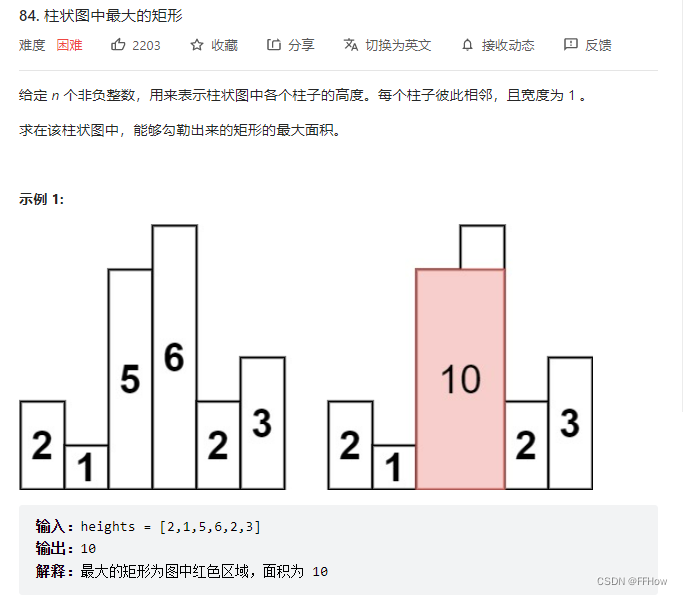
在这里插入图片描述
这题目挺难的，尽管知道是在考察单调栈，但没看题解前也没做出来。主要是要想清楚一个东西，我们是在对不同的高度搜索，也就是针对每个特定的高度进行宽度扩展，而这个扩展的过程正好符合单调栈的特性。

同时，这个题还有很多边界情况需要考虑，为了回避，我们引用了哨兵，让代码大大简化。带有注释的代码如下。

class Solution(object):
    def largestRectangleArea(self, heights):
    
        stack = [0]   #0作为哨兵，这样栈不会为空，少一些判断。
        max_area = 0

        heights = [0] + heights + [0]    #加哨兵。头部那个是为了占位，尾部0是确保所有元素都会弹出。

        for i in range(1, len(heights)):
            # print(stack)
            while heights[i] < heights[stack[-1]]:  #当前元素小于栈顶元素对应的高度
                item = stack.pop() 		#弹出栈顶
                area_new = heights[item] * (i - stack[-1] - 1)  #弹出来的元素对应高度的最大面积（注意是宽度是减1）
                max_area = max(max_area, area_new)

            stack.append(i)   #压入栈

        return max_area