Leetcode Hot100|85.最大矩形 Python

最新推荐文章于 2025-09-08 09:22:18 发布

原创最新推荐文章于 2025-09-08 09:22:18 发布 · 387 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #python #算法

Algorithm 专栏收录该内容

18 篇文章

订阅专栏

本文详细介绍了两种方法解决寻找二维矩阵中最大矩形面积的问题。方法一是利用动态规划思想，计算每行到某个元素的连续1的数量，再遍历矩阵找出最大面积；方法二是通过调整矩阵，结合栈结构快速找到最大矩形。这两种方法都展示了在算法设计上的巧妙之处。

在这里插入图片描述
题目描述很简单，我们来看看示例。

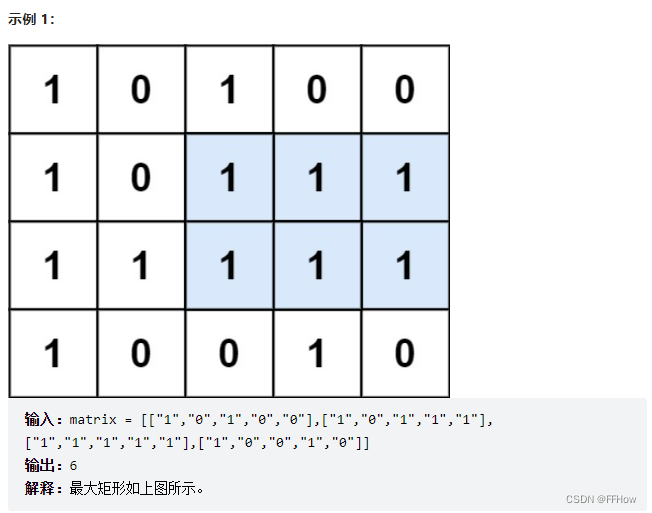
例子也非常直观，我们瞬间就明白了这是在做什么。

方法一

首先有一个较为笨的方法，就是搜索每个元素，并计算出以它为右下角的矩阵的最大面积。
这里需要用到动态规划的思想。因为为了能快速计算它为右下角的矩阵的最大面积，需要提前用一个矩阵mat_info记录下每行到它这里有多少个连续的1，即以当前元素为右顶点的水平边最大有多长。
当计算出mat_info后，我们便能依次遍历矩阵每个元素x，然后从它向上开始搜索（搜索竖边），来找出所有以x为右下顶点的矩阵，进而找出它们面积的最大值。

代码如下：

class Solution(object):
    def maximalRectangle(self, matrix):
        """
        :type matrix: List[List[str]]
        :rtype: int
        """
        count = 0       #计数有多少个连续的1
        row_num = len(matrix)
        col_num = len(matrix[0])
        mat_info = [[0 for i in range(col_num)] for j in range(row_num)]
        for row_idx, item in enumerate(matrix):
            count = 0
            for col_idx, ele in enumerate(item):
                count = 0 if ele == '0' else count + 1
                mat_info[row_idx][col_idx] = count
        # print(matrix)
        max_area = 0
        for row_idx in range(row_num):
            for col_idx in range(col_num):
                min_width = mat_info[row_idx][col_idx]
                for up in range(row_idx, -1, -1):       #从当前行往上搜索。
                    if not matrix[up][col_idx]:  #若该元素为0，则无需继续向上搜索。
                        break
                    min_width = min(min_width, mat_info[up][col_idx])
                    max_area = max(max_area, min_width * (row_idx - up + 1))
        return max_area

方法二

经点拨，发现该题目就是之前矩阵最大面积的变种。

class Solution(object):
    def maximalRectangle(self, matrix):
        max_area = 0
        row_num = len(matrix)
        col_num = len(matrix[0])
        # mat_info = [[int(matrix[j][i]) for i in range(col_num)] for j in range(row_num)]
        for j in range(col_num):
            matrix[0][j] = int(matrix[0][j])
        for i in range(1, row_num):
            for j in range(col_num):
                matrix[i][j] = 0 if matrix[i][j] == '0' else matrix[i - 1][j] + 1

        for item in matrix:
            stack = [0]
            item = [0] + item + [0]
            for i in range(1, len(item)):
                while item[i] < item[stack[-1]]:
                    ele = stack.pop()
                    new_area = (i - stack[-1] - 1) * item[ele]
                    max_area = max(max_area, new_area)
                stack.append(i)

        return max_area