【AIGC】关于LLM你必须知道的特性-偏差（bias）

代码和数据:https://github.com/tonyzhaozh/few-shot-learning

一、实践验证的大模型的特性

1. 大模型的偏差

示例：（文本的情感分析：一句话->P(积极）或者N（消极)

Input: I hate this movie. Sentiment: Negative
Input: I love this movie. Sentiment: Positive

如果不做调整，对于无意义输入，比如“N/A”或者“”Nothing，LLM回答的概率如下：

p("Positive" | "Input: N/A Sentiment:") = 0.9
p("Negative" | "Input: N/A Sentiment:") = 0.1

因为LLM的训练语料里可能更多积极的东西，所以LLM更倾向于输出P（这就是bias的来源）。期望的是P50%, N50%。

2. 大模型偏差形成的原因

大模型的bias主要有以下几种原因：

• 多数类标签偏差（样本）：大模型在预测结果时会偏向出现频率较高的答案，即偏向与prompt中出现频率较高的标签。例如，在文本分类任务中，如果一个类别的样本数量比其他类别多，模型会更倾向于预测这个多数类别，导致其他类别的准确率下降。
• 最近性偏差（样本）：大模型会倾向于重复出现在prompt末尾的答案。当prompt末尾出现多个相同的答案时，模型会更倾向于预测这个答案。这种偏差可以比多数类标签偏差更加影响预测结果。
• 常见词偏差（预训练语料）：大模型在预测结果时更倾向于输出在预训练数据中常见的词汇。这有助于解释为什么标签名称的选择很重要。

以上是导致大模型bias的主要原因，这些偏差会使得模型在few-shot学习中的准确率变化较大，但通过进行上下文校准可以减少这些偏差并提高模型的准确率。

多数类标签偏差，最近性偏差：

3. prompt的组成

prompt由三个组成部分组成：

• 格式（format）
• 一组训练样例（examples）
• 这些样例的排列顺序（permutation/ordering）

可通过改变着这三个部分，消除偏差

4. 实验和实验数据

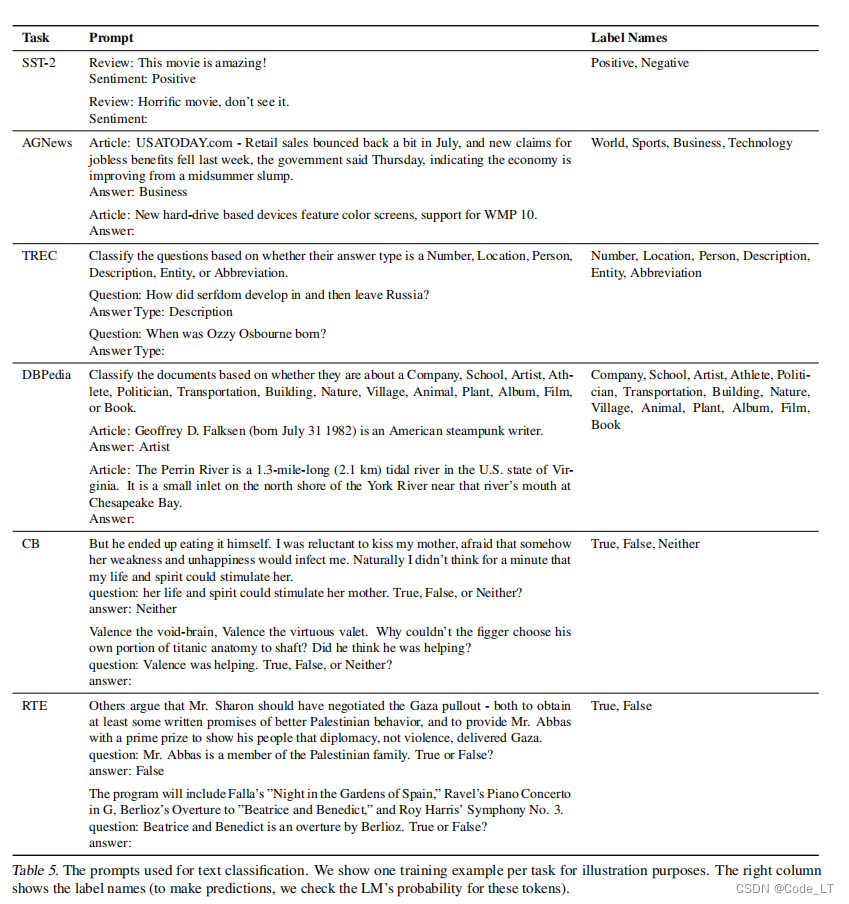
5. 现有事实

5.1 样例数和模型大小

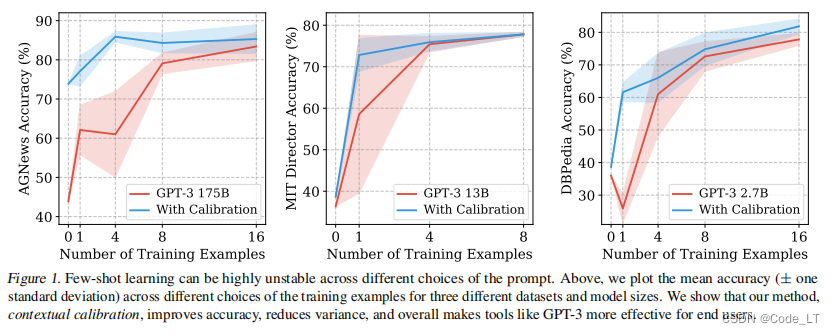
看红色区域，结论：

1. 准确性的方差不会因为于更多的数据和更大的模型而减少。一定程度后，在prompt中添加更多的训练示例并不一定会降低方差。
2. 此外，添加更多的训练示例有时会影响准确性（例如，DBPedia 0到1-shot的平均准确性从36.0%下降到25.9%）。

遗留：方差的出现是因为temperature没设置成0还是选取的样例的差异导致？

5.2 样例顺序

基础：箱线图怎么看？

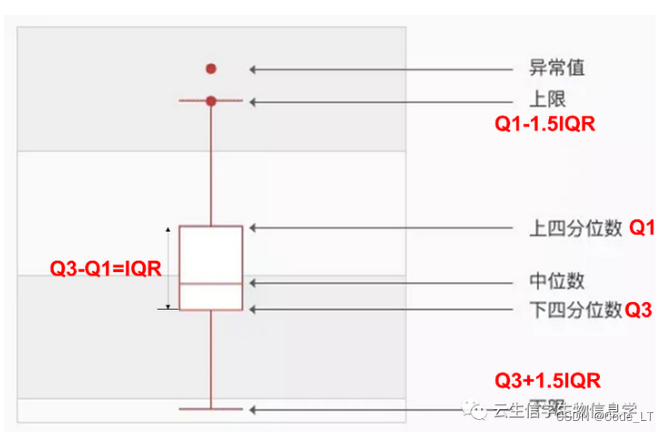
箱子大小：四分位数间距（IQR）

使用一个固定的prompt格式，只选择不同的随机训练示例集。对于每一组训练示例，评估所有可能的排列的准确性,下图为SST-2数据4-shot的结果：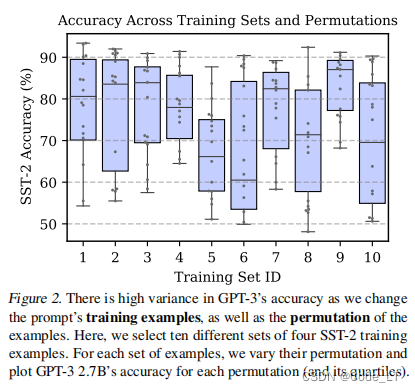
一共抽了10组数据，结论：

1. 不同样例的选择，对结果的影响也大（可能同种样例选得过多）
2. 不同的排列，对结果的影响特别大

样例顺序的例子：

5.3 prompt格式

保持训练示例和排列集的固定不变，但改变prompt格式， SST-2数据集，用下面15个format，

其中10个format的表现：

仍然时4-shot不同的训练集得到的箱线图。

结论：

1. 其中一些格式平均比其他格式好
2. 所有的格式在不同的训练集之间仍然存在很大的差异

遗留问题

1. 生成问题，不用限定最大值吗？

二、解决方案

可同时解决上面三种原因引起的偏差。

首先，LLM可以输出候选token以及其对应概率（非归一化的，openAI一次最多只能给出top的5个，但可以想办法让它给出更多，见后面章节）：

假设候选标签为A、B、C、D，则上述方法调用并归一化后可得到：
$$\hat{p}=p([\begin{array}{c}A\\ B\end{array}$$