hdu3988 Harry Potter and the Hide Story（数论-勒让德定理-质因子分解）

最新推荐文章于 2022-07-07 07:09:37 发布

小衣同学

最新推荐文章于 2022-07-07 07:09:37 发布

阅读量451

点赞数

CC 4.0 BY-SA版权

分类专栏：数论文章标签：数论质因子分解勒让德定理

本文链接：https://blog.youkuaiyun.com/Code92007/article/details/84996521

数论专栏收录该内容

45 篇文章

订阅专栏

本文介绍了一种求解k的最大次方数，该次方数能被n!整除的算法。通过预处理素数并优化循环条件，实现高效求解。分享了算法实现过程中的常见错误及解决策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

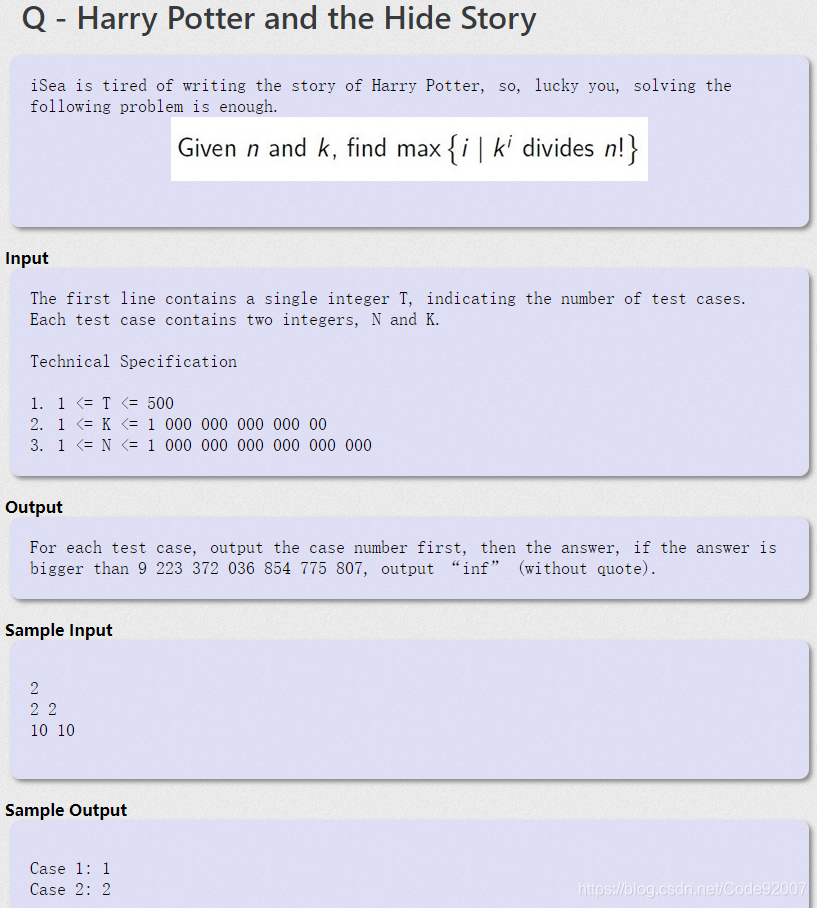
题意

给出一个n，一个k，求k的最大次方ans，能被n!整除

思路来源

http://www.cnblogs.com/toyking/p/3893157.html

题解

先预处理1e7以内的素数，O(nlognlogn)

每个k，对素数表里跑一遍，

这样素数枚举的时候，O(T·cnt)，就不是O(T·sqrt(k))了

剩下的操作，和今晚的上个题相同（见上篇UVA-10780），

就是数据量大了点。

心得

这题WA了五发，心态爆炸……

①int i*i可能爆int，埃氏筛法改了一发

②ans可能大于1e18，令n=1e18,k=2即可，但这种情况也不会超过2e18

因此将ans至少初始化为2e18，只有k=1的情况是inf

③unsigned long long，后来证明没必要，不会爆1e19

④循环i*=t的时候可能爆ll，所以改成从n向下除

⑤开始把n和k的顺序搞反了

⑥prime数组只开了1e5，后来扩容开到1e6，后来证明没必要

⑦map整数枚举的时候，prime[i]＞n了直接break跳出，能将时间从4960ms缩到1760ms

代码风格还是太辣鸡，各种出小错。

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
const int maxn=1e7+10;
const int maxm=1e5+10;
using namespace std;
typedef long long ll;
bool notprime[maxn];
ll cnt,prime[maxm];
int t;
void init()
{
	for(ll i=2;i<maxn;++i)
	{
		if(notprime[i])continue;
		prime[cnt++]=i;
		for(ll j=i*i;j<maxn;j+=i)//i*i可能爆int 
		notprime[j]=1;
	}
}
map<ll,ll>q;
map<ll,ll>fac(ll n)
{
	map<ll,ll>res;
	for(int i=0;i<cnt;++i)
	{
		if(prime[i]>n)break;
	    while(n%prime[i]==0)
		{
			++res[prime[i]];
			n/=prime[i];
		}
	}
	if(n!=1)res[n]=1;
	return res;
}
int main()
{
	init();
	scanf("%d",&t);
	for(int k=1;k<=t;++k)
	{
		ll n,m,cnt=0;
		ll ans=2e18;
		q.clear();
		scanf("%lld%lld",&n,&m);
		printf("Case %d: ",k);
		if(m==1)
		{
			puts("inf");
			continue;
		}
		q=fac(m);
		for(map<ll,ll>::iterator it=q.begin();it!=q.end();++it)
		{
			ll t=it->first,num=it->second,tmp=0;
			ll nn=n;
			while(nn>0)
			{
				tmp+=nn/t;
				nn/=t;
			}
			tmp/=num;
			ans=min(ans,tmp);
		}
	    printf("%lld\n",ans);//0也输出0 
	}
	return 0;
}