大模型论文 | 一文详解RoPE位置编码

本文详细介绍了旋转式位置编码(RoPE)的原理与优势。RoPE通过旋转矩阵将位置信息编码到Query和Key向量中，实现了相对位置的自然建模，相比传统正余弦编码具有更好的外推能力和长程衰减特性。RoPE不改变向量模长，而是通过旋转角度编码位置信息，使模型能够更好地区分位置和语义信息，成为当前大模型中更受欢迎的位置编码方法。

---

引言

Transformer的论文中提到了采用正余弦位置编码，然而，在当前各种主流大模型中，RoPE位置编码被更为广泛的使用，本文就来学习一下这种编码方式。

旋转式位置编码（Rotary Position Embedding，RoPE）由追一科技的研究团队在2021年提出。

论文标题：RoFormer: Enhanced Transformer with Rotary Position Embedding

论文地址：https://arxiv.org/pdf/2104.09864

1. 正余弦位置编码回顾
   ============

首先回顾一下 Transformer 中的正余弦位置编码。

对于序列中第 pos 个位置，位置编码向量的第 i 个维度为：

• pos = 单词在句子中的位置 (0, 1, 2, …)
• i = 维度下标 (0, 1, 2, …)
• d_model = embedding 的维度 (如 512)

下图[2]是在二维情况下，对正余弦位置编码可视化呈现，输入到模型后的向量值就是将位置编码值和向量本身进行相加。

这种绝对编码的方式会导致模型更加倾向于“记忆”位置，而不是去“推断”token的位置信息，就像图中的向量可视化之后的结果，所有的向量“无规律”地散布。

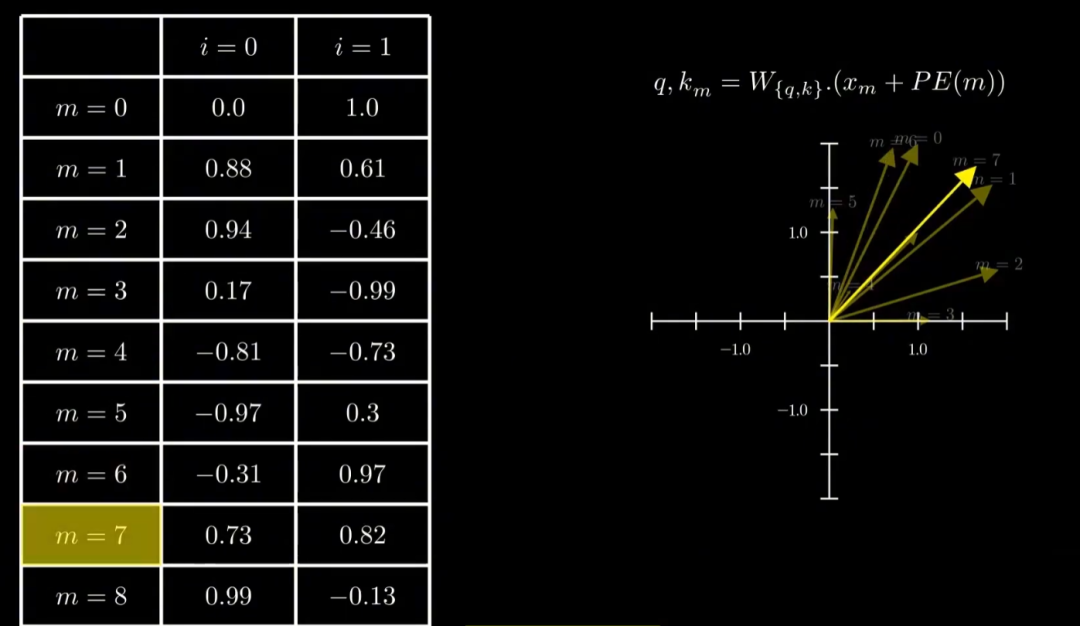
此外，这种编码方式的外推能力有限，虽然公式是连续的，理论上能生成无限长序列的编码，但在训练长度之外效果会急剧下降。

下图[2]展示了一个外推能力展现的可视化结果，随着序列长度的变长，模型的困惑度显著增加。

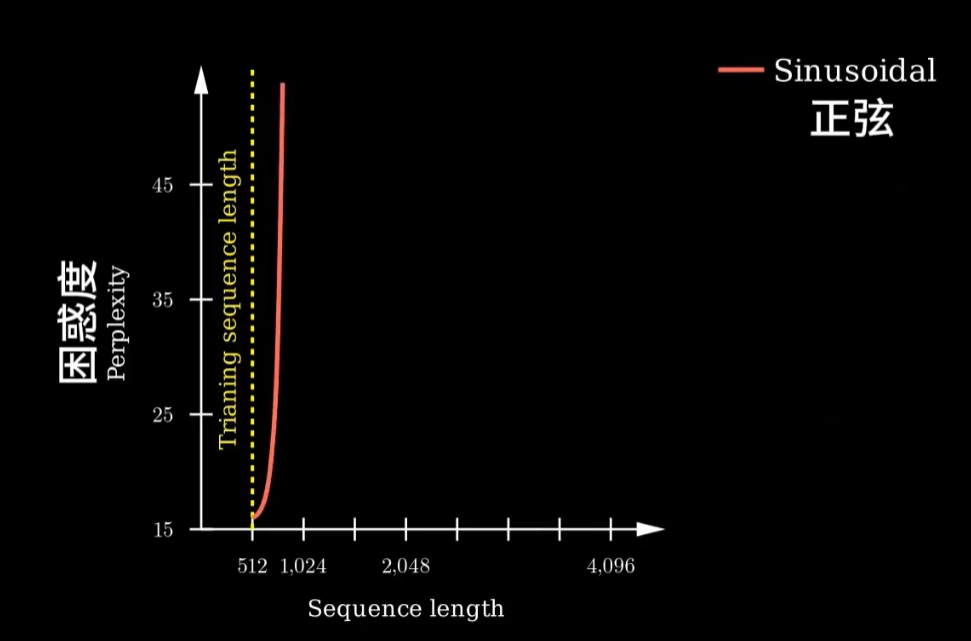
2. 绝对位置编码和相对位置编码
   ================

既然正余弦位置编码有缺陷，那是否可以通过其它编码方式进行解决。

大体上，位置编码可分成绝对位置编码和相对位置编码两大类。

2.1 绝对位置编码

绝对位置编码是最早的方案，即为序列中的每个位置 分配一个唯一的向量 ，并与 token embedding 相加：

其中， 是词向量， 是位置向量。

• 固定型：如正余弦位置编码（sin/cos），不需要训练参数。
• 可学习型：如 BERT、ALBERT，直接为每个位置设置一个可学习向量，训练时自动更新。

优点：实现简单，直接把位置信息叠加到 token 上。

缺点：

• 只能表达 绝对位置信息，无法显式捕捉 token 之间的 相对距离。
• 外推能力有限，训练时设定的最大长度就是模型的硬限制。

2.2 相对位置编码

相比绝对位置，相对位置编码更符合自然语言的需求。它直接把 位置差 融入注意力权重：

其中， 是一个依赖相对位置的可学习偏置。也可以直接把相对位置向量加入到 key 或 value 表示中，例如：

这样，注意力不仅考虑了 token 的语义，还显式建模了它们之间的相对距离。

优点：

• 能直接建模“相隔 1 个词”和“相隔 10 个词”的不同影响，更贴近语言规律。
• 泛化性更好，理论上不受训练长度的限制。

缺点：

• 实现复杂度更高，需要额外参数。
• 一些设计（如 clip 相对距离）可能损失长距离信息。
• 大多数实现仍然是 “加法式” 注入位置，不易与 线性注意力（Performer 等） 兼容。

此部分更详尽的内容可参考 RoPE 一作苏剑林大佬的博客[3]作为引申阅读，RoPE的提出是集各家所长，兼具两者的优点。

3. 旋转矩阵基础
   =========

RoPE 的核心思想是利用 旋转矩阵（Rotation Matrix） 来把位置信息编码进向量表示中。

在二维空间中，一个向量 经过旋转角度 后，会得到新的向量：

这个矩阵称为 二维旋转矩阵。

下图[4]展现了在二维情况下，(1, 0) 向量是如何通过旋转矩阵实现旋转的。

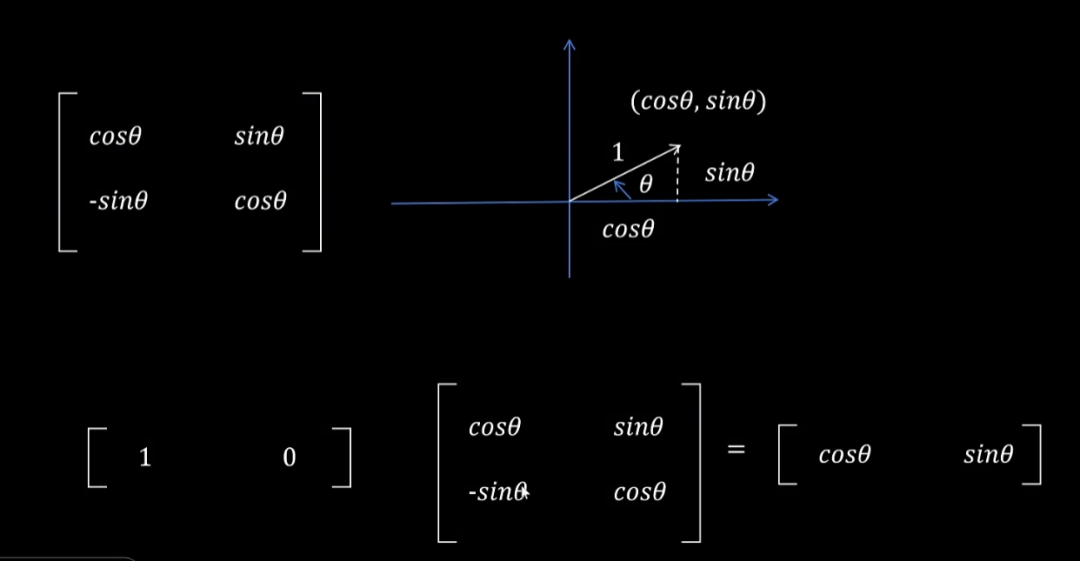
同理，如果不在第一象限，(0, 1)向量仍然可以表示成旋转角的表征形式。

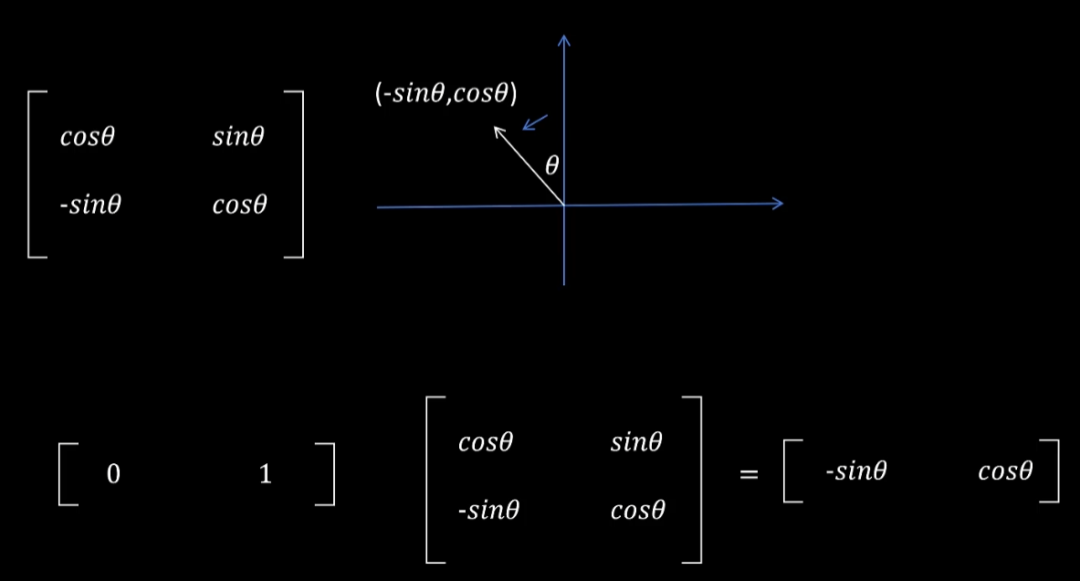
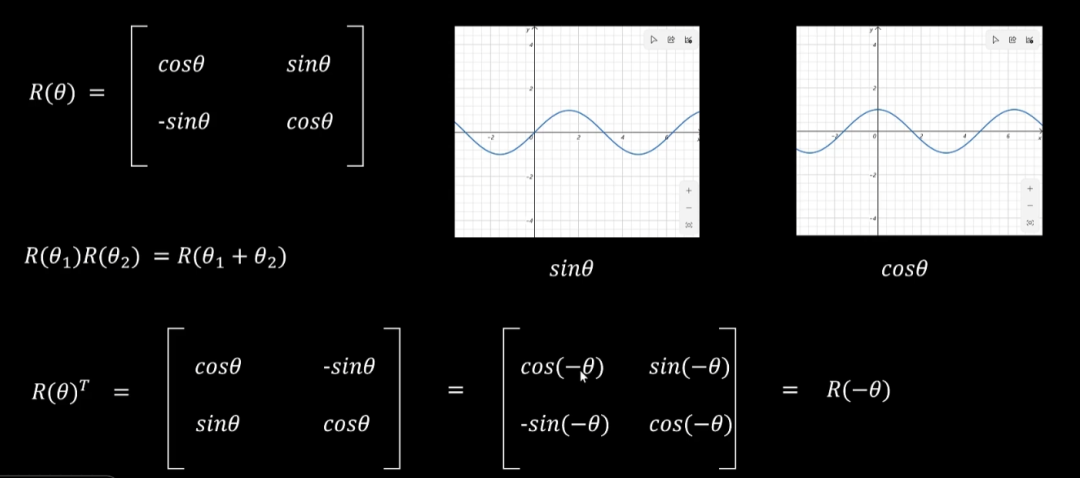
旋转矩阵具有以下基本性质：

• 1.保持模长不变

旋转只改变方向，不改变向量长度。

• 2.正交性

这保证了数值稳定性，旋转不会导致向量数值爆炸或衰减。

• 3.可叠加性

这些基本性质可以通过三角函数的基本性质推导得到，如下图[4]所示。

4. RoPE位置编码
   ===========

有了旋转矩阵的基本概念之后，就能进一步理解RoPE位置编码在做什么。

RoPE 的核心思想是：利用旋转矩阵把 token 的位置信息直接编码到 Query 和 Key 向量中，从而在注意力计算时自然体现 相对位置差。

4.1 定义

假设输入序列中第 个位置的 Query 和第 个位置的 Key 向量分别为 ，那么在 RoPE 中，它们会经过位置相关的旋转：

其中：

• 表示与位置 相关的旋转矩阵；
• 是一组频率参数；
• 每两个维度 作为一个二维平面，旋转角度为 。

4.2 注意力

传统注意力的内积为：

加入 RoPE 后：

最终结果只依赖于相对位置差 ，这意味着模型在计算注意力时，不需要显式设计额外的相对位置项，相对位置信息自然融入到旋转操作里。

原论文[1]的插图清晰地展现了这一过程。

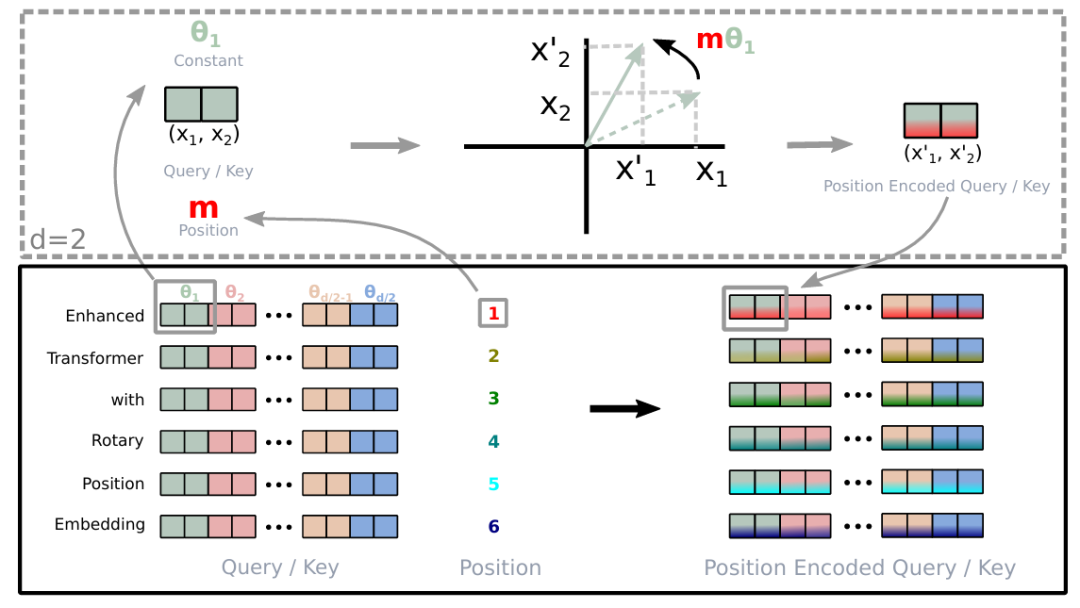
最终，算上Q,K,V，完整的注意力机制公式如下[1]：

初看会有点奇怪，因为 Transformer 原论文对注意力机制的公式中是有个 Softmax，这个去哪了？

这是有个历史原因，2020年，Katharopoulos等人的工作[5]用 核函数近似 softmax，把原来 O(N²) 的计算降到 O(Nd)，RoPE延用了这篇工作成果。

4.3 多维场景

由于旋转矩阵的维度是 2x2，为推广到多维场景，实现并行计算，RoPE 将 -维空间划分为 个二维子空间，并在每个子空间中分别应用旋转。

旋转矩阵可以表示如下：

其中频率参数集合为：

这与正余弦位置编码中的频率设计保持一致，只是由“加法”变为“旋转”。

4.4 可视化理解

和正余弦位置编码相同的方式进行可视化，如下图[2]所示，RoPE不改变向量本身的模长，而是通过旋转角让不同位置的向量进行“逆时针”旋转，这样不同位置的向量会非常清晰。

用一种更为直观的方式理解：

• 正余弦位置编码是直接相加，位置信息和向量信息黏在一块，让模型都不知道最终的向量值是位置的贡献还是向量语义的贡献。
• RoPE是巧妙把“语义”和“位置”分离，把位置信息编码进向量的相位，实现了两者的解耦，这样模型能够更好地进行学习。

这样带来的好处显而易见，如下图[2]所示，RoPE能够显著降低模型随序列长度边长而困惑度增加的趋势，外推能力更强。

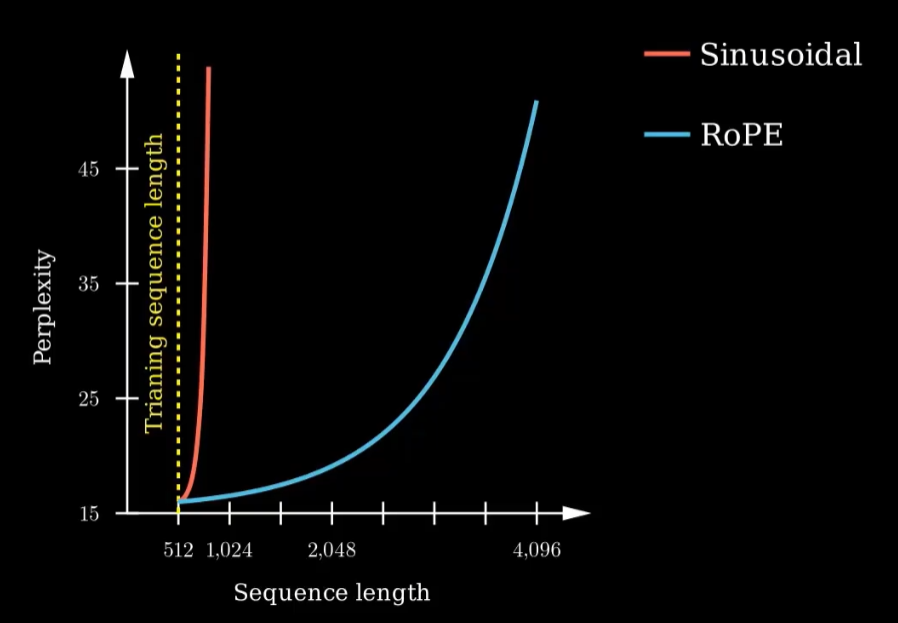
4.5 长程衰减特性

除此之外，RoPE论文[1]中还进一步介绍了RoPE具有长程衰减的特性。

在 RoPE 中，Query 和 Key 的相似度受到相对位置差 的影响。 当 较大时：

• 每个维度对 会被旋转 ；
• 高频维度（ 较大）旋转更快，导致内积振荡甚至抵消；
• 多个频率叠加后，整体效果就是 随着距离增大，内积逐渐减小。

这意味着 RoPE 天然具有 长程衰减性：token 距离越远，相关性越弱，更符合自然语言规律，也是 RoPE 的一大优势，可视化效果如下图[1]所示，

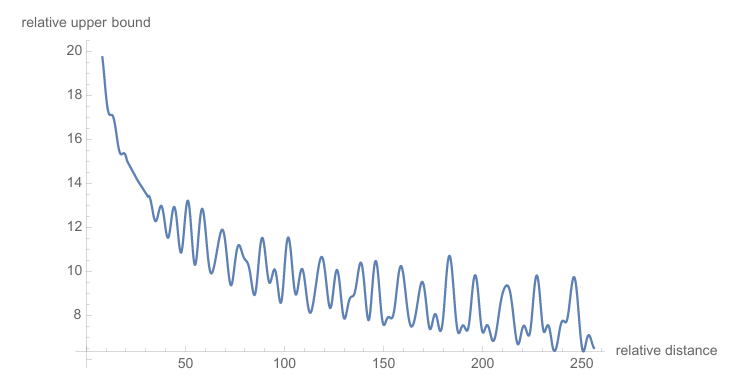
总结

RoPE 通过旋转相位的方式优雅地将位置信息嵌入 Transformer 中，不仅弥补了正余弦编码的不足，还实现了相对位置建模、长程衰减、外推能力的多重优势，因此成为大模型中更为广泛使用的位置编码方法。

---

如何系统学习掌握AI大模型？

AI大模型作为人工智能领域的重要技术突破，正成为推动各行各业创新和转型的关键力量。抓住AI大模型的风口，掌握AI大模型的知识和技能将变得越来越重要。

学习AI大模型是一个系统的过程，需要从基础开始，逐步深入到更高级的技术。

这里给大家精心整理了一份全面的AI大模型学习资源，包括：AI大模型全套学习路线图（从入门到实战）、精品AI大模型学习书籍手册、视频教程、实战学习、面试题等，资料免费分享！

1. 成长路线图&学习规划

要学习一门新的技术，作为新手一定要先学习成长路线图，方向不对，努力白费。

这里，我们为新手和想要进一步提升的专业人士准备了一份详细的学习成长路线图和规划。可以说是最科学最系统的学习成长路线。

2. 大模型经典PDF书籍

书籍和学习文档资料是学习大模型过程中必不可少的，我们精选了一系列深入探讨大模型技术的书籍和学习文档，它们由领域内的顶尖专家撰写，内容全面、深入、详尽，为你学习大模型提供坚实的理论基础。（书籍含电子版PDF）

3. 大模型视频教程

对于很多自学或者没有基础的同学来说，书籍这些纯文字类的学习教材会觉得比较晦涩难以理解，因此，我们提供了丰富的大模型视频教程，以动态、形象的方式展示技术概念，帮助你更快、更轻松地掌握核心知识。

4. 大模型行业报告

行业分析主要包括对不同行业的现状、趋势、问题、机会等进行系统地调研和评估，以了解哪些行业更适合引入大模型的技术和应用，以及在哪些方面可以发挥大模型的优势。

5. 大模型项目实战

学以致用 ，当你的理论知识积累到一定程度，就需要通过项目实战，在实际操作中检验和巩固你所学到的知识，同时为你找工作和职业发展打下坚实的基础。

6. 大模型面试题

面试不仅是技术的较量，更需要充分的准备。

在你已经掌握了大模型技术之后，就需要开始准备面试，我们将提供精心整理的大模型面试题库，涵盖当前面试中可能遇到的各种技术问题，让你在面试中游刃有余。

全套的AI大模型学习资源已经整理打包，有需要的小伙伴可以微信扫描下方优快云官方认证二维码，免费领取【保证100%免费】

参考

[1] RoFormer: Enhanced Transformer with Rotary Position Embedding: https://arxiv.org/pdf/2104.09864

[2] 终于知道Transformer 为啥离不开 RoPE了：https://www.bilibili.com/video/BV166egzvE9H

[3] 让研究人员绞尽脑汁的Transformer位置编码：https://kexue.fm/archives/8130

[4] 你还不懂旋转位置编码吗？：https://www.bilibili.com/video/BV1F1421B7iv

[5] Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention:https://arxiv.org/abs/2006.16236