本文作为一篇学习笔记,在图片和文字上大量参考了各种密码学书籍,并添加了自己的注解和理解;古典密码学的学习需要一些数论的知识,比如模运算、扩展的欧几里得算法;在入门学习过程中没必要系统地学习数论,只需学习必要知识即可
古典密码的加密思想和方法在现代密码学中仍然在使用,古典密码的加密技术主要分为
- 替代技术
- 置换技术
参考资料
《网络安全理论与应用》余研 付安民 …编著
《图解密码技术》第三版 结成浩著
替代技术
替代技术是将明文中的每个元素映射为另一个元素的技术。若把明文视为二进制序列,则替代技术就是用密文序列来代替明文序列。代替后,字母位置不变,其本身的值发生改变。而后面介绍的置换技术是字母的值不变,字母在明文中的位置发生改变。
注解:
DES的S盒就是一张替代表
元素指的是:字母、比特、比特组合或字母组合
根据替代是对每个字母逐个进行还是对多个字母同时进行,古典密码又可以分为
- 单字母表替代密码
- 多字母表替代密码
基于替代技术的古典密码有凯撒密码、移位密码、仿射密码、Vigenere密码、Hill密码等。
单字母表替代密码
凯撒密码
凯撒密码是已知最早的替代密码。凯撒密码将字母表视为一个循环的表,将明文中的每个字母使用字母表中其后的第三个字母来代替;
凯撒密码中明文字母和密文字母的对应关系

例如
若明文为i will go fishing tomorrow
则密文为L ZLOO JLVKLQJ WRPRUURZ
若令每个字母对应一个数字(a=0, b=1, …, z=25),m表示明文字母,c表示密文字母,且0≤m,c≤25,则凯撒算法的加密和解密可以形式化表示为
c
=
E
3
(
m
)
=
(
m
+
3
)
m
o
d
26
c=E_3 (m)=(m+3) mod 26
c=E3(m)=(m+3)mod26
m
=
D
3
(
c
)
=
(
c
−
3
)
m
o
d
26
m=D_3 (c)=(c-3) mod 26
m=D3(c)=(c−3)mod26
可见,3是加解密所使用的密钥。
在凯撒密码中,密钥的值固定为3,因此很容易对凯撒密码进行攻击。
移位密码
为了增大凯撒密码的密钥空间,将凯撒密码的加解密算法进行一般化,定义密文字母和明文字母的偏移可以是任意值,即定义移位密码的加密和解密形式为
c
=
E
k
(
m
)
=
(
m
+
k
)
m
o
d
26
c=E_k (m)=(m+k) mod 26
c=Ek(m)=(m+k)mod26
m
=
D
k
(
c
)
=
(
c
−
k
)
m
o
d
26
m=D_k (c)=(c-k) mod 26
m=Dk(c)=(c−k)mod26
其中,0≤m,c≤25,k为算法的密钥,且0≤k≤25。
尽管移位算法将密钥空间扩展至字母表的长度,但其密钥空间仍然太小,只有26种可能的取值,仍然可以轻易地穷举整个密钥空间来破译密文,平均只需尝试26/2=13次即可计算得到明文。
仿射密码
移位密码的密钥空间太小,仿射密码就是移位密码的更一般形式;在仿射密码中,加密函数定义为
c
=
E
(
a
,
b
)
(
m
)
=
(
a
m
+
b
)
m
o
d
26
c=E_{(a,b)} (m)=(am+b) mod 26
c=E(a,b)(m)=(am+b)mod26 (1)
其中
a
,
b
∈
Z
26
a,b∈Z_{26}
a,b∈Z26。形如上式的函数被称为仿射函数,因此该密码体制也被称为仿射密码。
特别地,当a = 1时,移位密码为仿射密码的特殊形式。
为了能对密文进行解密,必须保证所使用的仿射函数是一个单射函数,即对于任意的 c ∈ Z 26 c∈Z_{26} c∈Z26,同余方程 a m ≡ ( c − b ) m o d 26 am≡(c-b) mod 26 am≡(c−b)mod26 有惟一解m
可以证明,当 g c d ( a , 26 ) = 1 gcd(a,26)=1 gcd(a,26)=1时, a a a在 Z 26 Z_{26} Z26上存在乘法逆元 a − 1 a^{-1} a−1,使得同余方程存在惟一解: m = a − 1 ( c − b ) m o d 26 m=a^{-1} (c-b) mod 26 m=a−1(c−b)mod26 (2)
(2)式由同余的除法得到
gcd是greatest common digital, 其中gcd(c,m)表示c和m的最大公约数
因此,仿射密码的解密函数可以定义为
m
=
D
(
a
,
b
)
(
c
)
=
a
−
1
(
c
−
b
)
m
o
d
26
m=D_{(a,b)} (c)=a^{-1} (c-b) mod 26
m=D(a,b)(c)=a−1(c−b)mod26
其中,a,b是密钥,且为满足
(
a
,
b
)
∈
Z
26
×
Z
26
(a,b)∈Z_{26}×Z_{26}
(a,b)∈Z26×Z26和
g
c
d
(
a
,
26
)
=
1
gcd(a,26)=1
gcd(a,26)=1的整数。
案例
加密:

解密:

加密很容易计算,这里不在叙述;
解密使用扩展的欧几里得算法:步骤如下
- 用扩展的欧几里得算法求的乘法逆元a-1
- 乘法逆元算出来后,进行模运算即可
求乘法逆元手算如下
因为
7
x
=
1
m
o
d
26
7x = 1mod 26
7x=1mod26, x的取值即为7mod26下的乘法逆元
7
x
+
26
y
=
g
c
d
(
7
,
26
)
=
1
7x + 26y = gcd(7,26)=1
7x+26y=gcd(7,26)=1 记为 (2)
用扩展的欧几里得算法求出x即可
运算过程如下:
第一步:进行辗转相除(写成等式形式)
26 = 3×7 + 5; ⇒ 5 = 26 - 3×7
7 = 1×5 + 2; ⇒ 2 = 7 -1×5
5 = 2×2 + 1; 1 = 5 - 2×2
其中 26为被除数,3为商,7为除数,5为余数;将余数5用26和7表示出来,方便后面进行回带
回带过程
为了求出x,根据(2)式用7和26表示1即可算出x和y的值;可以通过保持商不变,替换掉除1以外的所有余数来实现;
1 = 26 - 3×7 - 2×[ 7 - 1×(26 - 3×7 ) ] 这里替换掉上面式子中的余数2和余数5;
1 = 3×26 - 11×7 可得到 x=-11 y=3
x = -11 mod 26 等价于 x = (-11 + 1×26) mod 26 等价于x = 15 mod 26
为了方便计算,这里取x=15即可
因此在计算时,7mod26下的乘法逆元为15;
解密函数为
m
=
D
7
,
3
(
c
)
=
15
(
c
−
3
)
m
o
d
26
m = D_{7,3} (c) = 15(c - 3) mod 26
m=D7,3(c)=15(c−3)mod26
计算举例
当c=4时,m=15(4- 3)mod 26 = 15
针对单字母表替代密码的攻击
单字母表替代密码可以实现字母表中26个字母的任意替代,密钥空间大小为26!,即有大于 4 × 1 0 26 4×10^{26} 4×1026种可能的密钥,即使每微秒尝试一个密钥,也需要花费约 1 0 13 10^{13} 1013年才能穷举所有的密钥。因此,单字母表替代密码可以抵御强行攻击。
然而,如果密码攻击者知道明文的性质(例如,明文是自然语言文本),则攻击者可以利用该自然语言的某些统计特性实施攻击。
例如,在英语中,字母出现频率依次为e(12.75%),其次分别为t(9.25%)、r(8.5%)、i(7.75%)、n(7.75%)以及o(7.5%)等,字母的出现频率呈现出一定的统计特性。
攻击者可以根据密文中字母、双字母组合(如th)甚至三字母组合(如the)出现的相对频率进行猜测,只要密文足够长,攻击者即可由明文推导出密文
攻击者利用明文的统计特性针对单字母替代密码实施攻击的步骤如下:
- 攻击者确定密文中字母出现的相对频率;
- 将密文字母的出现频率与自然语言的标准频率分布进行比较;
- 还可以观察双字母组合和三字母组合等,以便对明文进行猜测。
频率分析的具体案例可以参考《图解密码技术》
局限性:由于单字母替代密码反映了原来字母表的频率特性,因此很容易被攻破;
多字母表替代密码
为了减少密文中明文结构的残余度,改善单字母密码的强度,出现了多字母密码技术。
在多字母替代密码中,处理明文消息时使用了不同的单字母替代。
多字母替代密码通常具有以下性质:
- 使用一系列相关的单字母替代规则;
- 由密钥决定对于一个给定的变换选择哪种特定的规则。
典型的多字母表替代密码包括Vigenère密码、Hill密码等。
Vigenere密码
多字母表替代密码中最著名和最简单的密码是Vigenère密码,其发明者是16世纪的法国人Blaise de Vigenère。
Vigenère密码的替代表由26个移位密码替代表组成,它在处理明文消息中的每个字母时使用了不同的单字母替代。
加密过程可以形式化描述为 c i = ( m i + k i m o d r ) m o d 26 c_i=(m_i+k_{i mod {r}}) mod 26 ci=(mi+kimodr)mod26
因此,Vigenère密码本质上是对每个明文字母使用了不同的单字母替代密码,而具体使用哪个单字母替代表则是由密钥字母确定。

其解密过程如下:
m
i
=
(
c
i
−
k
i
m
o
d
r
)
m
o
d
26
m_i=(c_i-k_{i mod r}) mod 26
mi=(ci−kimodr)mod26
Vigenère密码的加解密过程中,重复使用相同的密钥字母串K,直至所有的消息均加解密完成。
案例
例:假设密钥字为“HAPPYTIME”,待加密的明文为“please send the data”,试计算相应的密文。
解:密钥对应的数字串为K=(7,0,15,15,24,19,8,12,4),将密钥串重复书写在由明文串转换的数字上方,进行模26下的加密运算,如下所示:

对应的密文串为WLTPQXAQRKTWTBTBM。
解密时使用相同的密钥字进行逆运算即可。
总结
Vigenère密码中不同的密钥对应着不同的单字母替代,其密钥空间的大小为
2
6
r
26^r
26r,即使r值很小,使用穷尽搜索方法也需要很长的时间才能遍历密钥空间,因此,多字母表替代密码的安全性要比单字母表替代密码的安全性要好
Hill密码(希尔密码)
Hill密码是一种具有代表性的多字母表替代密码,由Lester S. Hill于1929年提出。
Hill密码使用了线性变换来实现加密解密功能。
加密过程
在Hill密码中,首先将明文M划分为由n个字母构成的分组
M
=
(
m
1
,
m
2
,
.
.
.
,
m
n
)
M=(m_1,m_2,...,m_n)
M=(m1,m2,...,mn),密钥K取为n×n的矩阵,对于明文M和密钥K,计算密文C如下:
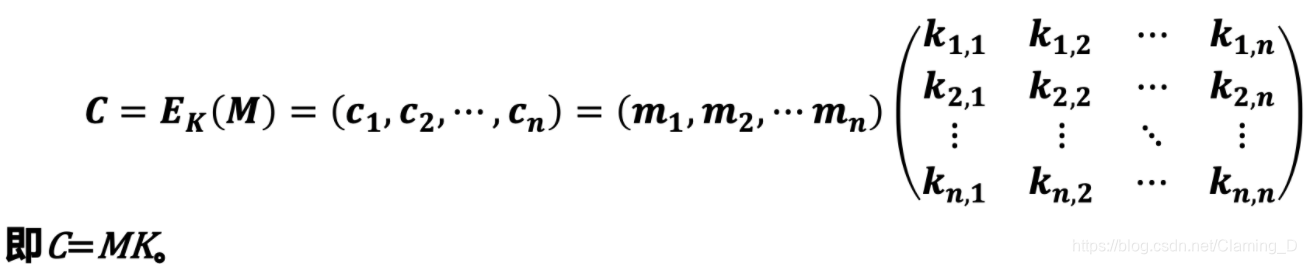
解密过程
在Hill密码中密文是通过明文进行线性变换得到。若要从密文中计算得到明文,需要进行解密变换,相应的明文应为
M
=
C
K
−
1
M=CK^{-1}
M=CK−1。即要求矩阵
K
K
K在模
q
q
q的情形下存在可逆矩阵
K
−
1
K^{-1}
K−1。
由线性代数可知,矩阵K在模q的情形下存在可逆矩阵K-1的充分必要条件是
g
c
d
(
∣
K
∣
,
q
)
=
1
gcd(|K|, q)=1
gcd(∣K∣,q)=1,且
K
−
1
=
∣
K
∣
−
1
K
∗
K-1=|K|-1K^{*}
K−1=∣K∣−1K∗。
因此,Hill密码的解密过程为
M
=
C
K
−
1
m
o
d
q
M=CK^{-1} mod q
M=CK−1modq
置换技术
对于基于替代技术的密码而言,其明文字母被不同的密文字母所代替。而置换密码则不同,置换技术是在不丢失信息的前提下对明文中的元素进行位置上的重新排列,以打乱明文字母的位置和顺序。
在对称密码中,经常使用各种置换表进行置换选择。
定义在有限集X上的一个置换是一个双射函数
f
:
X
→
X
f:X→X
f:X→X。即对于任意的
y
∈
X
y∈X
y∈X,存在唯一的
x
∈
X
x∈X
x∈X使得
f
(
x
)
=
y
f(x)=y
f(x)=y,从而可以定义置换f的逆置换:
f
−
1
:
X
→
X
f^{-1}:X→X
f−1:X→X
f
−
1
(
y
)
=
x
f^{-1} (y)=x
f−1(y)=x当且仅当
f
(
x
)
=
y
f(x)=y
f(x)=y
其中,
f
−
1
f^{-1}
f−1也是X上的一个置换。
置换密码的定义
假设M为明文,C为密文,令n是一正整数
,
x
i
,
y
i
∈
Z
26
,x_i,y_i∈Z_{26}
,xi,yi∈Z26,K是由所有定义在集合{1,2,…,n}上的置换组成,对于任意的置换(即密钥)f,加密过程为
C
=
E
f
(
x
1
,
x
2
,
⋯
,
x
n
)
=
(
x
f
(
1
)
,
x
f
(
2
)
,
⋯
,
x
f
(
n
)
)
C=E_f(x_1,x_2,⋯,x_n )=(x_{f(1)} ,x_{f(2)} ,⋯,x_{f(n)} )
C=Ef(x1,x2,⋯,xn)=(xf(1),xf(2),⋯,xf(n))
解密过程为
M
=
D
f
(
y
1
,
y
2
,
⋯
,
y
n
)
=
(
x
f
−
1
(
1
)
,
x
f
−
1
(
2
)
,
⋯
,
x
f
−
1
(
n
)
)
M=D_f(y_1,y_2,⋯,y_n )=(x_{f^{-1} (1) },x_{f^{-1} (2) },⋯,x_{f^{-1} (n) })
M=Df(y1,y2,⋯,yn)=(xf−1(1),xf−1(2),⋯,xf−1(n))
其中,
f
−
1
f^{-1}
f−1是置换
f
f
f的逆置换。
案例
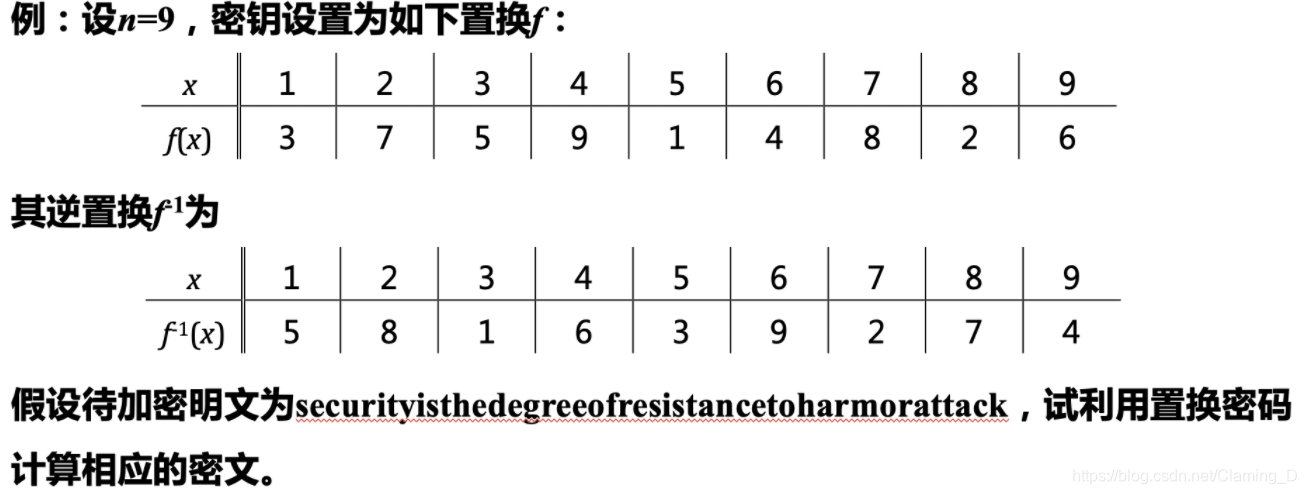
解:首先将明文分组,每9个一组:
securityi|sthedegre|eofresist|ancetohar|morattack
对每组的9个字母使用加密变换f,可得密文:
CTRISUYEI|HGDESERTE|FIETERSOS|CHTRAEANO|RATKMACOT
解密过程使用逆置换
f
−
1
f^{-1}
f−1,可恢复明文
securityi|sthedegre|eofresist|ancetohar|morattack
 古典密码学:替代与置换技术详解
古典密码学:替代与置换技术详解




















 1017
1017

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








