#leetcode#Unique Binary Trees

最新推荐文章于 2019-06-19 19:49:50 发布

原创最新推荐文章于 2019-06-19 19:49:50 发布 · 525 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode

LeetCode 专栏收录该内容

92 篇文章

订阅专栏

本文详细解析了如何通过动态规划算法计算不同数量节点的唯一二叉搜索树的数量，并提供了具体的Java实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

水中的鱼大神博客有公式的推导过程：

http://fisherlei.blogspot.com/2013/03/leetcode-unique-binary-search-trees.html

补充一下自己的理解：

再看一遍三个元素的数组，可以发现BST的取值方式如下：
Count[3] = Count[0]*Count[2] (1为根的情况) ----------- 左边无子树数乘以右边有两个节点构成的子树数目
+ Count[1]*Count[1] (2为根的情况) ----------- 左边有一个节点构成的子树数目 * 右边有一个节点构成的子树数目
+ Count[2]*Count[0] (3为根的情况) ----------- 左边由两个节点构成的子树数目乘以右边有零个节点构成的子树数目

<span style="color:#333333;">public class Solution {
    public int numTrees(int n) {
        if(n < 0 ){
            return 0;
        }
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; i++){
            for(int j = 0; j <= i - 1; j++){
                dp[i] += dp[j] * dp[i - j - 1];
            }
        }
        
        return dp[n];
    }
}</span>

递推公式为

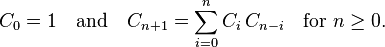
后面公式里用 n 替换 n - 1， dp对应的各个数值就是 n 的值为 0 ~ n 时对应的解的数目，也就是code中的外层循环， dp[0] == dp[1] == 1是初始条件，所以外层循环从 i = 2 开始

内层循环对应公式中的 i = 0 ~ n - 1，所以code中是从 j = 0 到 j = i - 1, 然后递推公式是

<span style="color:#333333;">dp[i] += dp[j] * dp[i - j - 1];</span>

<span style="color:#333333;">
</span>

<span style="color:#333333;">
</span>

复杂度分析：

借用code ganker大神的分析

时间上每次求解i个结点的二叉查找树数量的需要一个i步的循环，总体要求n次，所以总时间复杂度是O(1+2+...+n)=O(n^2)。空间上需要一个数组来维护，并且需要前i个的所有信息，所以是O(n)。