论文笔记 | Self-attention Enhanced Auto-encoder for LinkWeight Prediction with Graph Compression

本文链接：https://blog.youkuaiyun.com/ChA0s007/article/details/132114208

本文提出了一种结合自注意力机制的深度图学习模型SEA，用于加权图的连接权重预测。通过图压缩技术，有效处理大型图的效率问题，实验证明SEA在多个网络上优于现有方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章信息

来源：IEEE Transactions on Network Science and Engineering(TNSE 2023)

作者：Zhen Liu, Wenbo Zuo, Dongning Zhang and Chuan Zhou

链接：Self-attention Enhanced Auto-encoder for Link Weight Prediction with Graph Compression | IEEE Journals & Magazine | IEEE Xplore

代码: GitHub - wave-zuo/SEA: Self-attention Enhanced Auto-encoder for Link Weight Prediction with Graph Compression

内容简介

在各种网络系统中，与连接相关联的权重通常代表实体之间联系的强度。例如，在社交网络中，连接权重可以表示朋友之间的亲密程度；在蛋白质相互作用（PPI）网络中，连接权重可以表示蛋白质之间的相互作用频率；在航空网络中，连接权重可以表示城市之间的路线受欢迎程度。因此，除了它们作为真实网络的固有属性外，人们还认为连接权重是推动连接形成、社群增长和网络演化的关键因素之一。然而，在某些情况下，网络中的连接权重可能是缺失或未知的。例如，在PPI网络中，某些蛋白质之间的相互作用频率可能很难直接测量，只能通过预测模型来估计。因此，开发连接权重预测模型以实现加权图的完整性具有理论意义和实际关注。

与传统的图分类任务（如节点分类或连接预测）不同，对于纯加权图的连接权重预测是一个回归任务，更具挑战性且探索较少。传统上，一些研究尝试用简单的方法来解决这个问题，例如使用浅层拓扑特征来预测缺失的连接权重。例如，WCN、WAA和WRA等方法简单地利用局部图结构的底层统计特征来估计连接权重。然而，实际上，连接权重可能代表非常复杂的相互作用，如图1所示的大脑网络中神经元之间的联系强度，这些复杂的相互作用很难被浅层特征方法捕捉到。文献中也指出，网络中不均匀的权重分布可能对传统的浅层特征方法产生进一步挑战，如欠拟合问题。

因此，本工作的第一个动机是利用深层图形特征更好地表示连接权重。受到图表示学习、图神经网络（GNNs）和图嵌入（GE）方法的进展启发，这些深层图学习技术可以更准确地提取与任务相关的潜在图表示特征。同时，使用GNN或GE方法时需要谨慎处理一些潜在的风险，例如GCN中的过度平滑问题。

另一方面，必须指出，与节点分类相比，连接权重预测需要使用更多的图信息，因为给定图中连接的数量通常远远多于节点数量。当图变得非常大时，从图中提取连接特征可能成为一项繁重的任务。因此，本文的第二个动机是想知道是否可能将图压缩为较小的图，以提高图学习的效率，这也是一个较少探索的领域。

本文主要贡献：

1. 通过自注意机制聚合一阶加权邻居信息和二阶图拓扑信息，以表示连接的嵌入向量。

2. 提出了一种基于自监督学习的GNNs框架来执行加权图重构，该框架能够在缺失连接权重预测方面实现最先进的性能。

3. 提出了一种图压缩方法，可显著减小加权图的大小，同时大部分保留连接信息。实验结果表明，与未压缩情况相比，在压缩图上进行连接权重预测的准确性仍然具有竞争力。

模型框架：

A. 问题定义

给定的网络可以被形式化为一个由三元组（V，E，W）表示的加权图 $\mathcal{G}$ ，其中V是节点集合，E表示边的集合，W对应于边的权重集合。值得注意的是，在我们的问题设置中，既没有节点属性也没有节点标签，即 $\mathcal{G}$ 是一个纯加权图。如果有一组缺失或不可观察的连接权重W∗ ⊆ W，这些权重与边E∗ ⊆ E相关联，连接权重预测的目标是基于观察到的网络 $\mathcal{G}^{o}=\left(\mathcal{V}, \mathcal{E}, \mathcal{W}-\mathcal{W}^{*}\right)$ 尽可能准确地恢复缺失的权重W∗。通常，一个邻接矩阵 $A \in\{0,1\}^{|\mathcal{V}| \times|\mathcal{V}|}$ 和一个加权邻接矩阵 $W \in \mathbb{R}^{{+},|\mathcal{V}| \times|\mathcal{V}|}$ 被用来共同表示观察到的网络，在W中， $w_{u,v}=0$ 的条目表示节点u和v之间边的权重，0表示它们没有连接或连接但权重缺失。在这项工作中，仅考虑无向图，有 $w_{u,v}$ 等于 $w_{v,u}$ 。考虑到大多数现实世界的网络不包含节点之间的自连接，我们假设对角线上的元素值为零，即 $\forall u \in \mathcal{V}, a_{u, u}=0, w_{u,u}=0$ 。需要注意的是，为了避免权重值的广泛范围干扰评估指标的尺度，需要对连接权重进行预处理。需要通过以下计算将每个连接权重的值进行归一化。

$w_{\text {new }}=e^{-\frac{1}{w_{\text {old }}}} .$

因此，转换后的权重值仅限于(0, 1)范围内。在本文中，连接权重预测的任务被定义为加权图重构问题。

则对于加权图重构问题可以有以下定义。给定一个由加权邻接矩阵W和邻接矩阵A表示的观察到的加权图 $\mathcal{G}^{o}$ ，理想情况下，重构后的加权邻接矩阵W'满足以下条件：

$w_{u, v}^{\prime}=\left\{\begin{array}{cl} w_{u, v} & \text { if } w_{u, v} \neq 0 \text { and } a_{u, v}=1 \\ 0 & \text { if } w_{u, v}=0 \text { and } a_{u, v}=0 \\ w_{u, v}^{*} & \text { if } w_{u, v}=0 \text { and } a_{u, v}=1 \end{array}\right.$

其中， $w_{u, v}^{*} \in \mathcal{W}^{*}$ 对应于连接(u, v)上的缺失连接权重。

B. SEA基本框架

为了实现加权图重构，设计了一个链接级自编码器框架，包括边编码器和回归解码器两个组件，与传统的节点级表示学习方法不同。给定一条连接（u，v），链接编码器函数F(·)被用来将该连接表示为一个低维嵌入向量 $B_{u,v}$ ，表达方式如下：

$B_{u, v}={F}(W, A)$

然后，连接解码器函数G(·)将嵌入向量映射到连接(u, v)的权重。

$w_{u, v}^{\prime}={G}\left(B_{u, v}\right) .$

为了捕捉非线性的深层图形特征，考虑了节点的一阶邻居信息和二阶结构信息，用于编码初始节点表示向量，表示方式如下

$h_{u}=\left(W x_{u}\right) \|\left(A^{2} x_{u}\right),$

其中，xu是来自|V|×|V|的二进制对角矩阵的节点u的one-hot列向量，∥表示连接操作，而 $A^{2} \in \mathbb{N}^{+,|\mathcal{V}| \times|\mathcal{V}|}$ 表示二阶邻接矩阵，是通过邻接矩阵A的平方得到的。 $A^2$ 作为图的二阶拓扑信息，其中每个条目也表示相应节点对的共同邻居数量。

传统上，GAE使用GCN来聚合邻居信息以生成节点嵌入向量。经过实证研究，Graph Attention Network（GAT）被确认为在处理像连接权重预测这样的回归任务时更强大的工具。给定节点u的一阶邻居k，计算注意力系数 $a_{u,k}$ ，表示节点k对节点u的注意力程度，计算公式为：

$\begin{array}{r} \alpha_{u, k}=\frac{\exp \left(\operatorname{LeakyReLU}\left(\gamma^{T} \rho_{u, k}\right)\right)}{\sum_{j \in N_{u}} \exp \left(\operatorname{LeakyReLU}\left(\gamma^{T} \rho_{u, j}\right)\right)},\gamma \in \mathbb{R}^{|\mathcal{V}| \times 1} \end{array}$

其中

$\rho_{u, k}=\left(\Omega_{1} h_{u}\right) \oplus\left(\Omega_{2} h_{k}\right), \Omega_{1}, \Omega_{2} \in \mathbb{R}^{|\mathcal{V}| \times 2|\mathcal{V}|}$

⊕表示向量加法， $N_u$ 表示节点u的邻居集合，LeakyReLU(·)是带有负输入斜率= 0.2的Leaky修正线性单元。同样，可以通过相同的方式获得节点v的注意力系数。根据与节点u和v相关联的学习到的注意力系数，可以生成连接(u, v)的聚合嵌入向量，表示为：

$\begin{array}{r} B_{u, v}=\text { LeakyReLU }\left(\sum_{k \in N_{u}} \alpha_{u, k} \Omega_{3} h_{k} \| \sum_{j \in N_{v}} \alpha_{v, j} \Omega_{3} h_{j}\right) \Omega_{3} \in \mathbb{R}^{m \times 2|\mathcal{V}|} \end{array}$

为了获得连接上的预测权重，我们可以进行如下计算：

$w_{u, v}^{\prime}=\sigma\left(\Theta_{u, v}^{T} B_{u, v}\right)$

其中， $\Theta_{u, v} \in \mathbb{R}^{2 m \times 1}$ 是一个参数列向量，σ(·)是Sigmoid函数。上述方程对应于连接解码器函数。

C. 损失函数设置

为了得到优化的连接嵌入并最小化加权图重构误差，定义损失函数如下：

$\mathcal{L}=\sum_{u \neq v} a_{u, v}\left(w_{u, v}^{\prime}-w_{u, v}\right)^{2}+\nu \sum_{u \neq v} a_{u, v}\left\|B_{u, v}-B_{v, u}\right\|_{2}^{2}+\mathcal{L}_{\text {reg }}$

其中，如果观察到的网络中的节点u和v通过已知权重 $w_{u,v}$ 相连接，则 $a_{u,v}=1$ ，否则 $a_{u,v}=0$ 。方程中的第二项是Laplacian Eigenmaps。如果原始图中的节点u和v有连接，那么相应的连接嵌入向量 $B_{u,v}$ 和 $B_{v,u}$ 在嵌入空间中也会相互靠近。同时，正则化项用于防止过拟合，表示为

$\mathcal{L}_{\text {reg }}=\sum_{k=1}^{2} \frac{\lambda_{k}}{2}\left\|\Omega_{k}\right\|_{2}^{2}+\frac{\delta}{2}\left\|\Omega_{3}\right\|_{2}^{2}+\sum_{j=i+1}^{n} \sum_{i=1}^{n} \frac{\eta_{i, j}}{2}\left\|\Theta_{i, j}\right\|_{2}^{2}+\frac{\tau}{2}\|\gamma\|_{2}^{2}$

D. 算法描述

具体的预测模型（SEA）总结如算法1和算法2。由于矩阵乘法和连接级嵌入，算法1的时间复杂度为 $\mathcal{O}\left(|\mathcal{V}|^{2}+|\mathcal{E}|\right)$ 。至于算法2，因为受到测试集中边的数量限制，其时间复杂度为 $\mathcal{O}\left(\left|\mathcal{E}^{*}\right|\right)$ ，

E. 带权图压缩

当图的大小过大时，处理连接级任务的计算成本可能会急剧增加。为了提高大型加权图上连接权重预测的效率，本文进一步提出了一种图压缩方案。通过图压缩过程，原始的可观察图 $\mathcal{G}^{o}=\left(\mathcal{V}, \mathcal{E}, \mathcal{W}-\mathcal{W}^{*}\right)$ 可以转变为一个较小的图 $\mathcal{G}_{c}^{o}=\left(\hat{\mathcal{V}}, \hat{\mathcal{E}}, \hat{\mathcal{W}}-\mathcal{W}^{*}\right)$ ，其中 $|\hat{\mathcal{V}}|<|\mathcal{V}| \text,|\hat{\mathcal{E}}|<|\mathcal{E}|$ 。需要注意的是，在恢复缺失的连接权重集合W∗时，必须在图压缩过程中保留相应的边集合E∗ ⊆ E。

图压缩的过程主要涉及三个基本操作，包括(1)节点合并，(2)自环，(3)边合并，为了实现(1)显著减少图中节点数量和(2)大部分保留连接权重信息。这三个基本操作的定义如下，示例图如下：

节点合并：给定一对连接的节点{u, v}，如果它们具有相同的节点度，即满足条件 $d_u=d_v$ ，那么这两个节点会合并成一个新的超级节点，标记为u或v。否则，如果 $d_u>d_v$ ，得到的超级节点只能标记为u，因为它的度较大，或者我们称节点u吞并了节点v。这两种情况都称为节点合并。

自环：当两个节点合并成为一个超级节点时，原始连接这两个节点的边会变成连接超级节点自身的边。这个过程称为自环。

边合并：当两个节点合并成为一个超级节点时，从另一个节点指向原始两个节点的两条边需要合并成为一条指向超级节点的超级边。同时，超级边的权重是原始两条边上权重的和。这个过程称为边合并。

在本文的问题设置中，由于连接的信息比节点的信息更重要，自环和边合并的操作有助于防止边信息的丢失，这将有利于在压缩图上对SEA进行建模。

为了避免局部压缩图形，必须确保图形尽可能均匀地被压缩。为此，提供了以下两个技巧：

1：每次选择具有较少共同邻居的节点对进行节点合并，这样会对图的局部结构的影响较小，因为需要较少的边合并操作。

2：如果图中的某个节点对已经包含一个超级节点，则不允许进一步压缩。这样，与超级节点相关联的图的局部区域不会过度压缩。

值得一提的是，为了确保图的压缩效率，当选择一个候选节点对进行合并时，可以简单地计算两个节点的度之和，而不是计算它们的共同邻居数。根据实证验证，一个度之和较小的节点对也能保证它们有较少的共同邻居。加权图压缩的详细步骤在算法3中描述。

此外，本文还对图压缩时的一些特定节点结构进行了对应的讨论及证明，感兴趣的读者可以参见正文。

基于前面所述的三个算法，可以得出完整模型实际上是一个两阶段的计算框架。在第一阶段，通过算法3对带有缺失连接权重的观察到的加权图进行压缩。在第二阶段，通过加权邻接矩阵重构，即算法1和2，恢复压缩图中的缺失连接权重。包含加权图压缩和压缩图重构（SEA）步骤的完整计算框架下图所示。

图中，左侧图表展示了一个观察图被压缩成一个较小图的情况，右侧图表展示了如何通过自注意机制将连接表示为嵌入向量。对于较小的网络，可以忽略第一阶段，直接将带有压缩的加权图应用于第二阶段。需要注意的是，由于节点合并引入了自连接边，因此方程中显示的损失函数需要稍作修改，如下所示：

$\mathcal{L}=\sum_{u, v} a_{u, v}\left(w_{u, v}^{\prime}-w_{u, v}\right)^{2}+\nu \sum_{u, v} a_{u, v}\left\|B_{u, v}-B_{v, u}\right\|_{2}^{2}+\mathcal{L}_{r e g}$

实验结果分析

A. 衡量指标

为了评估连接权重预测的有效性，本文选择RMSE来衡量模型的预测性能。RMSE能够计算缺失连接权重和预测连接权重之间的统计差异。例如，如果在测试集中有N个唯一连接的权重（w1、w2、...、wN），而从预测模型得到了相应的权重（w'1、w'2、...、w'N），那么可以使用以下公式来评估预测器的优劣：

$R M S E=\sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(w_{i}-w_{i}^{\prime}\right)^{2}}$

RMSE的值越小，预测准确度越高。

B. 数据集

本文使用数据集如下：

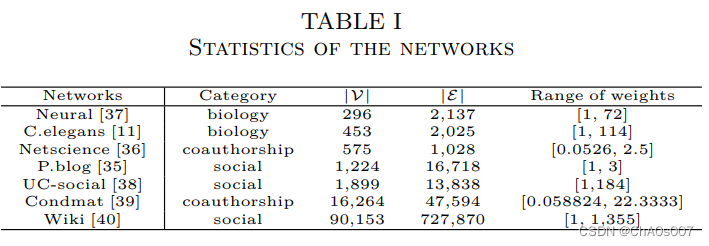
C. 模型参数设置

所提出的SEA模型的一些详细参数设置如下所述。从编码器中得出的每个嵌入向量具有128维度。为了应用广泛使用的Adam优化器，初始学习率设置为0.01，并且每100个epochs降低0.9倍。训练迭代的次数根据具体的数据集不同而设置不同。具体而言，对于Condmat和Wiki数据集，应用了100个训练epochs；对于P.blog数据集，应用了800个训练epochs；对于UC-social数据集，应用了500个训练epochs；对于其余数据集，应用了300个训练epochs。

在链接预测社区广泛采用的是本文中应用的"留出10%"评估模式。在链接权重预测中，随机选择原始网络中的10%链接权重作为测试集，保留90%链接权重的网络作为观测网络或训练网络。为避免由于一次性实验引起的评估偏差，每个结果都经过10次独立的训练网络和测试集的平均。用于实验的计算机是一台配备Intel i9-10900k 3.7GHz处理器，64G内存和Nvidia 3090 GPU的台式机。

D. 基准模型及对比结果

为了评估SEA模型的预测能力，我们选择了近年来提出的七种知名图表示模型进行比较，包括Deepwalk，Node2vec，Grarep ，SDNE ，LINE ，GAE 和VGAE。与其他五种图嵌入模型不同，GAE和VGAE是为属性网络设计的。为了使GAE和VGAE适用于普通加权图，我们使用加权邻接矩阵的第i列向量作为节点i的初始特征向量。由于上述七种图学习模型不能直接应用于连接权重预测，因此将获得的节点嵌入向量连接成边特征向量，然后进一步训练线性回归模型来评估它们在连接权重预测上的性能。此外，我们还选择了七种基于浅层特征的连接权重预测方法进行比较，包括三种可靠路径方法，三种线性图方法和NEW方法。所有基线模型的参数均根据原始文献进行设置。

对于Neural、C.elegans、Netscience和P.blog等小型网络，实验在未压缩的观察图上进行。对于UC-social、Condmat和Wiki等较大的网络，实验在压缩后的图上进行。需要注意的是，由于Wiki的规模过大，Wiki被压缩了十轮。

如上表所示，本文所提出的SEA在四个未压缩的小网络上均优于所有竞争基准。具体而言，在C.elegans和Netscience网络上，与第二好的方法相比，SEA的RMSE显著降低了19.35%和7.63%。对于压缩的图，SEA也在三个压缩网络上表现最佳。同样，SEA在UC-social和Condmat网络上的RMSE分别显著降低了3.89%和6.31%。值得注意的是，对于像LG-RF、LG-GBDT和LG-SVM这样基于线性图的方法，它们在计算基于中心性的度量时非常耗时，因此无法获得大型图（包括压缩后的图）的最终结果，例如Condmat和Wiki。

总结

在本文中提出了一个名为SEA的GNN框架，用于在普通加权图上进行连接权重预测。对七个真实世界网络（其中三个被压缩）的实验证明，该方法在RMSE指标上优于最先进的方法。为了解决在大型图上如何预测缺失连接权重的问题，我们特别提出了一种图压缩方法，能够有效地减小图的大小，并在很大程度上保留连接信息，从而保持了所提出的SEA模型的预测能力。有趣的是，我们发现全局聚类系数可以用作指标，预估所提出的图压缩方法将如何对压缩图上的预测结果产生影响。

与以前的研究相比，这项工作在使用GNN和图压缩技术研究普通图上的连接权重预测问题方面提供了一些新的见解。未来，我们认为有三个方向可能值得进一步探索：

(i) 目前，图压缩是所提出的计算框架的一个独立模块。如何将其整合到框架中，以实现端到端的训练，将是一个有趣的方向。

(ii) 同样有趣的是，是否可以将图压缩方法应用于更多类型的图，如有向图，以及更多的图挖掘任务，如传统的连接预测、节点分类和图异常检测。

(iii) 作为这项工作的扩展，如果将现有的网络作为训练网络，将新出现的连接作为测试集，那么所提出的模型可能适用于时态和演化网络上的连接权重预测。