论文笔记 | ICDE 2022 | Robust Attributed Network Embedding Preserving Community Information

本文链接：https://blog.youkuaiyun.com/ChA0s007/article/details/131540884

AnECI是一个鲁棒的网络嵌入框架，通过图卷积网络学习属性网络的非线性嵌入，并通过高阶模块度函数保留社区结构，提高对网络异常和攻击的抵抗力。这种方法不仅重构高阶接近度，还适用于有重叠社区的网络，通过实验显示在节点分类、异常检测和社区检测任务中表现出优越性能。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Robust Attributed Network Embedding Preserving Community Information

文章信息

[来源]：2022 IEEE 38th International Conference on Data Engineering (ICDE)

[作者]：Yunfei Liu∗, Zhen Liu∗, Xiaodong Feng, Zhongyi Li

[链接]：Robust Attributed Network Embedding Preserving Community Information | IEEE Conference Publication | IEEE Xplore

[代码]：https://github.com/Gmrylbx/AnECI

内容简介

近年来，涉及图上深度学习的方法如雨后春笋般涌现，其中图卷积网络（GCN）是一项重大进展。GCN可以增强网络嵌入结果的表示能力，对属性网络具有很强的适应性。图自编码器（GAE）和变分图自编码器（VGAE）由GCN编码器和重构解码器组成，用于捕捉高度非线性属性，在属性网络嵌入和下游任务中表现良好。此后，出现了一些更先进的方法，如AGE。然而，这些方法存在两个主要限制。

首先，本质上，这些网络嵌入方法主要关注网络的微观结构，新的嵌入空间中仅保留了每两个节点之间的成对连接或相似性。然而，在这些方法中，对于网络的中等结构描述——社区结构，很大程度上被忽视了。大多数网络由不同的社区组成，这些社区被视为一组节点，社区内部的连接密集，而社区之间的连接稀疏。因此，嵌入表示能否很好地反映社区结构是网络嵌入方法的关键要求，对于属性网络也同样重要。与微观结构的成对连接不同，社区结构在更高的结构层次上对节点表示施加了约束，即同一社区中的节点表示应该比属于不同社区的节点更相似。因此，将社区结构融入网络嵌入可以为解决成对连接的微观结构中数据稀疏性问题提供有效和丰富的信息，并且可以学习更具辨别力的节点表示。

其次，大多数基于深度学习的网络嵌入方法对网络攻击或节点污染非常脆弱。一些研究表明，节点的学习表示对微观结构的微小变化非常敏感，例如添加或删除边或节点，下游任务的性能，如节点分类或链接预测，会显著下降。这通常是过于强调从局部结构中的一阶接近度而忽视社区结构的结果。如果可以考虑社区成员资格的无监督信息来指导网络嵌入，结果将对攻击或节点污染具有鲁棒性。节点的社区归属作为全局结构信息，不会轻易受到网络结构中微小局部变化的影响。

基于上述观察，我们提出了一种名为保留社区信息的属性网络嵌入（AnECI）的鲁棒框架。首先，AnECI使用图卷积编码器通过图卷积操作传播属性信息，学习属性网络的非线性嵌入。其次，与基于成对连接的模型学习不同，我们提出了一种新的模块度函数，通过保留从数据本身学到的底层社区结构作为无监督学习来指导网络嵌入，以提高对局部网络异常或攻击的鲁棒性。此外，与传统基于网络一阶接近度和硬分区的社区结构定义的模块度函数不同，我们针对高阶接近度和重叠社区结构开发了一种新的模块度函数。此外，AnECI使用学习到的节点嵌入向量作为解码器来重构高阶接近度，这也与通常重构一阶邻接矩阵的传统方法不同。在存在轻微攻击或节点污染时，高阶接近度比一阶接近度更稳定，因为在计算两个节点之间的接近度时，它还考虑了更多全局信息。据我们所知，我们的工作是首次尝试将基于高阶接近度的社区模块度结合到网络嵌入中，并通过学习表示重新构建高阶接近度。我们在真实基准数据集上进行了大量实验，包括在干净和受攻击图上的节点分类、异常检测和社区检测任务，结果显示AnECI优于现有的属性网络嵌入方法。

本文主要贡献：

• 我们提出了AnECI，这是一个鲁棒的网络嵌入模型，增强了嵌入对抗性攻击的鲁棒性。据我们所知，这是首次研究这个具有挑战性的任务。

• 不同于传统的模块度函数只关注一阶接近度和基于硬划分的社区结构，我们提出了一种新的模块度函数，适用于高阶接近度和重叠社区结构。

• 使用大量的实验结果证明我们提出的方法在各种下游任务中的有效性。

Attributed Network Embedding preserving Community Information（保留社区信息的属性网络嵌入）

结构总览

• 使用图卷积网络的属性网络编码器。图卷积网络模块作为网络编码器，用于学习每个节点的非线性潜在嵌入。

• 通过高阶模块度函数进行社区保留。为了使节点在嵌入空间中对网络异常或攻击具有更强的鲁棒性，节点的表示应与社区结构相关联。这是通过使用模块度函数进行指导来实现的，假设属于同一社区的节点应具有较高的接近度。

• 高阶网络接近度重构。除了保留社区的中观结构外，学习到的节点嵌入还可以重构高阶成对接近度。

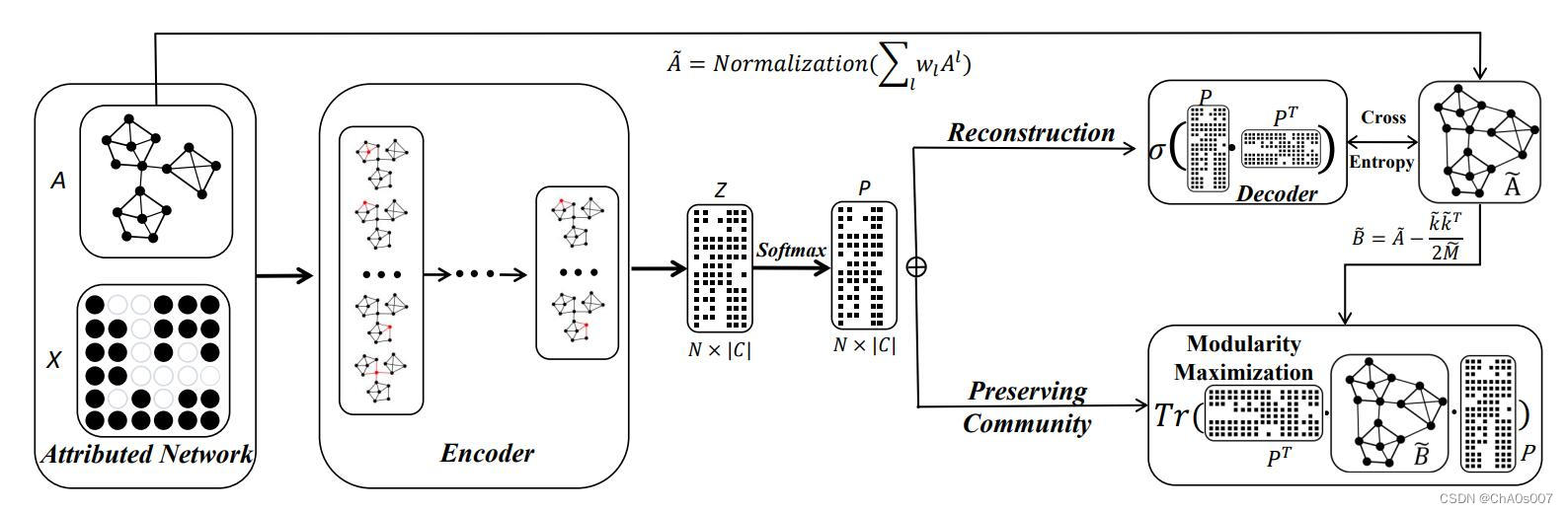
A. 图卷积编码器

本文受到图卷积网络（GCN）的启发，提出通过在网络上平滑传播属性信息和对输入属性进行非线性转换来对属性网络进行编码。它可以缓解节点之间观察到的连接之外的网络稀疏性问题。同时，通过多层非线性转换，捕捉到数据的非线性和属性网络上两种信息模态的复杂交互。具体而言，GCN将卷积操作扩展到频谱域的网络数据中，并通过频谱卷积函数学习一个新的潜在表示：

$H^{(l+1)}=\phi\left(H^{(l)}, A \mid W^{(l)}\right)=\phi\left(D^{-1 / 2} A D^{-1 / 2} H^{(l)} W\right)$

其中φ(·)是激活函数，如sigmoid和LeakyReLU。 $H^{(l)} \in \mathbb{R}^{N \times h^{l}}$ 和 $H^{(l+1)} \in \mathbb{R}^{N \times h^{l+1}}$ 是第(l+1)个卷积层的相应输入和输出。我们将特征矩阵 $H \in \mathbb{R}^{N \times d}$ 作为第一层的输入，即H(0) = X；最后一层的输出是学习到的嵌入矩阵，记为 $Z \in \mathbb{R}^{N \times h}$ 。

为了使每个节点的嵌入包含社区结构信息，如果我们将嵌入维度h设置为社区数目|C|，我们可以从学到的嵌入矩阵Z中推断出社区成员信息。通常，我们通过softmax映射将学习到的嵌入矩阵Z转换为社区成员概率矩阵P，使得每个元素介于0和1之间，并且每行元素之和为1，表示为：

$P=\operatorname{softmax}(Z), \text { where } p_{i}^{k}=\frac{e^{z_{i}^{k}}}{\sum_{j} e^{z_{i}^{j}}}$

B. 通过高阶模块度对社区结构进行建模

1）重新审视传统的模块度函数：作为最常用的方法之一，基于模块度最大化的社区检测用于构建社区结构，我们将首先重新审视传统的定义，将其扩展为高阶接近度和重叠社区结构。具体而言，给定一个网络接近度矩阵 A，这在传统方法中就是邻接矩阵，模块度函数定义为：

$Q=\frac{1}{2 M} \sum_{i, j}\left(A_{i j}-\frac{k_{i} k_{j}}{2 M}\right) \sigma\left(c_{i}, c_{j}\right),$

其中， $A_{ij}$ 可以理解为两个节点 $v_i$ 和 $v_j$ 之间的观察到的结构信息，即节点 $v_i$ 和 $v_j$ 之间的边； $k_{i} k_{j} /(2 M)$ 表示如果边是随机放置的情况下，这两个节点之间的预期结构信息，其中 $k_i$ 表示节点 $v_i$ 的度。 $c_i$ 、 $c_j$ 分别表示节点 $v_i$ 和 $v_j$ 的社区标签， $\sigma\left(c_{i}, c_{j}\right)$ 表示它们是否属于同一个社区，即如果 $c_i$ = $c_j$ ，则 $\sigma\left(c_{i}, c_{j}\right)$ =1，否则为0。因此，模块度直观地衡量了社区内部边的数量与等价网络中随机放置边的预期数量之间的差异。模块度值越大，社区内部包含的结构信息与预期值的差异越大，反映出网络的社区结构更加紧密。

定义一个模块度矩阵 $B=\left\{B_{i j}\right\} \in \mathbb{R}^{N \times N}$ ，其中每个元素 $B_{i j}=A_{i j}-k_{i} k_{j} /(2 M)$ ，模块度可以用矩阵形式重新表示

$Q=\frac{1}{2 M} \operatorname{tr}\left(P^{T} B P\right), \text { s.t. } \operatorname{tr}\left(P^{T} P\right)=N$

其中，'tr(·)'表示方阵·的迹，定义为对角元素之和； $P \in \mathbb{R}^{N \times|\mathcal{C}|}$ 是社区成员指示矩阵。在传统的硬分区社区结构定义中，每个行向量 $p_i$ 是一个one-hot编码向量，表示只有一个元素为1，其余元素都为0，满足约束条件 $tr(P^T P) = N$ 。

2）广义模块性函数：上述的模块性定义仅强调了一阶近邻关系，并且仅适用于基于硬分区的社区结构。为了扩展为广义情景，即基于高阶近邻关系或重叠社区结构的软权重情况，我们首先提出以下模块性函数：

$\tilde{Q}=\frac{1}{\lambda} \sum_{c_{k} \in \mathcal{C}} \sum_{i, j}\left[\gamma_{i, j, c_{k}}^{o} E_{i, j}^{o}-\gamma_{i, j, c_{k}}^{e} E_{i, j}^{e}\right],$

其中， $E_{i j}^{o}$ 和 $E_{i j}^{e}$ 可以分别理解为节点 $v_i$ 和 $v_j$ 之间观察到的和期望的结构信息的广义形式。 $\gamma_{i, j, c_{k}}^{o}$ 和 $\gamma_{i, j, c_{k}}^{e}$ 是相应的调整因子，衡量节点vi和vj之间的结构信息对社区 $c_k$ 的影响。具体而言，它们是 $\alpha_{i, c_{k}}$ 和 $\alpha_{j, c_{k}}$ 的非递减函数，分别表示节点 $v_i$ 和 $v_j$ 对社区 $c_k$ 的权重，如下所示：

$\begin{aligned} \gamma_{i, j, c_{k}}^{o} & =\mathcal{F}^{o}\left(\alpha_{i, c_{k}}, \alpha_{j, c_{k}}\right) \in[0,1] \\ \gamma_{i, j, c_{k}}^{e} & =\mathcal{F}^{e}\left(\alpha_{i, c_{k}}, \alpha_{j, c_{k}}\right) \in[0,1] \end{aligned}$

其中，

$\alpha_{i, c_{k}} \in[0,1], \sum_{c_{k} \in \mathcal{C}} \alpha_{i, c_{k}}=1$

直观上， $\gamma_{i, j, c_{k}}^{o}$ 和 $\gamma_{i, j, c_{k}}^{e}$ 应满足以下两个等价条件：

$\begin{array}{l} \gamma_{i, j, c_{k}}^{o}=\gamma_{i, j, c_{k}}^{e}=0, \operatorname{IFF}\left(\alpha_{i, c_{k}}=0 \| \alpha_{j, c_{k}}=0\right) ; \\ \gamma_{i, j, c_{k}}^{o}>0, \gamma_{i, j, c_{k}}^{e}>0, \operatorname{IFF}\left(\alpha_{i, c_{k}}>0 \& \alpha_{j, c_{k}}>0\right) . \end{array}$

在传统的基于一阶接近性的定义中λ = 2M； $E_{i j}^{o}$ 和 $E_{i j}^{e}$ 确切对应于 $A_{ij}$ 和 $k_{i} k_{j} /(2 M)$ ； $\gamma_{i, j, c_{k}}^{o}$ 和 $\gamma_{i, j, c_{k}}^{e}$ 由 $\sigma\left(c_{i}, c_{j}, k\right)$ 度量；如果节点 $v_i$ 和 $v_j$ 属于同一个社区，则 $\sigma\left(c_{i}, c_{j}, k\right)=1$ ，否则为0。在接下来的两个小节中，我们将展示如何设计基于高阶接近性的社区划分和重叠社区结构的新 $\left(E_{i j}^{o}, E_{i j}^{e}\right)$ 和 $\left(\gamma_{i, j, c_{k}}^{o}, \gamma_{i, j, c_{k}}^{e}\right)$ 。

3）拓展高阶接近性的模块度：对于具有社区结构的网络，同一社区中的许多节点通常不直接通过边相连。将两个节点归为同一社区通常是因为它们之间存在高阶接近性，即它们可能直接连接到另一个中间节点。因此，基于一阶接近性的社区只能表示简单的结构，但在现实生活中，结构往往更为复杂。而且，仅仅使用传统一阶模块度函数导出的社区标签来指导节点表示学习会容易受到异常值或攻击的影响，即不够鲁棒。因此，我们提出将模块度函数从一阶接近性拓展到高阶结构信息。

因此， $E_{i j}^{o}$ 和 $E_{i j}^{e}$ 的定义可以拓展到高阶接近性。由于 $A_{ij}^l$ 计算的是从节点 $v_i$ 到节点 $v_j$ 的l跳路径数，描述了这两个节点之间的 $l$ 阶接近性， $A_{ij}^l$ 在所有 $ls$ 上的和，即 $\tilde{A}_{i j}$ ，可以定义为总体观察到的高阶结构信息 $E_{i j}^{o}$ 。类似地， $\tilde{k}_{i} \tilde{k}_{j} /(2 \tilde{M})$ 可以表示两个节点之间的期望高阶结构信息 $E_{i j}^{e}$ ，其中 $\tilde{k}_{i}=\sum_{j} \tilde{A}_{i j}$ 可以看作节点vi的高阶结构度，而 $\tilde{M}=\sum_{i, j} \tilde{A}_{i j}$ 是所有高阶结构度的总和。因此，新的模块度 $\tilde{Q}$ 的定义如下：

$\tilde{Q}=\frac{1}{2 \tilde{M}} \sum_{i, j}\left[\tilde{A}_{i j}-\tilde{k}_{i} \tilde{k}_{j} /(2 \tilde{M})\right] \sigma\left(c_{i}, c_{j}\right)$

4）拓展重叠社区的模块度：在传统的模块度函数中，社区结构是一种硬分区的方式，即每个节点只属于一个社区。然而，由于复杂的网络结构，社区的成员之间紧密相连，导致节点和属性在多个社区之间存在一些相似性。另一方面，真实的复杂网络从未被分割成清晰的子网络，特别是由社交互动形成的网络。例如，演员通常属于许多不同的社区，同时参与多个群体的活动。在本节中，我们尝试通过定义 $\gamma_{i, j, c_{k}}^{o}$ 和 $\gamma_{i, j, c_{k}}^{e}$ 来将其拓展为带有软权重的重叠社区结构。

在提出我们的想法之前，我们首先提出了以下两个拓展函数应符合的属性：

• 属性1. 为保持普适性，为重叠社区结构定义的模块度函数应退化为基于硬分区的常规模块度函数。

• 属性2. 为重叠社区定义的模块度函数应暗示一个节点属于不同社区的不同概率。

为了符合属性1，应满足以下规则，即当相应的两个节点仅属于同一社区 $c_k$ 时， $\gamma_{i, j, c_{k}}^{o}$ 和 $\gamma_{i, j, c_{k}}^{e}$ 都应达到1。

为了满足以上属性，本文定义 $\gamma_{i, j, c_{k}}^{e}=\gamma_{i, j, c_{k}}^{o}=\mathcal{F}\left(\alpha_{i, c_{k}}, \alpha_{j, c_{k}}\right)$ ，本文设置 $\mathcal{F}\left(\alpha_{i, c_{k}}, \alpha_{j, c_{k}}\right)=\alpha_{i, c_{k}} \alpha_{j, c_{k}}$ 。本文提出满足以上属性的模块度函数的定义如下：

$\tilde{Q}=\frac{1}{2 \tilde{M}} \sum_{c_{k} \in \mathcal{C}} \sum_{i, j} \alpha_{i, c_{k}} \alpha_{j, c_{k}}\left[\tilde{A}_{i j}-\frac{\tilde{k}_{i} \tilde{k}_{j}}{2 \tilde{M}}\right]$

矩阵格式可以改写为

$\tilde{Q}=\frac{1}{2 \tilde{M}} \operatorname{tr}\left(P^{T} \tilde{B} P\right)$

其中，P是通过属性网络编码器获得的社区成员关系矩阵，其中 $p_i^k$ 正好是对应的权重 $\alpha_{i, c_{k}}$ ； $\tilde{B}_{i j}=\tilde{A}_{i j}-k_{i} \tilde{k}_{j} /(2 \tilde{M}) \text {. }$

C.高阶接近度重构解码器

在本小节中，我们将展示如何通过属性网络编码器模块的输出来重构原始网络结构。首先，我们将尝试重构 $\tilde{A}$ ，而不是GAE/VGAE 中的邻接矩阵A，因为高阶接近度在计算接近度时考虑了更多的全局信息，在存在轻微攻击或节点污染时更加稳定和鲁棒。此外，我们利用社区成员矩阵P而不是嵌入矩阵Z来重构图结构，因为我们假设在高阶空间中，共享相似社区成员的两个节点更有可能相连，这进一步通过社区结构增强了节点嵌入。在数学上，解码器将潜在嵌入P作为输入，并预测每对节点之间的高阶接近度：

$\hat{A}_{i j}=\operatorname{sigmoid}\left(p_{i} p_{j}^{T}\right)$

其中， $\hat{A}_{i j}=p_{i} p_{j}^{T}$ 衡量了与节点 $v_i$ 和 $v_j$ 对应的成员向量 $p_i$ 和 $p_j$ 之间的相似性，两个节点之间的相似性越高，它们在高阶空间中相连的概率也越高。因此， $\hat{A}_{i j}$ ∈ [0, 1] 可以被视为节点 $v_j$ 在高阶空间中与节点 $v_i$ 完全连接的估计概率。结合前面对归一化 $\hat{A}_{i j}$ 的定义，我们可以推导出两个二项概率分布，即 $\left[\tilde{A}_{i j}, 1-\tilde{A}_{i j}\right]$ 和 $\left[\hat{A}_{i j}, 1-\hat{A}_{i j}\right]$ ，其中 $1-\tilde{A}_{i j}$ 和 $1-\hat{A}_{i j}$ 分别表示对应的两个节点在高阶空间中完全断开连接的真实或估计概率。因此，这两个分布之间的差异可以用于检测网络上的结构异常或攻击。换句话说，如果解码器能够高度重构两个节点之间的高阶接近性，则嵌入空间Z中对应的两个向量将很好地编码这些结构信息。形式上，高阶接近性重构解码器的损失可以通过对每对节点应用广义交叉熵的总和来定义，如下所示：

$L_{R}=-\sum_{i . j}\left(\tilde{A}_{i j} \log \left(\hat{A}_{i j}\right)+\left(1-\tilde{A}_{i j}\right) \log \left(1-\hat{A}_{i j}\right)\right)$

D.鲁棒的属性网络表示

到目前为止，我们已经介绍了如何通过GCN模块对属性网络进行编码，如何通过新的模块化函数保持社区结构，以及如何通过解码器重建高阶接近性。为了共同学习潜在表示Z，我们提出的AnECI的总目标函数可以被表述为：

$\min _{W} \mathcal{L}=-\beta_{1} \tilde{Q}+\beta_{2} L_{R}$

其中，β1和β2是平衡社区结构和高阶接近性重建贡献的超参数。通过最小化上述目标函数，我们提出的鲁棒图卷积自编码器可以迭代地逼近基于嵌入的潜在表示的输入属性网络，这可以用于下游任务。

实验分析

A 节点分类

对于所有无监督图嵌入方法，我们使用节点嵌入作为输入特征，在训练集上训练逻辑回归分类器，并在测试集上报告平均准确率（及标准差）。如下表所示，AnECI在三个数据集上表现最好，仅在Citeseer上略逊于GAT和DGI。具体而言，与无监督方法相比，AnECI能够使准确率相对于最佳基线DGI分别提高9.4%和2.4%。这些改进表明保留底层社区信息是有益的。令人惊讶的是，AnECI的结果甚至在大多数情况下超过了半监督模型。我们认为这些令人鼓舞的结果源于AnECI间接允许每个节点适应底层社区结构的事实，通过加强同一社区中节点之间的关系，削弱不同社区节点之间的关系。

B 防御对抗攻击

在本节中测试了在三种不同类型对抗性攻击下的防御性能。论文原文中还对AnECI为何对攻击具有鲁棒性做出了进一步的解释，篇幅原因本文不再赘述，感兴趣读者可翻阅原文查看。

在测试全局攻击时，我们将扰动率δ从0增加到0.5，间隔为0.02，并在下图中报告相应的防御得分。结果显示，我们的模型在所有扰动率下都具有最高的防御得分，这是由于在无监督模型学习中保留了社区信息。这意味着社区是一个相对稳定的结构，不容易受到虚假边攻击的影响，因此无监督学习信号可以在嘈杂的环境中保持稳健性。然而，基于Skip-Gram的图嵌入方法（如LINE），则更注重维护嵌入的一阶接近性，而DGI和GAE都严重考虑成对连接。因此，虚假边对模型学习产生的影响与正常边相同，导致学习过程受到结构扰动的误导。其中防御得分定义如下：

$D S(\delta)=\sum_{e \in \mathcal{E}^{*}} s(e) /\left(\delta \sum_{e \in \mathcal{E}} s(e)\right)$

其中 $s\left(e_{i, j}\right)=1-\left(z_{i}^{T} z_{j} /\left(\left\|z_{i}\right\|\left\|z_{j}\right\|\right)\right)$ ， $e_{i, j} \in \mathcal{E}^{*} \cup \mathcal{E}$ ， $\mathcal{E}^{*}$ 表示被污染的边集合。

以下是在目标攻击及全局攻击下的防御效果：

C 异常检测

在异常检测任务中，我们对每个图像总共植入5％的异常节点。在获得节点i的嵌入zi后，令 $p_{i}=\operatorname{softmax}\left(z_{i}\right)$ ，其中 $p_{i} \in R^{|\mathcal{C}|}$ 表示社区成员向量。我们计算pi的异常分数如下：

$A \operatorname{Score}(i)=\sum_{k=1}^{|\mathcal{C}|} \frac{p_{i}^{k}}{p_{i}^{*}}, p_{i}^{*}=\max \left(p_{i}^{1}, p_{i}^{2}, \cdots, p_{i}^{|\mathcal{C}|}\right)$

异常检测结果如下：

该图表示AnECI和基准方法的异常检测结果（AUC）。注意，“S”、“A”和“S&A”分别表示具有结构异常、属性异常和结合异常的节点；“Mix”表示上述每种异常节点的1/3植入。

D 社区检测

总结

为了减轻网络异常值和对网络嵌入的网络攻击的影响，本文提出了一种保留社区信息的鲁棒属性网络嵌入方法（AnECI）。AnECI不同于传统的基于成对连接的方法，而是通过一个模块度函数来引导GCN编码器的网络嵌入，该函数根据嵌入本身决定并保留社区结构信息，以无监督的方式进行操作。它试图提高对常见的局部网络异常值或攻击的鲁棒性，因为它以无监督的方式考虑了全局社区结构。此外，AnECI通过重建高阶接近度来提高鲁棒性，当出现轻微的攻击或节点污染时，高阶接近度比一阶接近度更具鲁棒性，因为它考虑了更多的全局信息。本文在四个真实数据集上进行了大量实验，针对三个图挖掘任务，结果显示AnECI在方法方面取得了显着的进展。